Содержание
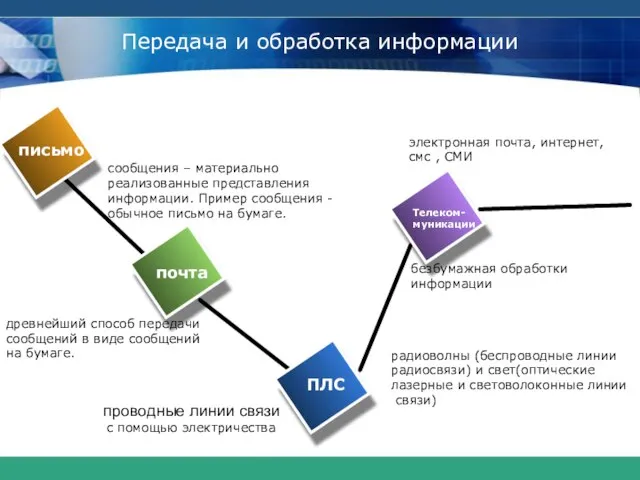
- 2. Передача и обработка информации радиоволны (беспроводные линии радиосвязи) и свет(оптические лазерные и световолоконные линии связи) проводные
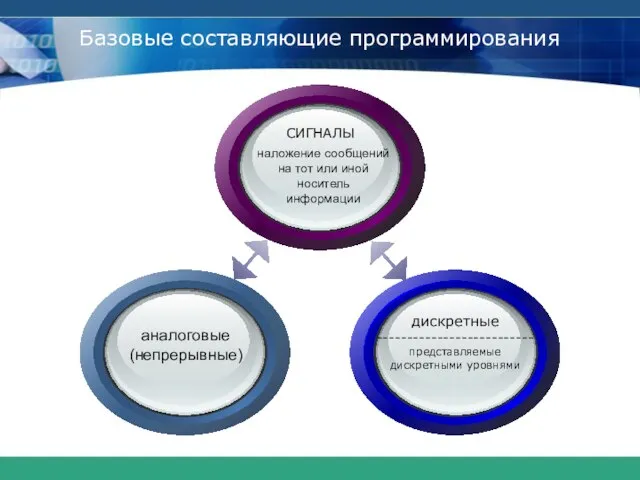
- 3. Базовые составляющие программирования наложение сообщений на тот или иной носитель информации аналоговые (непрерывные)
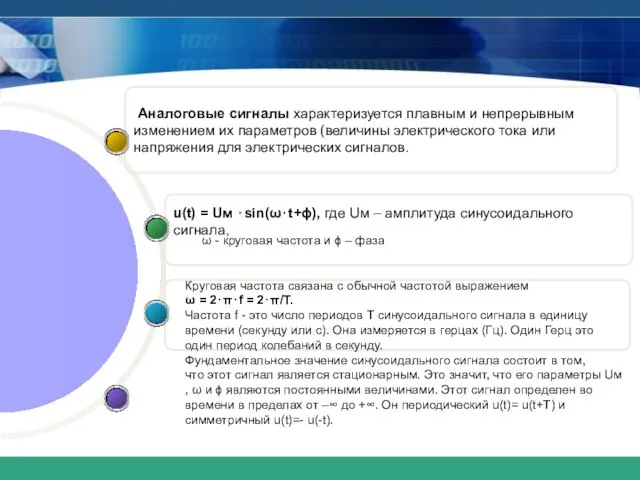
- 4. u(t) = Uм ⋅sin(ω⋅t+ϕ), где Uм – амплитуда синусоидального сигнала, Аналоговые сигналы характеризуется плавным и непрерывным
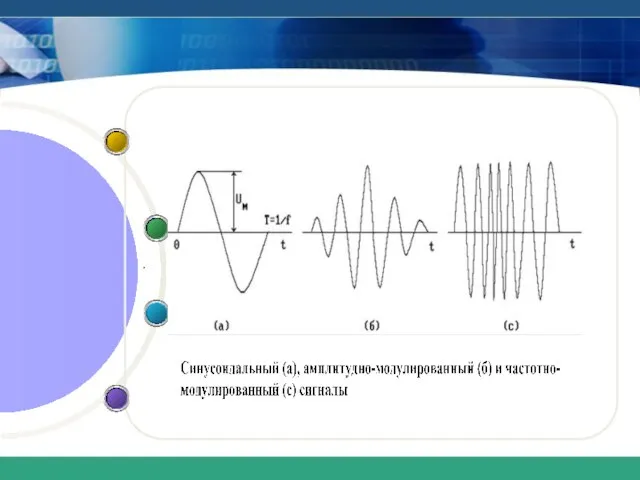
- 5. .
- 6. Дискретные и цифровые сигналы Дискретные сигналы - это сигналы, которые можно представить дискретными уровнями их параметров.
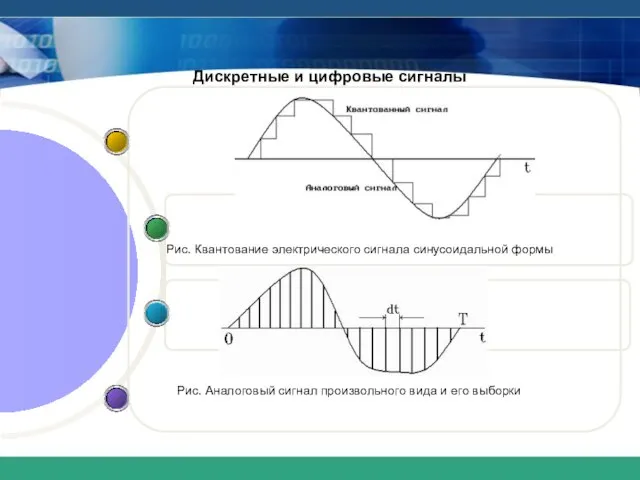
- 7. Дискретные и цифровые сигналы Рис. Квантование электрического сигнала синусоидальной формы Рис. Аналоговый сигнал произвольного вида и
- 8. Дискретные и цифровые сигналы В общем случае производят выборку (вырезку) сигналов в определенные моменты времени (рис.
- 9. Дискретные и цифровые сигналы Преобразование аналоговой информации в цифровую позволяет использовать мощные средства компьютерной обработки информации.
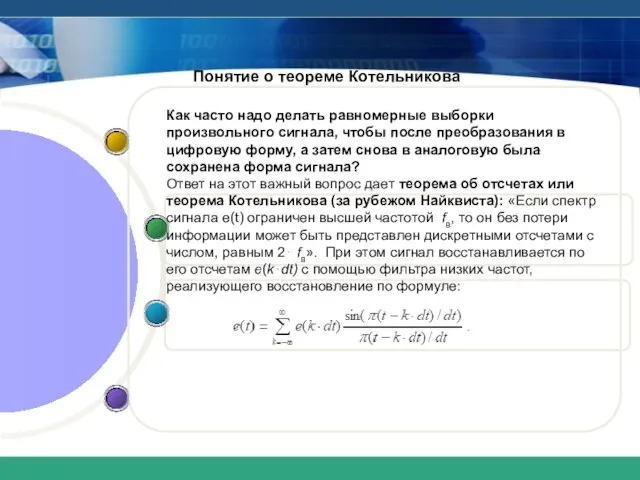
- 10. Понятие о теореме Котельникова Как часто надо делать равномерные выборки произвольного сигнала, чтобы после преобразования в
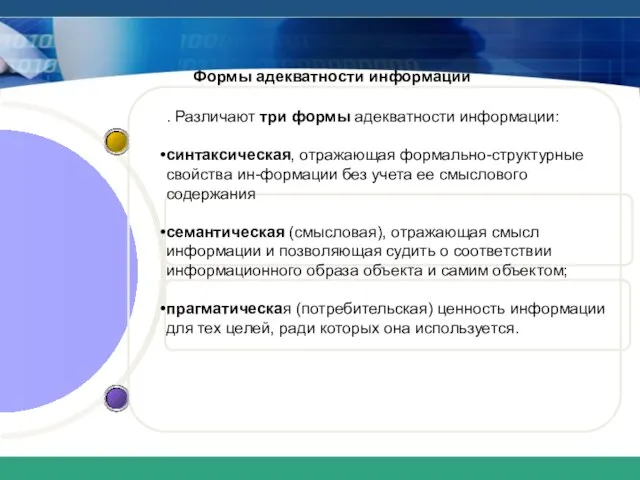
- 11. Формы адекватности информации . Различают три формы адекватности информации: синтаксическая, отражающая формально-структурные свойства ин-формации без учета
- 12. Синтаксическая мера информации – бит и байт Синтаксическая форма адекватности информации характеризуется объемом данных и количеством
- 13. Синтаксическая мера информации – бит и байт По мере роста объема передаваемой информации пришлось перейти к
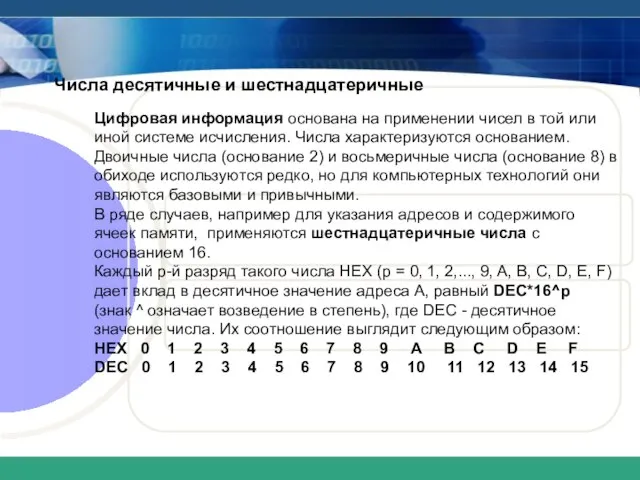
- 14. Числа десятичные и шестнадцатеричные Цифровая информация основана на применении чисел в той или иной системе исчисления.
- 15. Мера информации по Шеннону Допустим, что до получения информационного сообщения пользователь информационной системой имел предварительные (априорные)
- 16. Мера информации по Шеннону Пусть некоторая информационная система имеет N возможных состояний. Крупный специалист в информатике
- 17. Мера информации по Шеннону Заметим, что N = mn, где m – основание системы исчисления, n
- 18. Семантическая и прагматическая меры информации Для измерения смыслового (семантического) количества информации используется тезаурус – совокупность сведений,
- 19. Семантическая и прагматическая меры информации Отношение количества семантической информации Is к объему данных Vd принято называть
- 20. Что было до появления ЭВМ Первый проект механической машины, управляемой по введенной в нее с перфокарт
- 21. Что было до появления ЭВМ Так что Бэббиджа можно считать первым архитектором вычислительных машин – архитектура
- 22. Что было до появления ЭВМ Создание первых механических вычислительных устройств способствовало развитию теории вычислений и алгоритмов.
- 23. Что было до появления ЭВМ В 1896 году Холлерит создал фирму Computing Tabulation Company, которая занималась
- 24. Что было до появления ЭВМ Немецкий инженер Конрад Цузе на рубеже тридцатых/сороковых годов 20 века создал
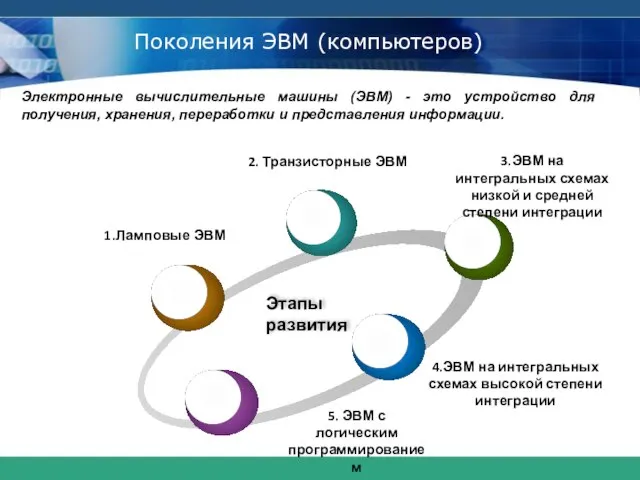
- 25. Поколения ЭВМ (компьютеров) Этапы развития 2. Транзисторные ЭВМ 4.ЭВМ на интегральных схемах высокой степени интеграции 1.Ламповые
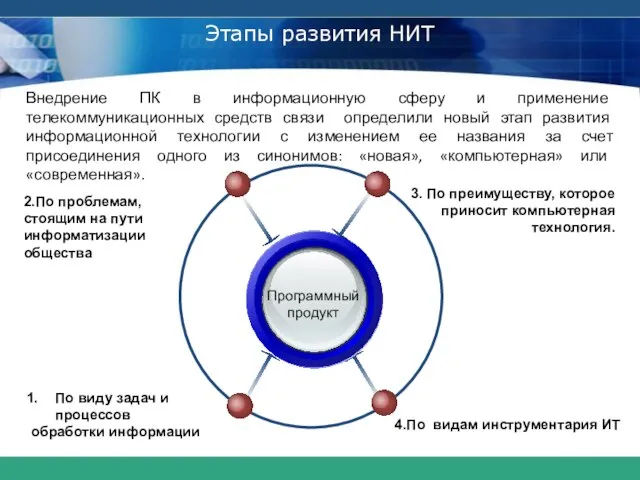
- 26. Новая информационная технология (НИТ)
- 27. Программный продукт 3. По преимуществу, которое приносит компьютерная технология. 2.По проблемам, стоящим на пути информатизации общества
- 28. Концепция НИТ Можно выделить две стратегии внедрения НИТ в локальную информационную структуру: 1.ИТ приспосабливается к условиям
- 30. Скачать презентацию

















 Статистическая обработка данных
Статистическая обработка данных Программирование циклов. Оператор for
Программирование циклов. Оператор for Макет версии №1
Макет версии №1 Поиск информации в интернете. 11 класс
Поиск информации в интернете. 11 класс Носители информации 3 класс
Носители информации 3 класс Проект Фабрика согласия (пропаганда и цензура)
Проект Фабрика согласия (пропаганда и цензура) Project information
Project information Понятие как форма мышления. Урок 12
Понятие как форма мышления. Урок 12 Программирование на языке C++
Программирование на языке C++ Стриминг через ключ трансляции
Стриминг через ключ трансляции Введение в программирование
Введение в программирование Занятие №4
Занятие №4 2_Osnovy_nauchnykh_issledovanii_774_ZFO
2_Osnovy_nauchnykh_issledovanii_774_ZFO Компьютерная графика. 7 класс
Компьютерная графика. 7 класс Кодирование информации. Ключевые слова
Кодирование информации. Ключевые слова Cirras & Drawing conversion project
Cirras & Drawing conversion project Программная работа лр 130305 01 сд.уп.04 09 12
Программная работа лр 130305 01 сд.уп.04 09 12 Работа с изображениями
Работа с изображениями Текстовый редактор. Программа с помощью которой можно подготовить и распечатать текстовые данные
Текстовый редактор. Программа с помощью которой можно подготовить и распечатать текстовые данные Презентация11
Презентация11 Структурный подход к моделированию систем. Методология функционального моделирования IDEF0
Структурный подход к моделированию систем. Методология функционального моделирования IDEF0 Примеры пользы от приоритезации доступа к вычислительным ресурсам в реальной жизни (а не только в ЦОДах)
Примеры пользы от приоритезации доступа к вычислительным ресурсам в реальной жизни (а не только в ЦОДах) Аниме. Игра
Аниме. Игра Оператор присваивания. Лекция №3
Оператор присваивания. Лекция №3 Элементы алгебры логики. Математические основы информатики
Элементы алгебры логики. Математические основы информатики Внутренняя память компьютера
Внутренняя память компьютера Компьютерная графика
Компьютерная графика +16 Архитектура ПК
+16 Архитектура ПК