Понятие алгоритма. Свойства алгоритма. Основные сведения об алгоритмах

алгоритм
исполнитель алгоритма
свойства алгоритма
дискретность
детерминированность
понятность
результативность
конечность
массовость
вычислительный процесс
сложность алгоритма

Художник Василий Тропинин «Золотошвейка» (1826)
понимает смысл алгоритма, может его корректировать и изменять, а также отказаться выполнять
одну и ту же команду выполняет каждый раз по-разному
неформальный исполнитель сам отвечает за свои действия
в роли неформального исполнителя чаще всего выступает человек
Исполнитель алгоритма
Исполнитель алгоритма – это субъект или устройство, способные правильно интерпретировать описание алгоритма и выполнить со­держащийся в нём перечень действий.
!
не размышляет над выпол­няемыми командами, а строго следует пошаговым инструк­циям алгоритма
одну и ту же команду всегда выполняет одинаково
за действия формального исполни­теля отвечает управ­ляющий им объект
в роли формального исполни­теля чаще всего выступает техническое устройство
Неформальный
исполнитель
Формальный
исполнитель

Понятие алгоритма
Алгоритм – точная система предписаний, определяю­щая содержание и порядок действий исполнителя над некоторыми объектами (исходными и промежуточными данными) для получения искомого результата за конечное число шагов.
!
ПРИМЕРЫ АЛГОРИТМОВ
Закрыть
входную дверь ключом
Нахождение n первых простых чисел
(метод Эратосфена)
Построение перпендикуляра
к прямой

Пример 1
Исполнитель: человек
Объекты алгоритма: ключ, дверь
Алгоритм
«Закрыть входную дверь ключом»
Вставить ключ в замочную скважину.
Повернуть ключ два раза на 180 градусов против часовой стрелки.
Вынуть ключ из замочной скважины.

Пример 2
Алгоритм «Нахождение всех простых чисел не больше заданного числа n по методу Эратосфена»
Выписать подряд все целые числа от 2 до n (2, 3, 4, …, n).
Присвоить переменной p значе­ние 2 (2 – первое простое число).
Зачеркнуть в списке числа, кратные p: 2p, 3p, 4p, …
Найти первое незачёркнутое число в списке, большее чем p, и прис­воить p соответствующее значение.
Повторять шаги 3 и 4, пока возможно (пока p2 ≤ n).
Незачёркнутые числа и есть все простые числа от 2 до n.
Простые числа от 2 до 100
Выполнить
2
3
5
7
11
13
17
19
23
29
31
37
41
43
47
53
59
61
67
71
73
79
83
89
97

Пример 2
Алгоритм «Нахождение всех простых чисел не больше заданного числа n по методу Эратосфена»
Простые числа от 2 до 100
p = 2
p = 3
p = 5
p = 7
Выписать подряд все целые числа от 2 до n (2, 3, 4, …, n).
Присвоить переменной p значе­ние 2 (2 – первое простое число).
Удалить из списка числа, кратные p: 2p, 3p, 4p, …
Найти первое число в списке, большее чем p, и прис­воить p соответствующее значение.
Повторять шаги 3 и 4, пока возможно (пока p2 ≤ n).
Оставшиеся числа и есть все простые числа от 2 до n.

Пример 3
Алгоритм «Построение перпендикуляра к прямой, проходящей через заданную точку O, лежащую на прямой с помощью циркуля и линейки»
Выполнить
Провести окружность с центром в точке O и радиусом 1 см.
Обозначить точки пересечения окружности с прямой: левую - A, правую - B.
Провести окружность с центром в точке A и радиусом равным AB.
Провести окружность с центром в точке В и радиусом равным AB.
Обозначить точки пересечения окружностей: верхнюю - C, нижнюю - D.
Провести прямую СD.

Пример 3
Алгоритм «Построение перпендикуляра к прямой, проходящей через заданную точку O, лежащую на прямой с помощью циркуля и линейки»
О
А
В
С
D
Провести окружность с центром в точке O и радиусом 1 см.
Обозначить точки пересечения окружности с прямой: левую - A, правую - B.
Провести окружность с центром в точке A и радиусом равным AB.
Провести окружность с центром в точке В и радиусом равным AB.
Обозначить точки пересечения окружностей: верхнюю - C , нижнюю - D.
Провести прямую СD.

Свойства алгоритма
Дискретность
Детерминированность
Понятность
Результативность
Массовость
Дискретность
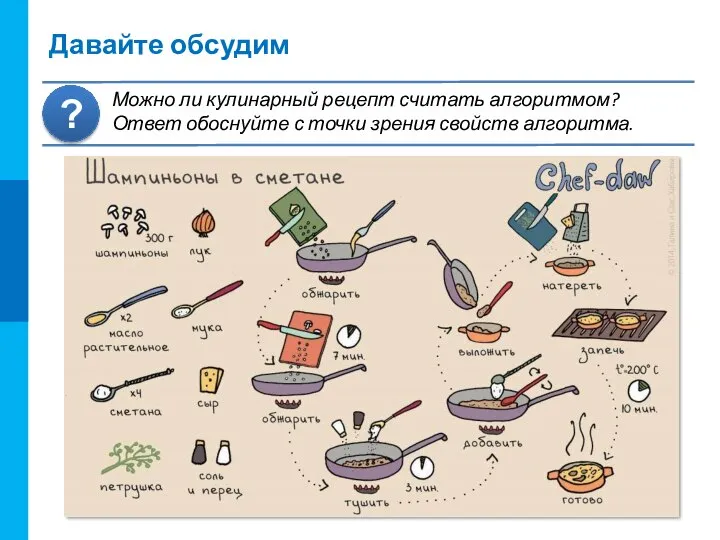
Выполнение алгоритма разбивается на последовательность законченных дейст­вий-шагов. Только выполнив одно действие, можно приступать к выполнению следующего. Произвести каждое отдельное действие исполнителю предписывает специальное указание в записи алгоритма – команда.
Детерминированность
Каждая команда алгоритма определяет однозначное действие исполнителя, и недвусмысленно указывает, какая команда должна выполняться следую­щей. Многократное выполнение алго­ритма при одном и том же наборе входных данных, дает одинаковые промежуточные и выходной результаты.
Понятность
Алгоритм не должен содержать предписаний, смысл которых может восприниматься исполнителем неодно­знач­но, т. е. запись алгоритма должна быть настолько чёткой и полной, чтобы у исполнителя не возникло потребности в принятии каких-либо самостоятельных решений.
Результативность
При точном исполнении команд алгоритма процесс должен прекратиться за конеч­ное число шагов, и при этом должен быть получен ответ на вопрос задачи. В качестве одного из возможных ответов может быть установление того факта, что задача решений не имеет.
Массовость
Алгоритм пригоден для решения любой задачи из некоторого класса задач, т. е. алгоритм правильно работает на неко­тором множестве исходных данных, которое называется областью примени­мости алгоритма.
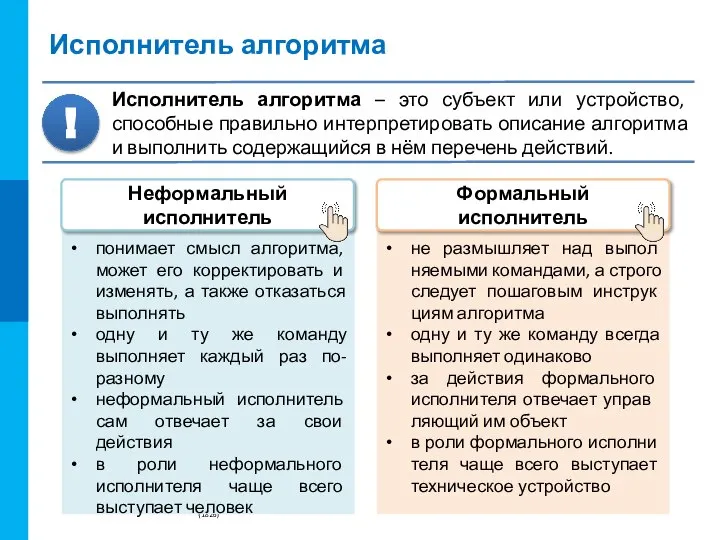
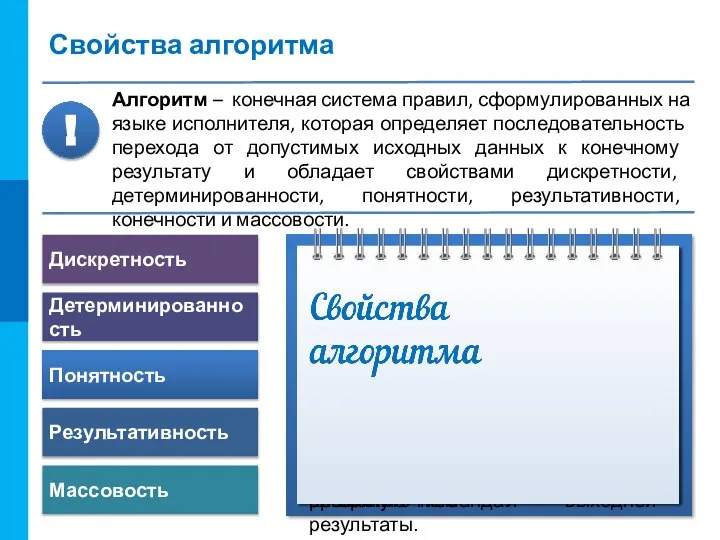
Алгоритм – конечная система правил, сформулированных на языке исполнителя, которая определяет последовательность перехо­да от допустимых исходных данных к конечному результату и обла­дает свойствами дискретности, детерминированности, понятности, результативности, конечности и массовости.
!

Давайте обсудим
Можно ли кулинарный рецепт считать алгоритмом?
Ответ обоснуйте с точки зрения свойств алгоритма.
?

Способы записи алгоритмов
словесная запись алгоритма
на естественном языке
запись алгоритма на языке программирования
с помощью блок-схемы –
стандартных графических объектов
(геометрических фигур)
запись алгоритма с помощью
формул, рисунков, таблиц
Сложение смешанных дробей
Привести дробные части чисел к наименьшему общему знаменателю.
Сложить только целые части.
Отдельно сложить дробные части.
Сложить результаты, полученные в п.2 и п. 3.
Если при сложении дробных частей получилась неправильная дробь, выделить целую часть из этой дроби и прибавить к полученной целой части.
Сократить полученную дробь.
Нахождение максимума
из 10 целых чисел
Нахождение НОД
Program NOD;
var a, b, n: integer;
Begin
writeln ('Введите два числа: ');
readln (a, b);
while a <> b do
if a>b then a := a - b
else b := b – a;
n:= a;
writeln ('НОД = ', n);
End.
Шахматный этюд
Мат в два хода.
Белые начинают и выигрывают
№
Белые
Черные
1
Ф f1-a1
K h8-g8
2
Ф a1-a8
№
Белые
Черные
1
Ф f1-a1
g6-g5
2
K f6-f7
№
Белые
Черные
1
Ф f1-a1
С h7-g8
2
K f6-g6
Решение:

Правила выполнения блок-­схем, внешний вид графических блоков и их назначение определяются стандартом ГОСТ 19.701–90 (ИСО 5807–85) «Схемы алгоритмов, программ, данных и систем. Обозначения условные и правила выполнения».
Блок-схема

Понятие сложности алгоритма
Теория алгоритмов предоставляет аппарат анализа различных алгоритмов решения одной и той же задачи, на основе которого можно выбрать самый эффективный (наилучший) алгоритм.
Вычислительным процессом, порождённым алгоритмом, называется последовательность шагов алгоритма, пройденных при его ис­полнении.
Сложность алгоритма – количество элементарных шагов (действий) в вычислительном процессе этого алгоритма.
!
Для решения задачи могут быть разработаны алгоритмы, имеющие разную сложность. Лучшим среди них считается алгоритм, имеющий наименьшую сложность.
Эффективность оценивается количеством элементарных операций, которые необходимо выполнить для решения задачи, а также количеством памяти, требующейся для выполнения алгоритма.

Временная сложность
«Найти книгу с секретом»
Сложность алгоритма выражают в виде функции от объёма входных данных.
Задание. Оцените сложность алгоритмов:
«Поиск в телефонной книге»
В сейфе оказался клочок страницы с фамилией и первой цифрой номера телефона. Надо найти страницу с нужной фамилией в телефонном справочнике, в котором 1000 страниц .
Сложность алгоритма будет O(log2n).
Таким образом, в книге объёмом в 1000 страниц страница с нужной фамилией находится не больше, чем за O(log21000) ≈ 10 раз.
В данном случае, за счет сортировки имен по алфавиту, можно сократить поиск, применив метод половинного деления (открыв книгу примерно в середине, мы уменьшаем размер «оставшейся проблемы» вдвое).
При линейном поиске – последовательной проверки всех книг подряд – сложность, в худшем случае, будет равна количеству книг, т.е. O(n) = 1000.
В старинной библиотеке в одном из 1000 томов, посвященных кладам и тайникам, спрятана книга-сейф. Надо найти ее.

X40
Задание. Найти
Пример 4
Алгоритм «Возведение числа в натуральную степень (xn)»
Запишем n в двоичной системе счисления.
Заменим каждую 1 парой букв КХ, а каждый 0 – буквой К.
Вычеркнем крайнюю левую пару КХ.
Полученная строка, читаемая слева направо, даёт правило быстрого вычисления хn, если букву К рассматривать как операцию возведения результата в квадрат, а букву X – как операцию умножения результата на х. Вначале результат равен х.
К
Х
К
К
Х
К
К
К
возведение результата в Квадрат
К
умножение результата на Х
Х
1
0
1
0
0
0
40 = 2
х2
х4
х5
х10
х20
х40

Алгоритм – конечная система правил, сформулированных на языке исполнителя, которая определяет последовательность перехода от допустимых исходных данных к конечному результату и обладает свойствами дискретности, детерминированности, понятности, результативности, конечности и массовости.
Исполнитель алгоритма – субъект или устройство, способные правильно интерпретировать описание алгоритма и выполнить содержащийся в нём перечень действий.
Один и тот же алгоритм может быть записан разными способами: на естественном языке, псевдокодом, с помощью блок-схем, на языке программирования и т. д.
Теория алгоритмов предоставляет аппарат анализа различных алгоритмов решения одной и той же задачи, на основе которого можно выбрать самый эффективный (наилучший) алгоритм.

Алгоритм состоит из команд. Команда – отдельная инструкция в описании алгоритма. Шаг алгоритма – отдельное действие, которое исполнитель выполняет по команде. Вычислительным процессом, порождённым алгоритмом, называется последовательность шагов алгоритма, пройденных при его исполнении.
Сложность алгоритма – количество элементарных шагов (действий) в вычислительном процессе этого алгоритма. Наряду со сложностью важной характеристикой алгоритма является эффективность. Эффективность оценивается количеством элементарных операций, которые необходимо выполнить для решения задачи, а также количеством памяти, требующейся для выполнения алгоритма.

Вопросы и задания
Задание 1. Автомат получает на вход трёхзначное число. По этому числу строится новое число по следующим правилам:
Складываются первая и вторая, а также вторая и третья цифры исходного числа.
Полученные два числа записываются друг за другом в порядке убывания (без разделителей).
Укажите наименьшее число, в результате обработки которого автомат выдаст число 1711.
Решение:
Единственный способ разбить запись 1711 на два числа – это 17 и 11.
Чтобы число было меньше, надо чтобы сумма первой и второй цифр была наименьшей, в данном случае 11.
Сумма значений двух последних цифр равна 17. Не трудно заметить, что 17 = 8 + 9 = 9 + 8. Других вариантов нет.
Тогда 11 = 2 + 9 = 3 + 8. Выбираем пару, которая даст ме́ньшее число.
Ответ: 298.

Вопросы и задания
Задание 2. Подсчитайте сложность алгоритма сложения двух натуральных чисел «столбиком» при условии, что одно из них состоит из n, а второе – из m десятичных цифр.
Решение:
Сложение двух чисел столбиком в случае, если одно из них состоит из n, а другое – из m цифр требует не более max(n, m) сложений и не более max(n, m) запоминаний (в случае перехода через десяток).
Т.е. данный алгоритм имеет сложность порядка O(n+m).
Выражение показывает только порядок величины – постоянные факторы в нем не учитываются.

Вопросы и задания
Задание 3. Есть двое песочных часов: на 3 и на 8 минут. Для приготовления эликсира бессмертия его надо варить ровно 7 минут. Как это сделать? Придумайте систему команд исполнителя Колдун. Запишите с их помощью план действий исполнителя по приготовлению эликсира.
Графический способ решения:

Вопросы и задания
Задание 4. Приведите примеры алгоритмов, с которыми вы встречались на биологии, математике, физике.

Вопросы и задания
Задание 5. Двое мальчиков катались на лодке. К берегу подошли два солдата. Лодка так мала, что на ней могут переправиться двое мальчиков или только один солдат. Как солдатам переправиться через реку?