Содержание
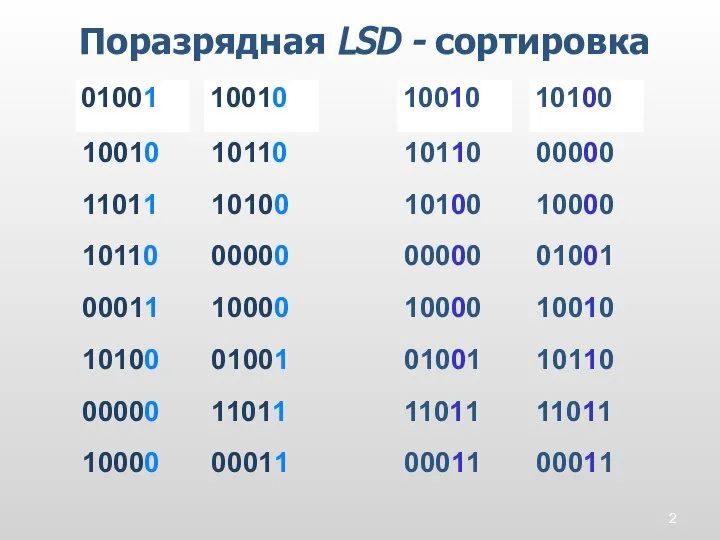
- 2. Поразрядная LSD - сортировка
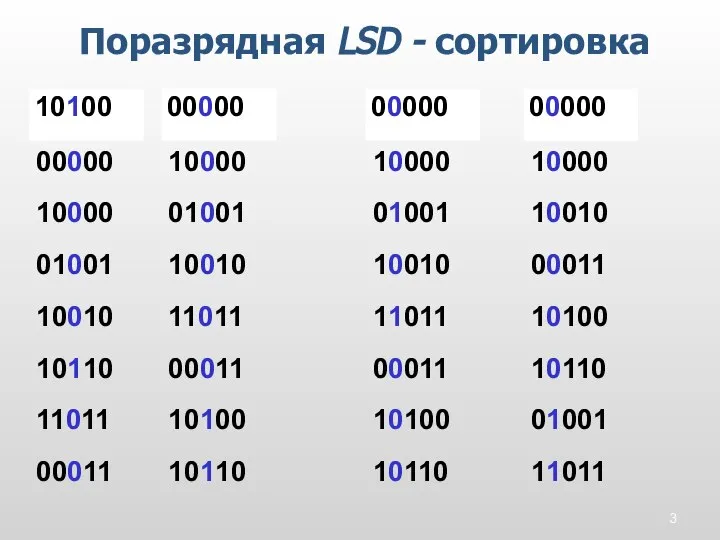
- 3. Поразрядная LSD - сортировка
- 4. Поразрядная LSD - сортировка LSD-сортировка цикл для i от 0 до D нц || D –
- 5. Очереди по приоритетам Во многих приложениях требуется обработка записей с упорядоченными определенным образом ключами: не обязательно
- 6. Структура данных, поддерживающая операции вставки нового элемента; удаления элемента с максимальным значением ключа называется очередью по
- 7. • Системы моделирования – каждое событие системы характеризуется моментом возникновения, это помогает обслуживать события в хронологическом
- 8. На практике очереди по приоритетам более сложны: • создать очередь по приоритетам из N заданных элементов;
- 9. Базовые структуры для очереди: односвязный список, двусвязный список массив. Каждая из описанных процедур может быть реализована
- 10. Процедура вставки Вставлять элемент в начало очереди. Вставлять элемент в конец очереди. Вставлять элемент в заданное
- 11. Упорядоченные последовательности элементов Процедура вставки требует просмотра всей последовательности элементов - O(n). Процедура удаления и поиска
- 12. Неупорядоченные последовательности Процедура вставки выполняется за постоянное время – O(1). Процедура удаления и поиска требует просмотра
- 13. Представление очереди с помощью пирамиды Частично упорядоченный массив; в корне дерева (первый элемент массива) находится элемент
- 14. 2 7 9 4 5 1 8 3 8 9 Представление очереди пирамидой 10 2 7
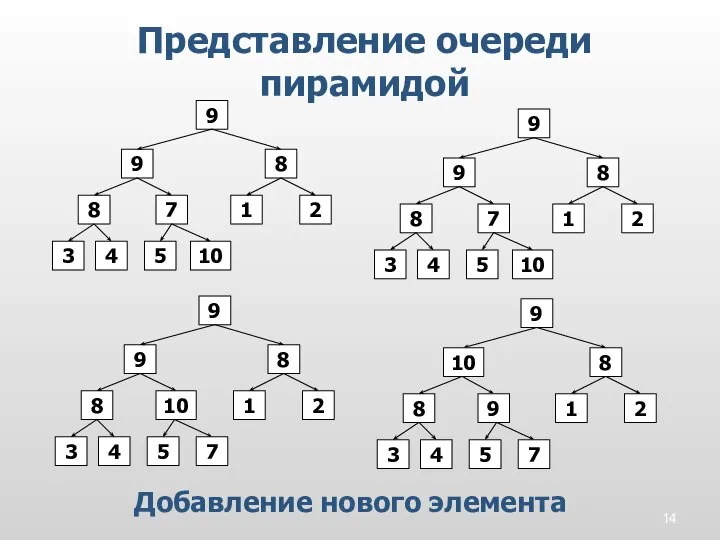
- 15. Представление очереди пирамидой Добавление нового элемента Добавление нового элемента в конец массива. Передвижение элемента к своему
- 16. Представление очереди пирамидой 2 4 5 1 8 3 8 7 9 9 10 Удаление максимального
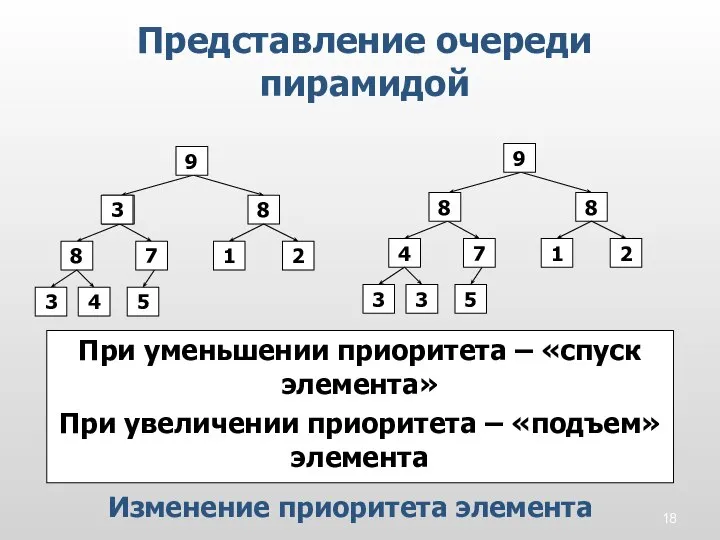
- 17. Представление очереди пирамидой Удаление максимального элемента Обмен нулевого и последнего элемента Удаление последнего элемента массива. Перестройка
- 18. Представление очереди пирамидой Изменение приоритета элемента 2 4 5 1 8 3 8 7 9 9
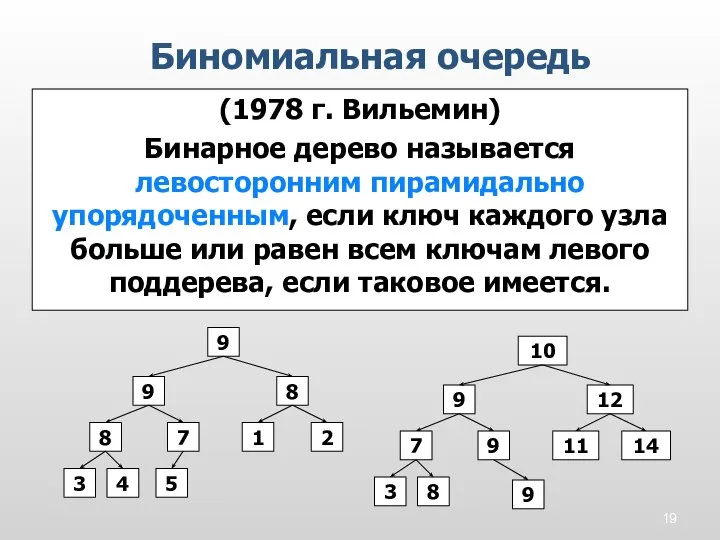
- 19. Биномиальная очередь (1978 г. Вильемин) Бинарное дерево называется левосторонним пирамидально упорядоченным, если ключ каждого узла больше
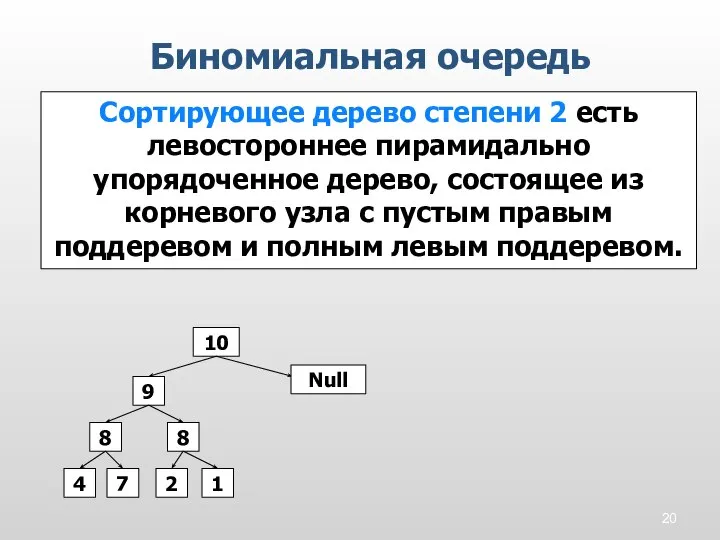
- 20. Биномиальная очередь Сортирующее дерево степени 2 есть левостороннее пирамидально упорядоченное дерево, состоящее из корневого узла с
- 21. Биномиальная очередь Левый потомок сортирующего дерева степени 2 называется биномиальным деревом. • Кол-во узлов сортирующего дерева
- 22. Биномиальная очередь Если реализация биномиального дерева выполнена на основе связных структур, то объединение двух деревьев одинакового
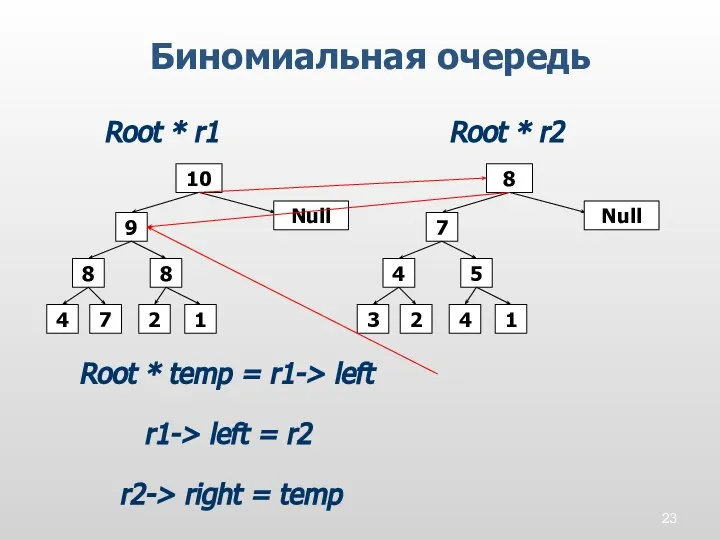
- 23. Биномиальная очередь 8 10 7 2 4 8 9 1 Null 5 8 2 4 3
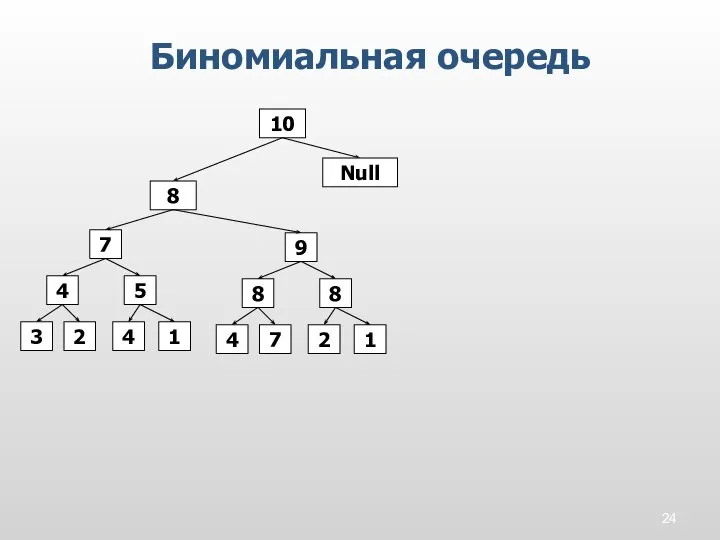
- 24. Биномиальная очередь 8 10 7 2 4 8 9 1 5 8 2 4 3 4
- 25. Биномиальная очередь Биномиальная очередь представляет собой набор сортирующих деревьев степени 2 , ни одно из которых
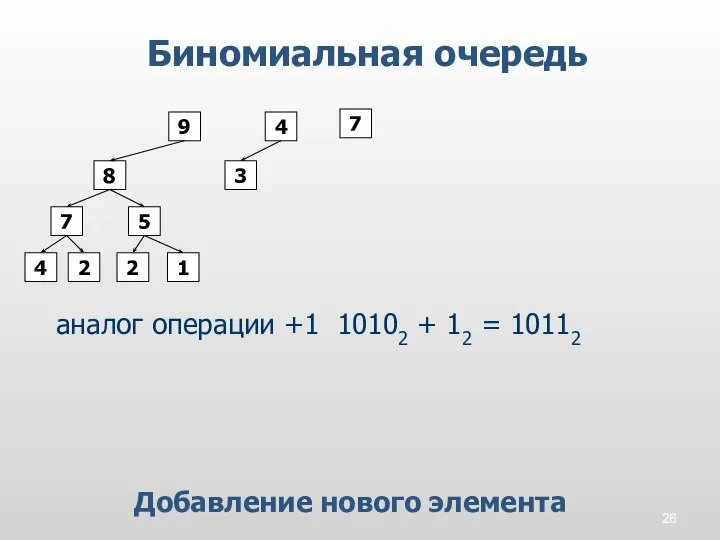
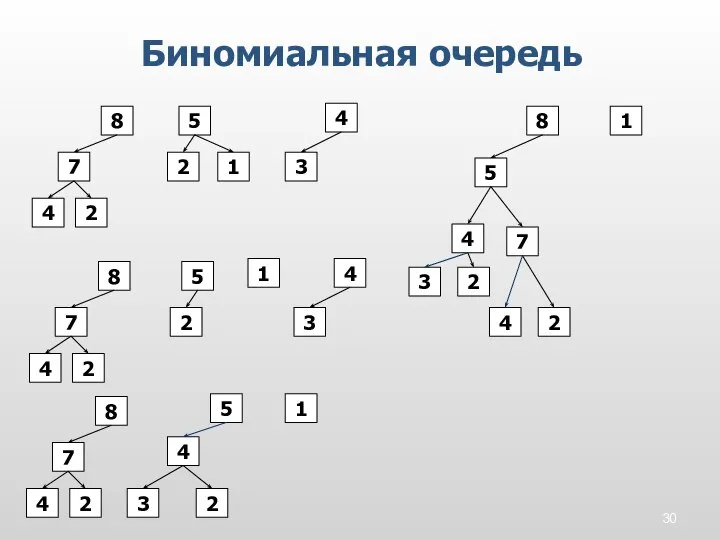
- 26. Биномиальная очередь 3 5 9 2 2 1 4 4 7 8 Добавление нового элемента аналог
- 27. Биномиальная очередь Алгоритм добавления нового элемента проинициализировать новый элемент как 1-дерево переноса i=0 пока не обнаружится
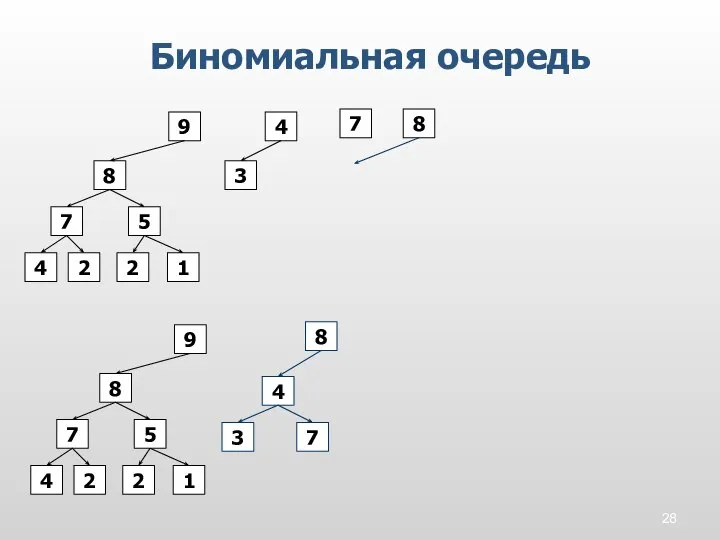
- 28. Биномиальная очередь 3 5 9 2 2 1 4 4 7 8 7 8 5 9
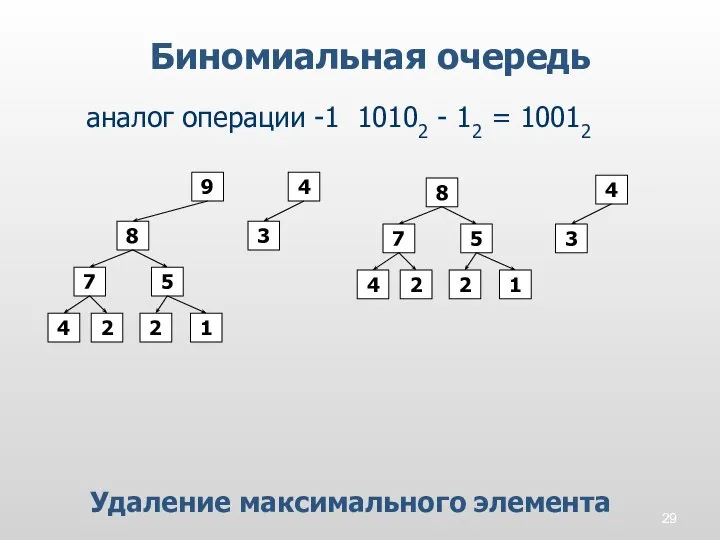
- 29. Биномиальная очередь аналог операции -1 10102 - 12 = 10012 3 5 9 2 2 1
- 30. Биномиальная очередь 5 2 2 1 4 7 8 3 4 2 4 7 8 5
- 31. Биномиальная очередь Алгоритм удаления элемента найти дерево 2i в корне которого расположен максимальный элемент. удалить максимальный
- 32. записать полученное дерево в дерево 2i+1 переноса. i=i+1 кц Биномиальная очередь
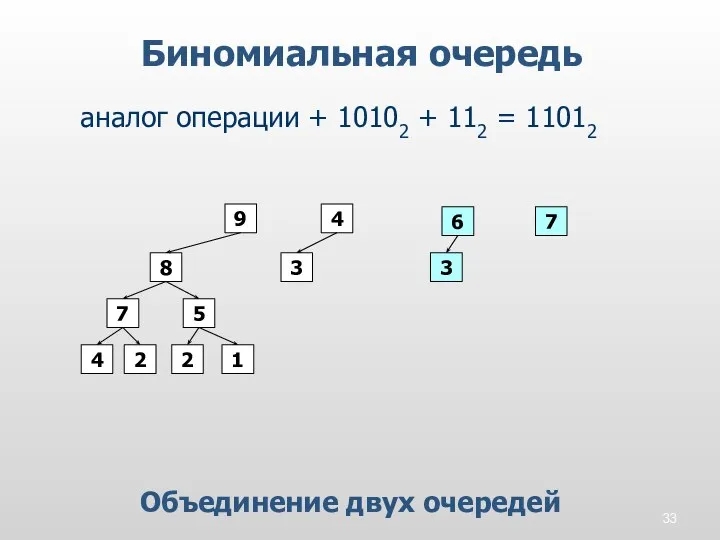
- 33. Биномиальная очередь Объединение двух очередей аналог операции + 10102 + 112 = 11012 3 5 9
- 35. Скачать презентацию


















 Представление информации
Представление информации Алгоритм. Свойства. Способы записи. Линейные алгоритмы
Алгоритм. Свойства. Способы записи. Линейные алгоритмы 5. Python-3 Управляющие конструкции
5. Python-3 Управляющие конструкции Турнир смекалистых
Турнир смекалистых Формирование запроса в поисковой системе
Формирование запроса в поисковой системе АО ТомскНИПИнефть: Работа в специнституте ГИС-автоматизации
АО ТомскНИПИнефть: Работа в специнституте ГИС-автоматизации Введение в Блюпринты. Лекция 1
Введение в Блюпринты. Лекция 1 Вводная презентация в региональный сетевой интернет-проект Дресс-код современного читателя
Вводная презентация в региональный сетевой интернет-проект Дресс-код современного читателя Что такое цикл?
Что такое цикл? Презентация на тему Ребусы по информатике
Презентация на тему Ребусы по информатике  Формулы. Правила ввода формулы
Формулы. Правила ввода формулы Наноксидил. Технический аудит сайта
Наноксидил. Технический аудит сайта Анализ паблика ПостНаука
Анализ паблика ПостНаука Урок информатики, 7 класс
Урок информатики, 7 класс История создания и развития сети интернет
История создания и развития сети интернет Совмещение технологий локального и глобального позиционирования в ОС Android
Совмещение технологий локального и глобального позиционирования в ОС Android Безопасность в интернете. Внеклассное занятие
Безопасность в интернете. Внеклассное занятие Глава 4. Технологии создания и преобразования информационных объектов
Глава 4. Технологии создания и преобразования информационных объектов Компьютер – универсальная машина для работы с информацией
Компьютер – универсальная машина для работы с информацией Яндекс.Медицина
Яндекс.Медицина Worldbox как установить карту By DIMAZOO
Worldbox как установить карту By DIMAZOO Интернет-зависимость и социокультурные предпосылки её возникновения
Интернет-зависимость и социокультурные предпосылки её возникновения Диагностическая работа по информатике в формате ОГЭ
Диагностическая работа по информатике в формате ОГЭ Кодирование информации. Мастер-класс
Кодирование информации. Мастер-класс Эпиграфы
Эпиграфы Инструкция по удаленному подключению к компьютеру ЗКВС
Инструкция по удаленному подключению к компьютеру ЗКВС Графический редактор Paint. Рисуем Велосипед
Графический редактор Paint. Рисуем Велосипед Индивидуальная работа Линейные списки
Индивидуальная работа Линейные списки