Построение новых функций в среде muLisp. Вычисляемые функции

λ -выражение в исчислении Черча
Определение функций и их вычисление в языке LISP основано на λ-исчислении Черча.
λ –выражение является элементом
λ -исчисления и важным механизмом в практическом программировании.
В λ -исчислении Черча функция записывается в следующем виде:
λ (x1,x2,...,xN).fN .
В языке LISP λ -выражение имеет вид:
(LAMBDA (X1 X2 ... XN) FN)

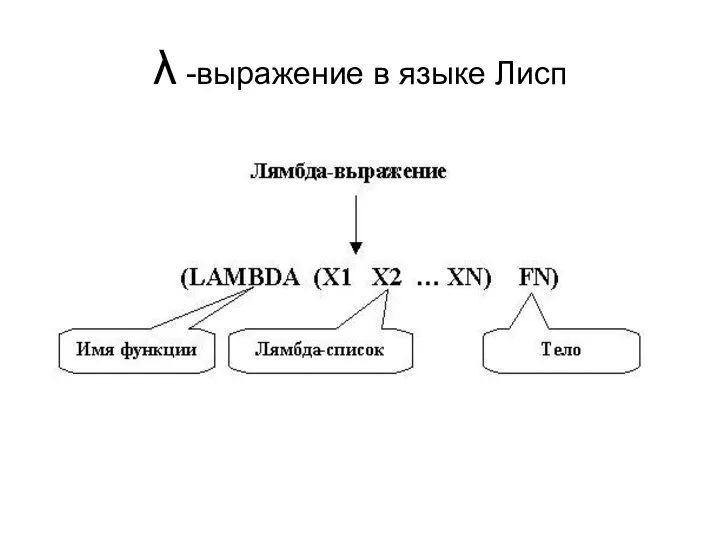
λ -выражение в языке Лисп
В языке LISP λ -выражение имеет вид:
(LAMBDA (X1 X2 ... XN) FN)
Функция LAMBDA предназначена для определения "безымянных" (неименованных) функций и называется вычисляемой функцией (не следует путать с понятием вычислимой функции в теории алгоритмов!).
Первый аргумент вычисляемой функции - (X1 X2 ... XN) является списком (возможно, пустым!). Его называют λ-списком. X1, X2,...,XN называются формальными параметрами.
Второй аргумент функции LAMBDA - FN называется телом. Оно представляет собой произвольное выражение, значение которого может вычислить интерпретатор языка LISP.

λ -выражение в языке Лисп

λ -вызов
Для того, чтобы применить λ -функцию к аргументам, нужно в вызове функции поставить λ -выражение вместо имени функции:
( (LAMBDA (X1 X2 ... XN) FN) A1 A2 ... AN)
Здесь Ai (i=1,2,...,N) - выражения языка LISP, определяющие фактические параметры.
Такую форму вызова называют λ -вызовом.

Вычисление λ -выражения
Вычисление λ -вызова (применение λ -выражения к фактическим параметрам) производится в два этапа. Сначала вычисляются значения фактических параметров и соответствующие формальные параметры связываются с полученными значениями. Этот этап называется связыванием параметров.
На следующем этапе с учетом новых связей вычисляется тело λ -выражения, и полученное значение возвращается в качестве значения
λ -вызова. Формальным параметрам после окончания вычисления возвращаются те связи, которые у них были перед вычислением λ -вызова.
Весь этот процесс называют λ -преобразованием
(λ -конверсией).

Примеры λ -преобразований
$ ((LAMBDA (NUM) (PLUS NUM 1)) 45)
46
$ ((LAMBDA (M N) (COND ((LESSP M N) M) (T N))) 233 123)
233
$ (LAMBDA NIL (PLUS 3 5))
8
$ (LAMBDA () (PLUS 3 5))
8
$ ((LAMBDA (X) (EQ X NIL)) NIL)
T

Особенности использования
λ -преобразований
λ-выражение - это "безымянная" функция, которая пропадает тотчас же после λ -преобразования. Ее трудно использовать снова, так как нельзя вызвать по имени, хотя λ -вызов доступен как списочный объект.
"Безымянные" функции используются, например, при передаче функции в качестве аргумента другой функции или при формировании функции в результате вычислений, другими словами, при синтезе программ.

Пусть требуется описать функцию y=F(x) в зависимости от условия с помощью конструкции LAMBDA :
Пример определения функции с помощью конструкции LAMBDA

((LAMBDA (X)
(COND
( (<= X 2) (* X X))
((AND (> X 2) (< X 6)) (+ X 5))
(T (- X 2)))) 3)
Пример1 определения функции с помощью конструкции LAMBDA

((LAMBDA (X)
(COND
( (<= X 2) (* X X))
((AND (> X 2) (< X 6)) (+ X 5))
(T (- X 2)))) 8)
Пример2 определения функции с помощью конструкции LAMBDA

((LAMBDA (X)
(COND
( (<= X 2) (* X X))
((AND (> X 2) (< X 6)) (+ X 5))
(T (- X 2)))) 0.8)
Пример3 определения функции с помощью конструкции LAMBDA

Примеры λ -преобразований

Построение новых функций в среде muLisp
Именованные функции (функция DEFUN)

Функция DEFUN
Определить новую функцию и дать ей имя можно с помощью функции DEFUN (DEfine FUNction). Функция DEFUN вызывается так:
(DEFUN имя_функции(список_формальных_параметров) тело_функции
)
Тело функции – это последовательность вызовов уже определенных функций.
Функция DEFUN возвращает имя новой функции.
После такого описания к функции можно обращать в данном сеансе работы интерпретатора Лисп.

Формальные параметры функции
Формальные параметры функции называют еще лексическими или статическими переменными.
Связи статической переменной действительны только в пределах той функции, в которой они определены.
Они перестают действовать в функциях, вызываемых во время вычисления, но текстуально описанных вне данной функции.
После вычисления функции, созданные на это время связи формальных параметров ликвидируются и происходит возврат к тому состоянию, которое было до вызова функции.

Пусть требуется описать функцию y=F(x) в зависимости от условия с помощью конструкции DEFUN:
Пример определения функции с помощью конструкции DEFUN

$ (DEFUN F(X)
(COND
( (<= X 2) (* X X))
((and (> X 2) (< X 6)) (+ X 5))
(T (- X 2))))--> F
F
$ (F -3)
9
$ (F 4)
9
$ (F 8)
6
$
Пример определения функции с помощью конструкции DEFUN на языке Лисп

Рекурсивные функции
Рекурсивная функция имеет следующую структуру:
(DEFUN имя_функции(список_формальных_параметров) (COND
(P1 S1)
(P2 S2)
…………….. (Pn Sn)
))
где Pi – предикаты;
Si – выражения произвольной формы.
Причем не менее одно Si должно содержать имя определяемой
функции.

Пример1 рекурсивной функции. Определение факториала.
$ (DEFUN Factorial(N)
(COND
( (ZEROP N) 1)
(T (* N (Factorial (SUB1 N))))
))--> F
FACTORIAL
$ -->
$ F
$ (Factorial 5)
120
$