Содержание
- 2. Что нужно знать: • русский алфавит • принципы работы с числами, записанными в позиционных системах счисления
- 3. Р-06. Вася составляет 5-буквенные слова, в которых есть только буквы С, Л, О, Н, причём буква
- 4. Р-05. Сколько существует различных символьных последовательностей длины 5 в четырёхбуквенном алфавите {A, C, G, T}, которые
- 5. 4) теперь рассматриваем шаблоны, где первая по счёту буква А стоит на второй позиции, их всего
- 6. Р-04. Сколько слов длины 5, начинающихся с гласной буквы, можно составить из букв Е, Г, Э?
- 7. Р-03. Все 4-буквенные слова, составленные из букв К, Л, Р, Т, записаны в алфавитном порядке и
- 8. Решение: 1) самый простой вариант решения этой задачи – использование систем счисления; действительно, здесь расстановка слов
- 9. Р-02. Все 5-буквенные слова, составленные из букв А, О, У, записаны в алфавитном порядке. Вот начало
- 10. Решение (троичная система, идея М. Густокашина): по условию задачи важно только то, что используется набор из
- 11. это напоминает (в самом деле, так оно и есть!) числа, записанные в троичной системе счисления в
- 12. Р-01. Все 5-буквенные слова, составленные из 5 букв А, К, Л, О, Ш, записаны в алфавитном
- 13. Решение: 1) по аналогии с предыдущим решением будем использовать пятеричную систему счисления с заменой А →
- 14. Р-00. Все 5-буквенные слова, составленные из букв А, О, У, записаны в обратном алфавитном порядке. Вот
- 15. Решение: по условию задачи важно только то, что используется набор из трех разных символов, для которых
- 17. Скачать презентацию














 Файл и файловая система
Файл и файловая система Правила оформления информационных источников в работе. 10 класс
Правила оформления информационных источников в работе. 10 класс “Жёлтый блокнот”. Принцип Дирихле
“Жёлтый блокнот”. Принцип Дирихле Моделирование
Моделирование Своя игра. Логика
Своя игра. Логика Разработка и исследование АСУ цеха регенерации ДЭГа
Разработка и исследование АСУ цеха регенерации ДЭГа Цифровая трансформация общества
Цифровая трансформация общества Влияние компьютерных игр на поведение и успеваемость подростков
Влияние компьютерных игр на поведение и успеваемость подростков По инновационному продукту АТС1 и АТС 2 из сферы применения FinTech
По инновационному продукту АТС1 и АТС 2 из сферы применения FinTech Общие теоретические вопросы. Оптимизация – общая постановка задачи. Целевая функция, система ограничений
Общие теоретические вопросы. Оптимизация – общая постановка задачи. Целевая функция, система ограничений Высказывания. Законы логики
Высказывания. Законы логики Система регистрации и аутентификации игрового сервиса
Система регистрации и аутентификации игрового сервиса Кодирование и обработка звуковой информации
Кодирование и обработка звуковой информации NET Framework – программная платформа
NET Framework – программная платформа Интерьер. Дизайнеры
Интерьер. Дизайнеры Компьютерная графика
Компьютерная графика Компьютерные сети. Виды, структура, принципы функционирования
Компьютерные сети. Виды, структура, принципы функционирования Проектирование внутримашинного информационного обеспечения ИС
Проектирование внутримашинного информационного обеспечения ИС Tehniskās dokumentācijas apzīmējumi un terminoloģija
Tehniskās dokumentācijas apzīmējumi un terminoloģija Генератор случайных чисел, константы, работа со строками
Генератор случайных чисел, константы, работа со строками Что такое информация
Что такое информация 9_1dz (1)
9_1dz (1) Винни-Пух и пчелы
Винни-Пух и пчелы Презентация на тему История развития вычислительной техники
Презентация на тему История развития вычислительной техники  Обработка графической информации. Контрольная работа. 7 класс
Обработка графической информации. Контрольная работа. 7 класс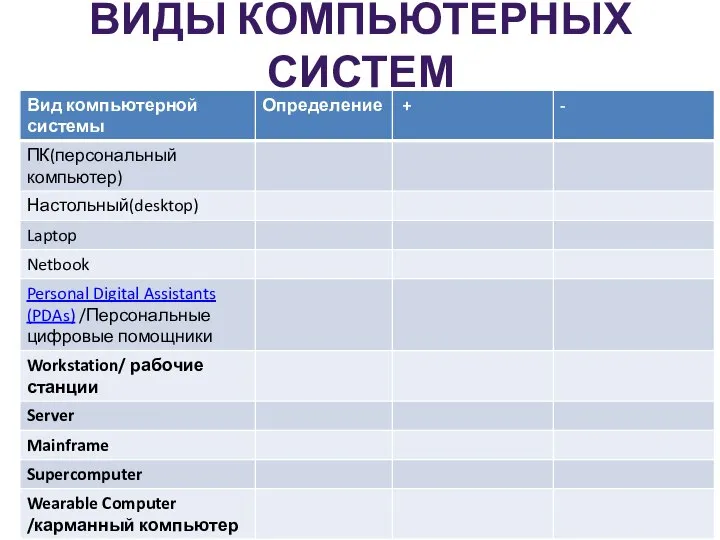 Виды компьютерных систем
Виды компьютерных систем Веселый фермер
Веселый фермер PHP. Разработка блога. Часть 2. Урок 8
PHP. Разработка блога. Часть 2. Урок 8