Содержание
- 2. АЛГОРИТМ ПОСТРОЕНИЯ СБАЛАНСИРОВАННОГО ДЕРЕВА ПОИСКА При добавлении узла считаем баланс его «отца» (p) и «деда» (gp)
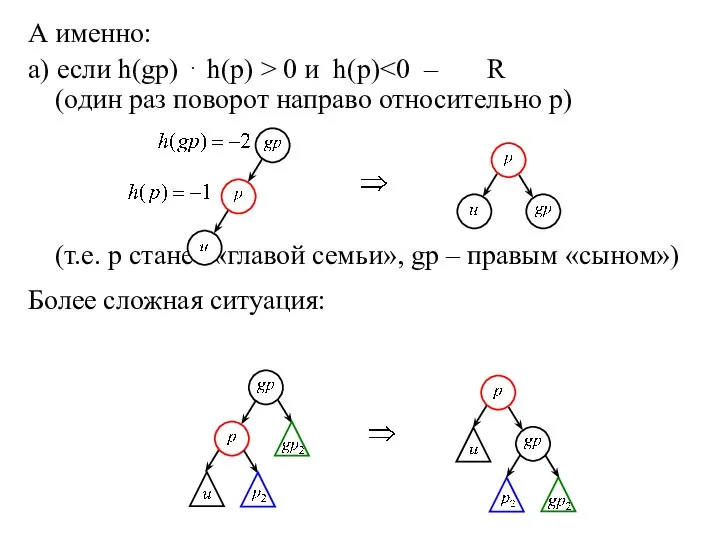
- 3. А именно: а) если h(gp) ⋅ h(p) > 0 и h(p) (один раз поворот направо относительно
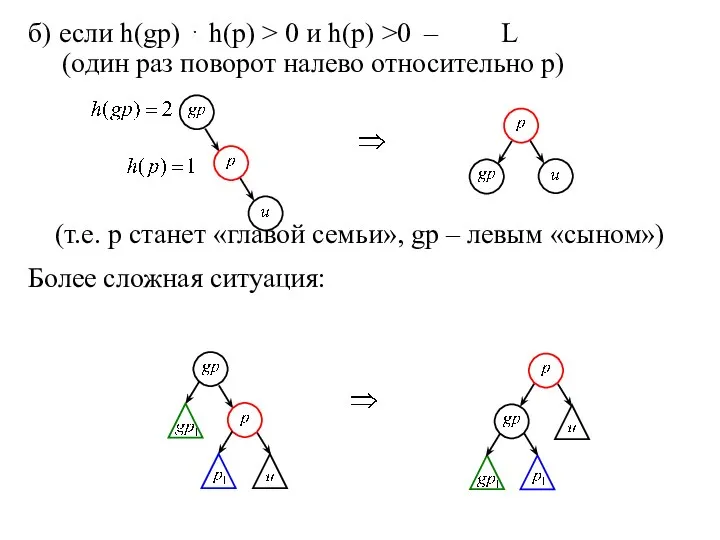
- 4. б) если h(gp) ⋅ h(p) > 0 и h(p) >0 – L (один раз поворот налево
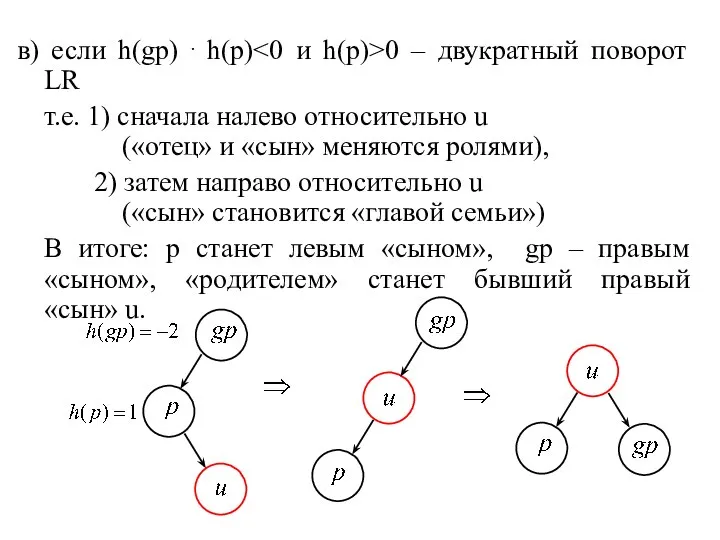
- 5. в) если h(gp) ⋅ h(p) 0 – двукратный поворот LR т.е. 1) сначала налево относительно u
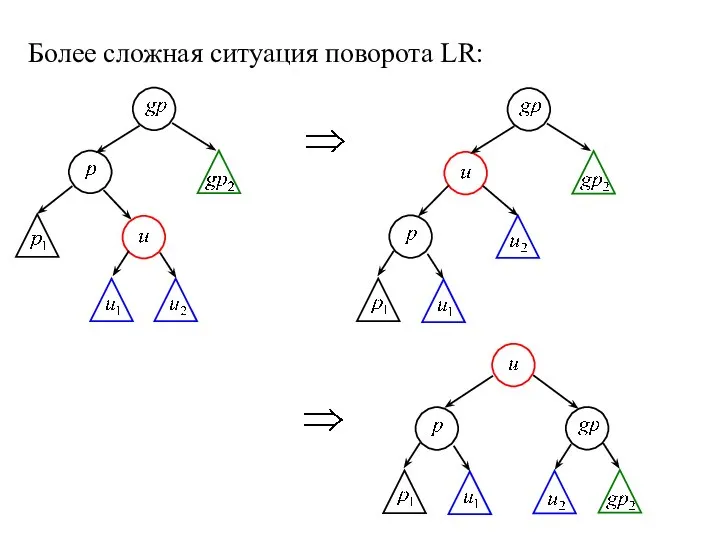
- 6. Более сложная ситуация поворота LR:
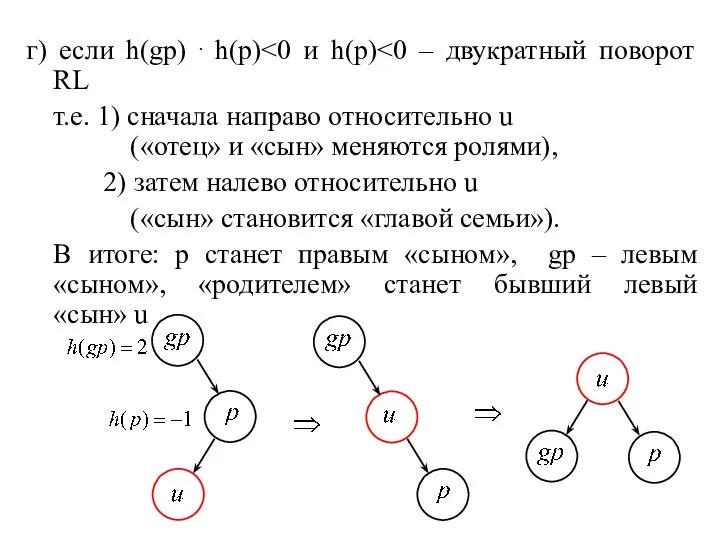
- 7. г) если h(gp) ⋅ h(p) т.е. 1) сначала направо относительно u («отец» и «сын» меняются ролями),
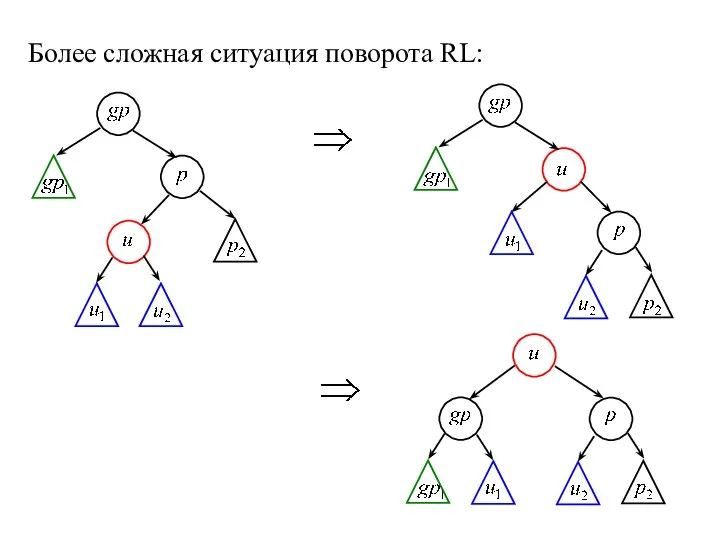
- 8. Более сложная ситуация поворота RL:
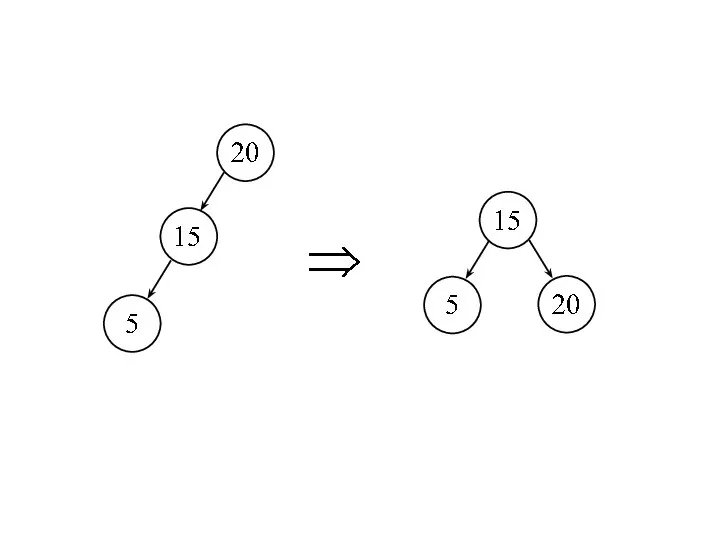
- 9. Задача. Построить сбалансированное дерево для массива ключей {20, 15, 5, 30, 55, 25, 10, 6, 2,
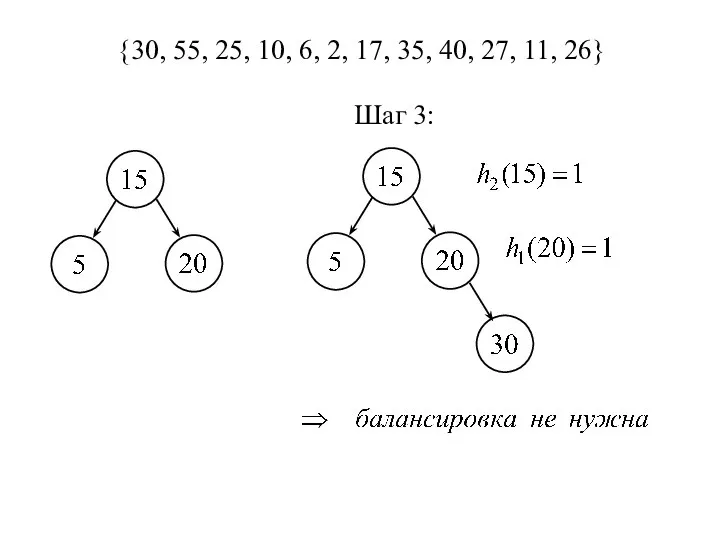
- 11. {30, 55, 25, 10, 6, 2, 17, 35, 40, 27, 11, 26} Шаг 3:
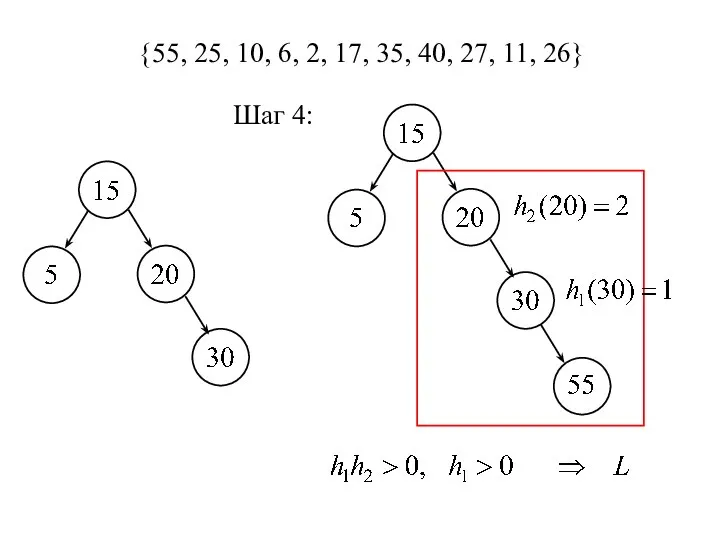
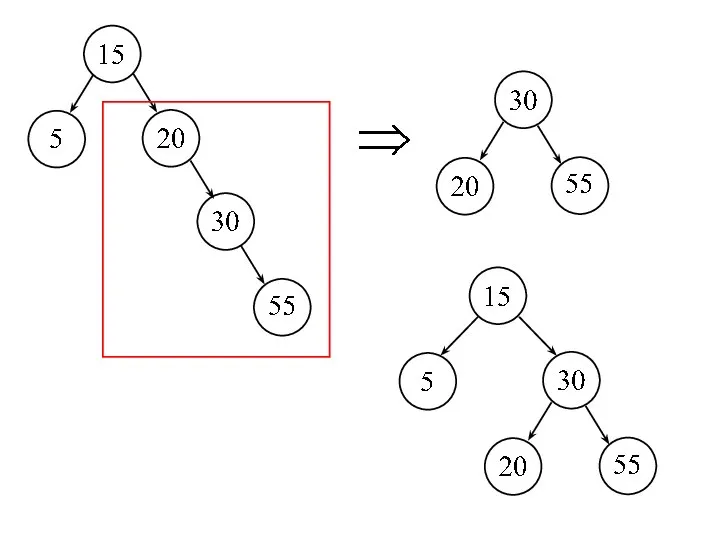
- 12. {55, 25, 10, 6, 2, 17, 35, 40, 27, 11, 26} Шаг 4:
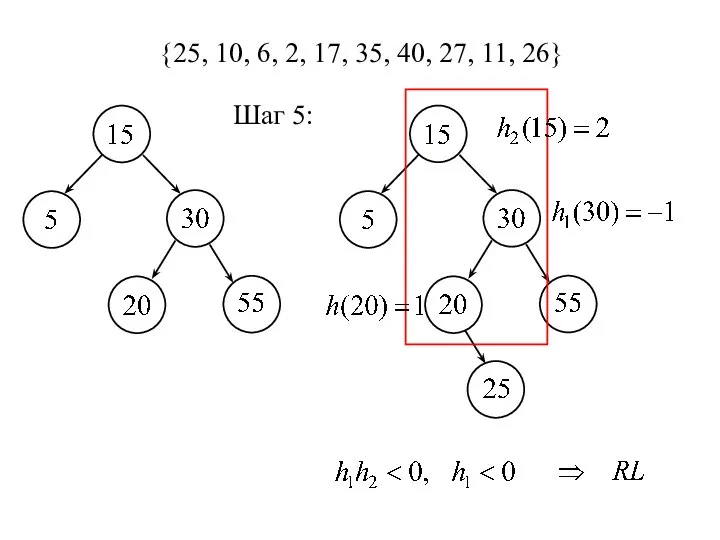
- 14. {25, 10, 6, 2, 17, 35, 40, 27, 11, 26} Шаг 5:
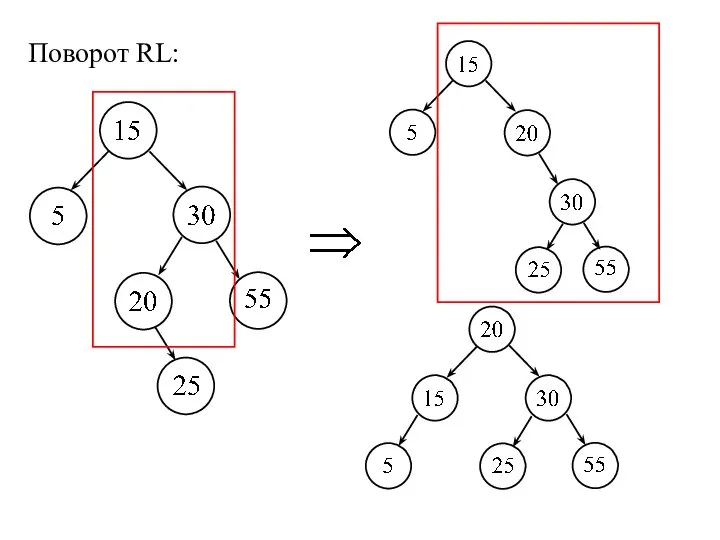
- 15. Поворот RL:
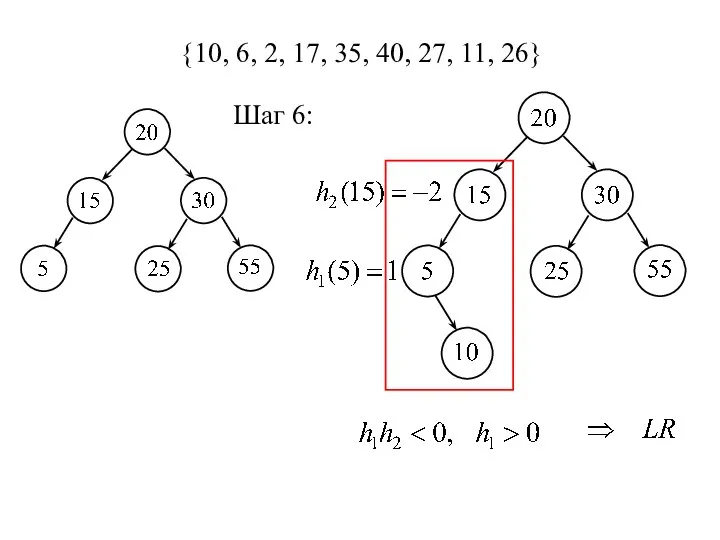
- 16. {10, 6, 2, 17, 35, 40, 27, 11, 26} Шаг 6:
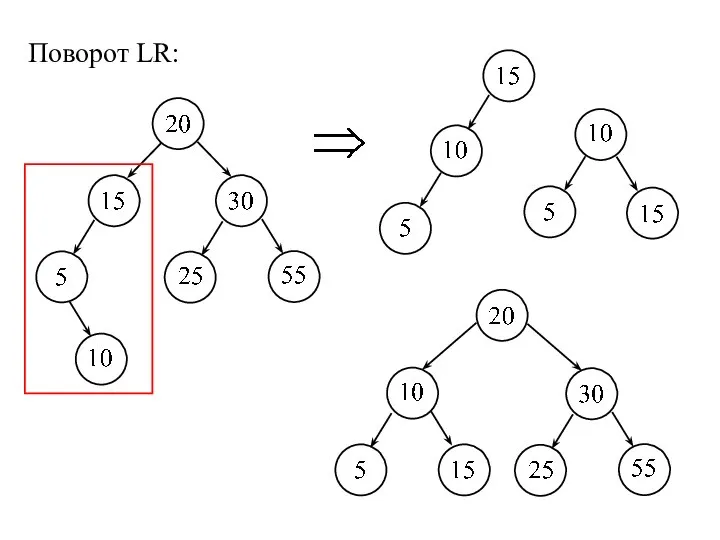
- 17. Поворот LR:
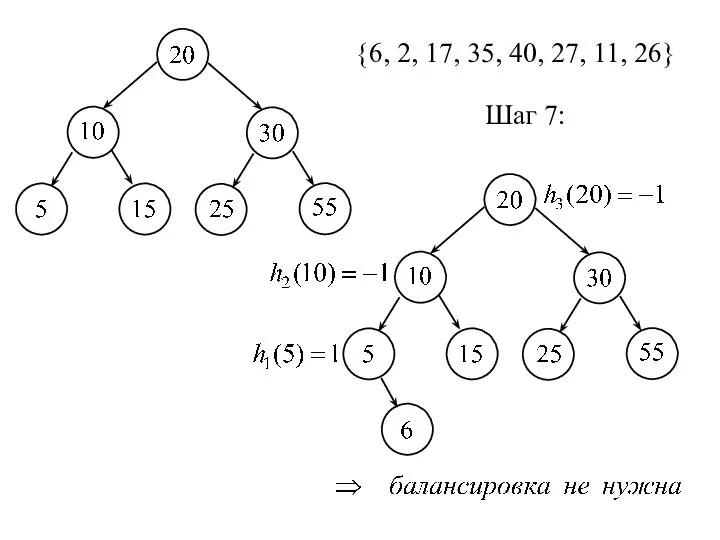
- 18. {6, 2, 17, 35, 40, 27, 11, 26} Шаг 7:
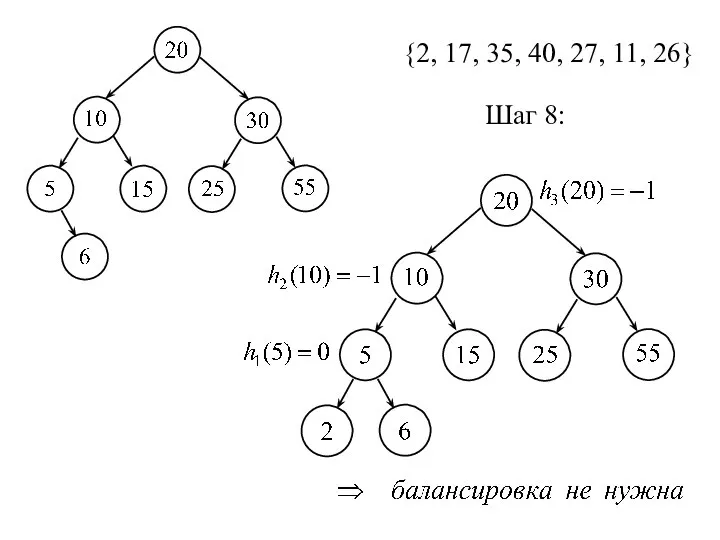
- 19. {2, 17, 35, 40, 27, 11, 26} Шаг 8:
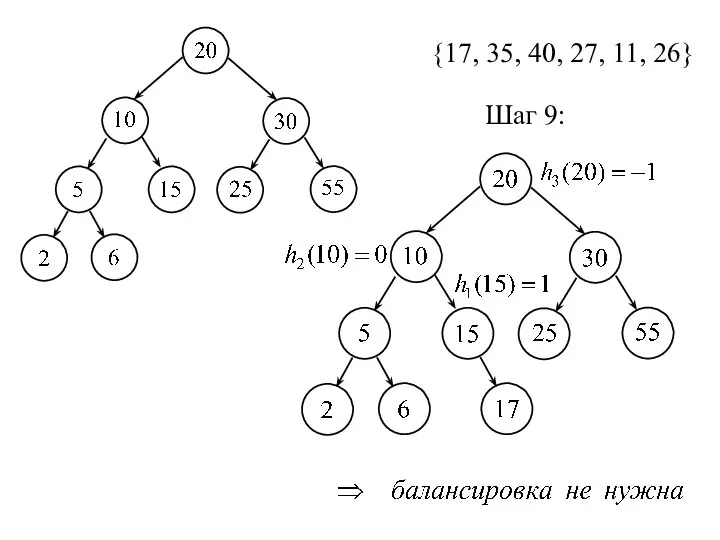
- 20. {17, 35, 40, 27, 11, 26} Шаг 9:
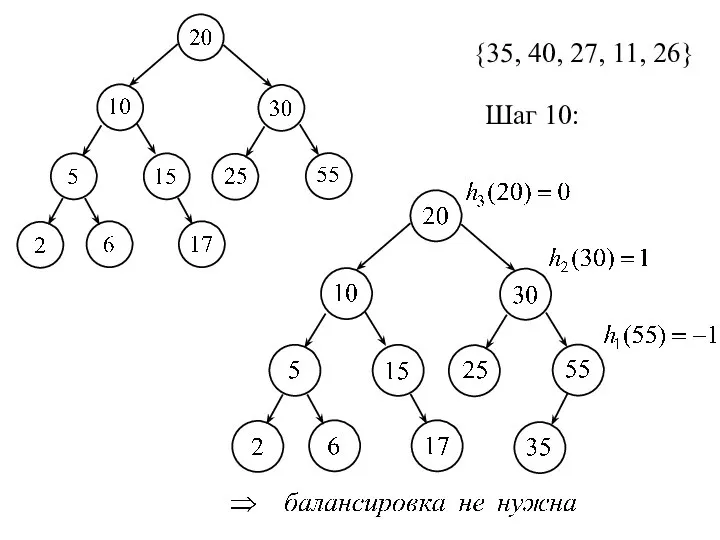
- 21. {35, 40, 27, 11, 26} Шаг 10:
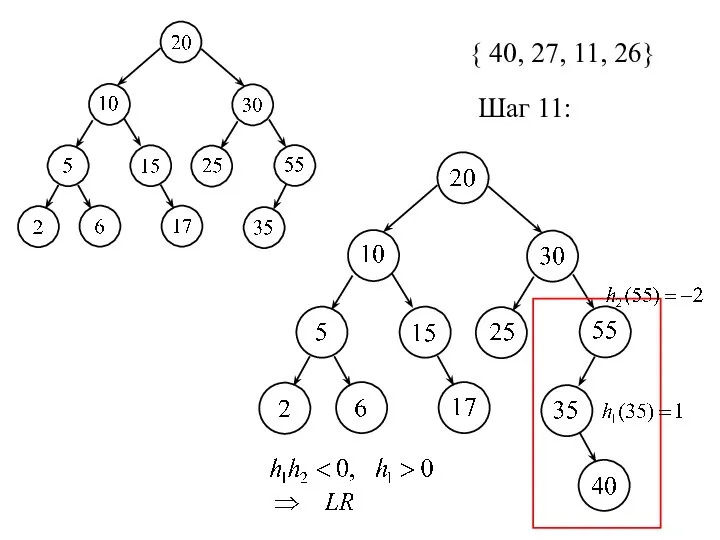
- 22. { 40, 27, 11, 26} Шаг 11:
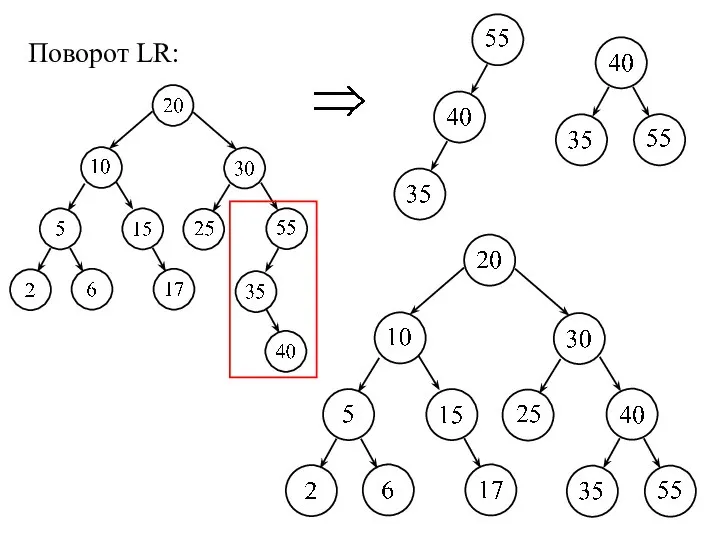
- 23. Поворот LR:
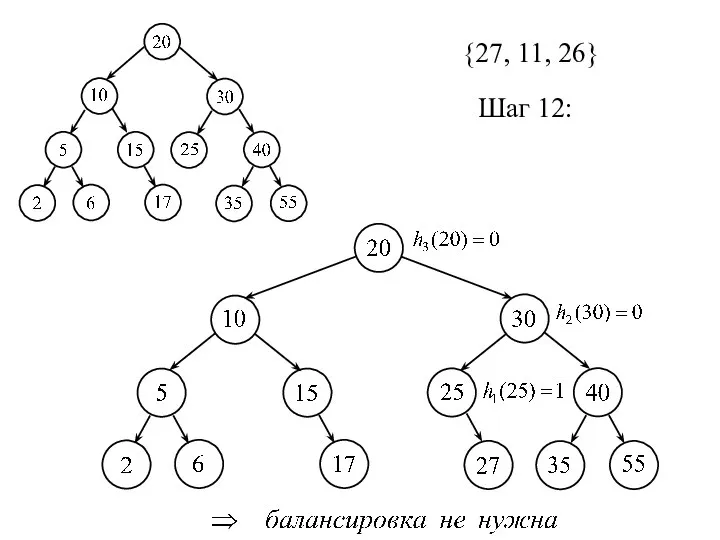
- 24. {27, 11, 26} Шаг 12:
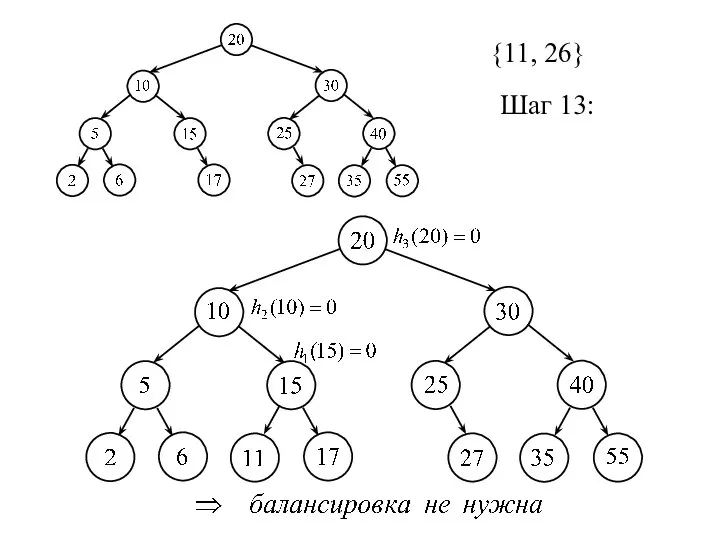
- 25. {11, 26} Шаг 13:
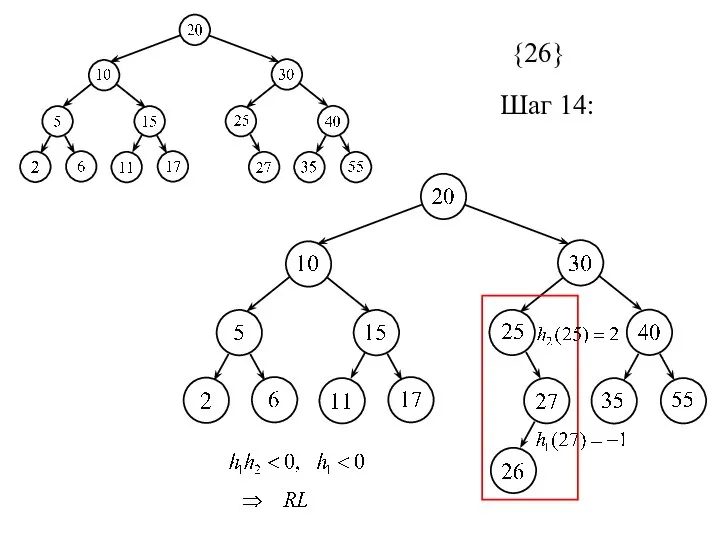
- 26. {26} Шаг 14:
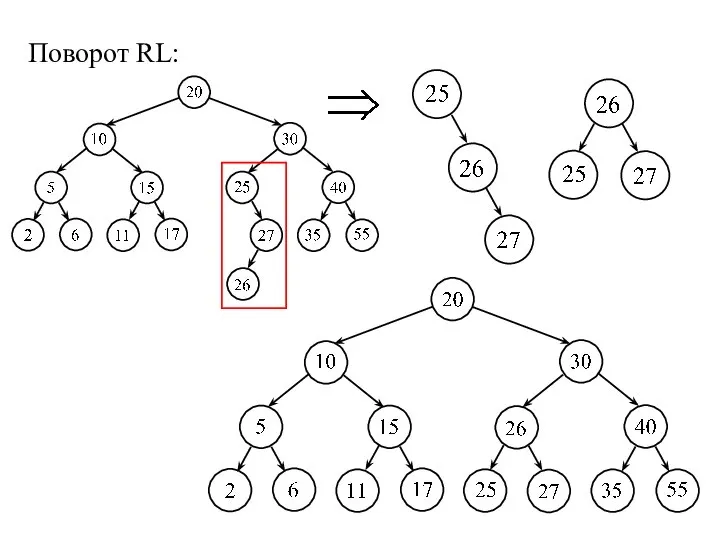
- 27. Поворот RL:
- 29. Скачать презентацию


 358278
358278 Проект Фабрика согласия (пропаганда и цензура)
Проект Фабрика согласия (пропаганда и цензура) Диагностика и ремонт печатающей техники
Диагностика и ремонт печатающей техники Themify Yuntsevich
Themify Yuntsevich Правила поведения в чатах
Правила поведения в чатах Шаблон для заказной разработки
Шаблон для заказной разработки Установка Ubuntu
Установка Ubuntu База данных (БД). Лабораторная работа 2
База данных (БД). Лабораторная работа 2 Mersekler
Mersekler Циклический код Хэмминга
Циклический код Хэмминга MSK-IX 25 лет
MSK-IX 25 лет Поисковые системы Республики Конго
Поисковые системы Республики Конго Виды в трехмерном пространстве. Создание 3D объектов в CAD-системах
Виды в трехмерном пространстве. Создание 3D объектов в CAD-системах Информационно-сыскной отдел “Охотники за фейками”
Информационно-сыскной отдел “Охотники за фейками” Nfilm.net. О сайте
Nfilm.net. О сайте Периодизация и программирование в подготовительном периоде
Периодизация и программирование в подготовительном периоде Подходы к систематическому наблюдению активности региональной элиты
Подходы к систематическому наблюдению активности региональной элиты Примеры использования внешних устройств. Программное обеспечение внешних устройств
Примеры использования внешних устройств. Программное обеспечение внешних устройств Технология создания виртуальной выставки
Технология создания виртуальной выставки Программный комплекс AutoCad
Программный комплекс AutoCad Медиа-карта региона: культура
Медиа-карта региона: культура Теги и атрибуты HTML
Теги и атрибуты HTML Формы представления информации
Формы представления информации Презентация на тему Урок Photoshop
Презентация на тему Урок Photoshop  Двоичное кодирование
Двоичное кодирование Создание и редактирование презентаций
Создание и редактирование презентаций Разработка сайта История создания и развития HTML
Разработка сайта История создания и развития HTML История создания Интернета
История создания Интернета