Построение таблиц истинности

Построение таблиц истинности.
Рассмотрим пример №1, где значение сложного высказывания можно определить с помощью построения таблицы истинности.

Пример №1.
В классе оказалось разбито стекло. Учитель объясняет директору:
Это сделал Коля или Саша. Но Саша этого не делал, так как в это время сдавал мне зачет. Следовательно, это сделал Коля. Прав ли учитель?

Решение:
Сначала выделим составляющие простые высказывания и определим их количество;
К = Это сделал Коля.
С = Это сделал Саша.
Определим форму высказывания:
Е=(К + С) & С К

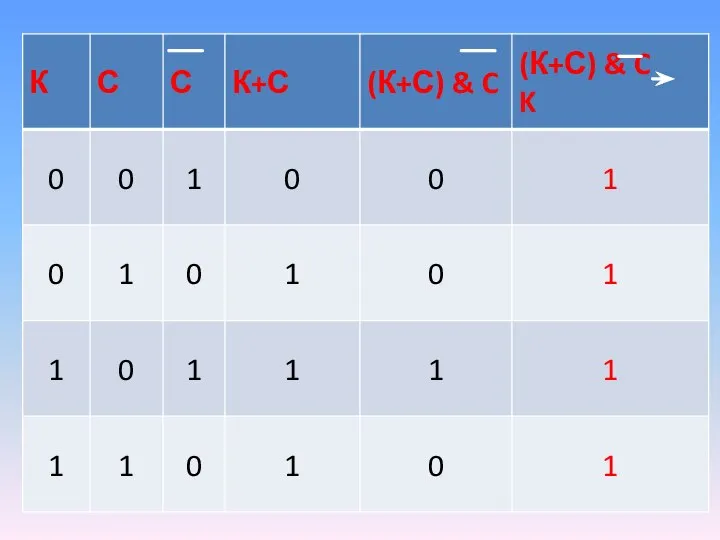
Построим таблицу истинности:
Для этого определим количество строк и количество столбцов в таблице. Так как каждое из простых высказываний может принимать всего два значения(0 и 1), то количество разных комбинаций значений n высказываний – 2^n.
Колличество строк = 2^n (2^2+1=5)
Колличество столбцов = количество простых высказываний + количество логических операций (2+4=6)

Вывод:
Мы получили в последнем столбце все единицы. Это значит, что значение истинно при любых значениях простых высказываний К и С. Следовательно учитель
прав.