Содержание
- 2. Элементы алгебры логики. Логические операции Правила построения таблиц истинности для выражений. Свойства логических операций. 1 2
- 3. Алгебра логики Логические операции Дизъюнкция Инверсия Конъюнкция
- 4. Основные логические операции
- 5. Логические операции A B A & B 0 0 0 0 0 0 0 1 1
- 6. Логические операции A B A V B 0 0 0 0 0 1 1 1 1
- 7. Логические операции А = 0 инверсия А = 1 инверсия
- 8. Логические выражения Логические выражения могут состоять из более чем двух логических операций. А V B &
- 9. План построения таблицы истинности Посчитать n – число переменных в выражении. (А V B) & C
- 10. План построения таблицы истинности Посчитать n – число переменных в выражении. Подсчитать общее число логических операций
- 11. План построения таблицы истинности Посчитать n – число переменных в выражении. Подсчитать общее число логических операций
- 12. План построения таблицы истинности Посчитать n – число переменных в выражении. Подсчитать общее число логических операций
- 13. План построения таблицы истинности Посчитать n – число переменных в выражении. Подсчитать общее число логических операций
- 14. План построения таблицы истинности Посчитать n – число переменных в выражении. Подсчитать общее число логических операций
- 15. План построения таблицы истинности Посчитать n – число переменных в выражении. Подсчитать общее число логических операций
- 16. План построения таблицы истинности Посчитать n – число переменных в выражении. Подсчитать общее число логических операций
- 17. План построения таблицы истинности Посчитать n – число переменных в выражении. Подсчитать общее число логических операций
- 18. План построения таблицы истинности Посчитать n – число переменных в выражении. Подсчитать общее число логических операций
- 19. План построения таблицы истинности Посчитать n – число переменных в выражении. Подсчитать общее число логических операций
- 20. Построения таблицы истинности Построить таблицу истинности для логического выражения (A & B) & A V B.
- 21. n = 2. Построения таблицы истинности Построить таблицу истинности для логического выражения (A & B) &
- 22. n = 2. Построения таблицы истинности Построить таблицу истинности для логического выражения (A & B) &
- 23. n = 2. Построения таблицы истинности Построить таблицу истинности для логического выражения (A & B) &
- 24. n = 2. Построения таблицы истинности Построить таблицу истинности для логического выражения (A & B) &
- 25. n = 2. Построения таблицы истинности Построить таблицу истинности для логического выражения (A & B) &
- 26. n = 2. Построения таблицы истинности Построить таблицу истинности для логического выражения (A & B) &
- 27. n = 2. Построения таблицы истинности Построить таблицу истинности для логического выражения (A & B) &
- 28. n = 2. Построения таблицы истинности Построить таблицу истинности для логического выражения (A & B) &
- 29. n = 2. Построения таблицы истинности Построить таблицу истинности для логического выражения (A & B) &
- 30. n = 2. Построения таблицы истинности Построить таблицу истинности для логического выражения (A & B) &
- 31. n = 2. Построения таблицы истинности Построить таблицу истинности для логического выражения (A & B) &
- 32. n = 2. Построения таблицы истинности Построить таблицу истинности для логического выражения (A & B) &
- 33. n = 2. Построения таблицы истинности Построить таблицу истинности для логического выражения (A & B) &
- 34. n = 2. Построения таблицы истинности Построить таблицу истинности для логического выражения (A & B) &
- 35. n = 2. Построения таблицы истинности Построить таблицу истинности для логического выражения (A & B) &
- 36. n = 2. Построения таблицы истинности Построить таблицу истинности для логического выражения (A & B) &
- 37. n = 2. Построения таблицы истинности Построить таблицу истинности для логического выражения (A & B) &
- 38. n = 2. Построения таблицы истинности Построить таблицу истинности для логического выражения (A & B) &
- 39. n = 2. Построения таблицы истинности Построить таблицу истинности для логического выражения (A & B) &
- 40. n = 2. Построения таблицы истинности Построить таблицу истинности для логического выражения (A & B) &
- 41. n = 2. Построения таблицы истинности Построить таблицу истинности для логического выражения (A & B) &
- 42. n = 2. Построения таблицы истинности Построить таблицу истинности для логического выражения (A & B) &
- 43. Основные свойства логических операций Законы алгебры логики 1. Переместительный (коммутативный) закон. При перестановке местами переменных в
- 44. Основные свойства логических операций Законы алгебры логики 2. Сочетательный (ассоциативный) закон. При одинаковых знаках операций скобки
- 45. Основные свойства логических операций Законы алгебры логики 3. Распределительный (дистрибутивный) закон. A & (B V C)
- 46. Основные свойства логических операций Законы алгебры логики 4. Закон двойного отрицания. A = A – (–
- 47. Основные свойства логических операций Законы алгебры логики 5. Закон исключённого третьего. A & A = 0
- 48. Основные свойства логических операций Законы алгебры логики 6. Закон повторения. A & A = А Конъюнкция
- 49. Основные свойства логических операций Законы алгебры логики 6. Закон повторения. A & A = А Конъюнкция
- 50. Основные свойства логических операций Законы алгебры логики 7. Законы операций с 0 и 1. A &
- 51. Основные свойства логических операций Законы алгебры логики 8. Законы общей инверсии. A & B = А
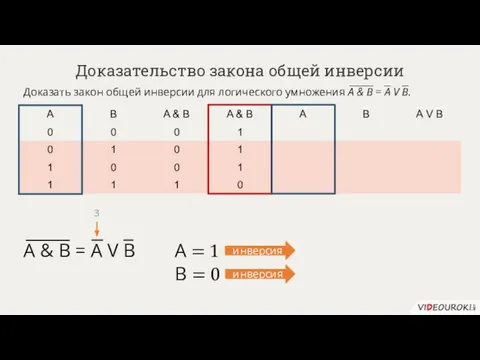
- 52. Доказательство закона общей инверсии Доказать закон общей инверсии для логического умножения n = 2. A &
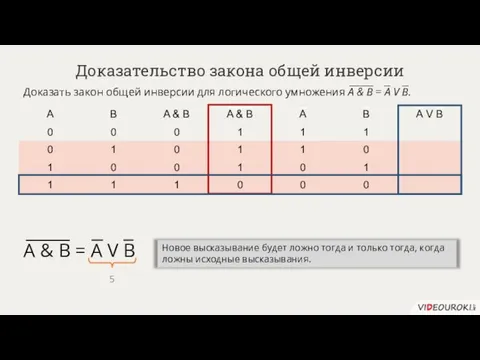
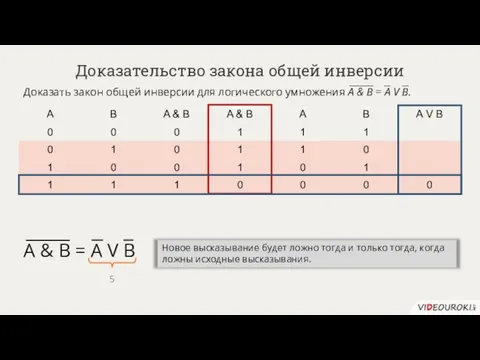
- 53. Доказательство закона общей инверсии Доказать закон общей инверсии для логического умножения A & B = А
- 54. Доказательство закона общей инверсии Доказать закон общей инверсии для логического умножения A & B = А
- 55. Доказательство закона общей инверсии Доказать закон общей инверсии для логического умножения A & B = А
- 56. Доказательство закона общей инверсии Доказать закон общей инверсии для логического умножения A & B = А
- 57. Доказательство закона общей инверсии Доказать закон общей инверсии для логического умножения A & B = А
- 58. Доказательство закона общей инверсии Доказать закон общей инверсии для логического умножения A & B = А
- 59. Доказательство закона общей инверсии Доказать закон общей инверсии для логического умножения A & B = А
- 60. Доказательство закона общей инверсии Доказать закон общей инверсии для логического умножения A & B = А
- 61. Доказательство закона общей инверсии Доказать закон общей инверсии для логического умножения A & B = А
- 62. Доказательство закона общей инверсии Доказать закон общей инверсии для логического умножения A & B = А
- 63. Доказательство закона общей инверсии Доказать закон общей инверсии для логического умножения A & B = А
- 64. Доказательство закона общей инверсии Доказать закон общей инверсии для логического умножения A & B = А
- 65. Доказательство закона общей инверсии Доказать закон общей инверсии для логического умножения A & B = А
- 66. Доказательство закона общей инверсии Доказать закон общей инверсии для логического умножения A & B = А
- 67. Доказательство закона общей инверсии Доказать закон общей инверсии для логического умножения A & B = А
- 68. Пример Найти значение логического выражения (D > 1) V (D D = 1. Решение: (1 >
- 69. Построение таблиц истинности для логических выражений. Свойства логических операций
- 71. Скачать презентацию

































































 Выбор провайдера и виртуальная организация взаимодействия с ним
Выбор провайдера и виртуальная организация взаимодействия с ним 1C:Зарплата и управление персоналом. Отражение изменений законодательства, связанных с коронавирусом
1C:Зарплата и управление персоналом. Отражение изменений законодательства, связанных с коронавирусом Комп'ютерні віруси
Комп'ютерні віруси Гиперссылки. Урок 5
Гиперссылки. Урок 5 Язык Информатики
Язык Информатики Adseed is a multi-platform advertising network
Adseed is a multi-platform advertising network Монтаж проекта
Монтаж проекта Укрощение строптивых. Оптимизация и реструктура проекта для увеличения доступности CodeEvening
Укрощение строптивых. Оптимизация и реструктура проекта для увеличения доступности CodeEvening Створення таблиці
Створення таблиці Транспортный уровень (Transport)
Транспортный уровень (Transport) programmirovanie_l2-2016
programmirovanie_l2-2016 Исследование и реализация хеш-функции SHA-2
Исследование и реализация хеш-функции SHA-2 Внешние устройства компьютера
Внешние устройства компьютера Двумерные массивы. 9 класс
Двумерные массивы. 9 класс Тест Сети
Тест Сети Безопасный интернет. 4 класс
Безопасный интернет. 4 класс Векторная графика и векторные редакторы
Векторная графика и векторные редакторы Язык запросов SQL
Язык запросов SQL Программное обеспечение ЭВМ
Программное обеспечение ЭВМ Применение и наладка протоколов маршрутизации TCP, UDP, SCTP
Применение и наладка протоколов маршрутизации TCP, UDP, SCTP Редактирование текста
Редактирование текста Организация сетевой безопасности организации на основе настройки межсетевого экрана
Организация сетевой безопасности организации на основе настройки межсетевого экрана Урок 8 Создание графических изображений
Урок 8 Создание графических изображений Бинарные деревья
Бинарные деревья Искусственный интеллект при подборе персонала
Искусственный интеллект при подборе персонала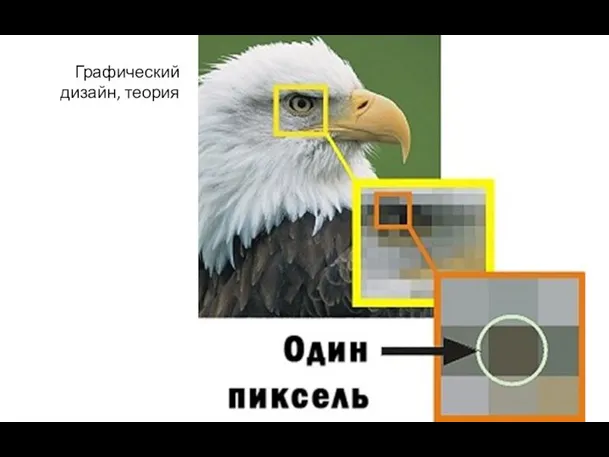 2.3 Введение, пиксели
2.3 Введение, пиксели 4ed6a18c974140b9baffd227bfab0cb7 (1)
4ed6a18c974140b9baffd227bfab0cb7 (1) Windows 2000
Windows 2000