Содержание
- 2. 1. ПРЕДСТАВЛЕНИЕ ЧИСЛОВОЙ ИНФОРМАЦИИ В ЦИФРОВЫХ АВТОМАТАХ Информация в памяти ЭВМ записывается в форме цифрового двоичного
- 4. Ячейки памяти и регистры состоят из элементов памяти. Каждый из таких электрических элементов может находиться в
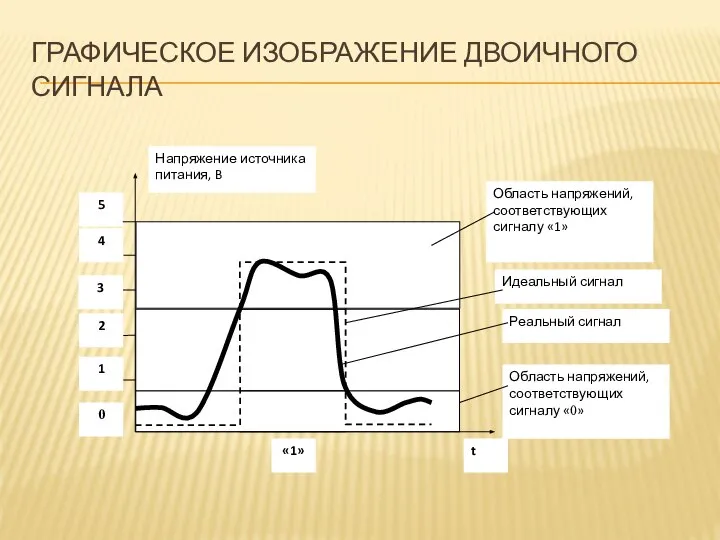
- 5. ГРАФИЧЕСКОЕ ИЗОБРАЖЕНИЕ ДВОИЧНОГО СИГНАЛА
- 6. На рис. показан выходной сигнал такого элемента памяти (например, одного разряда регистра). При изменении его состояний
- 7. Память ЭВМ состоит из конечной последовательности слов, а слова – из конечной последовательности битов. Поэтому объем
- 8. ФОРМЫ ПРЕДСТАВЛЕНИЯ ДВОИЧНЫХ ЧИСЕЛ: - С ФИКСИРОВАННОЙ ЗАПЯТОЙ (ЕСТЕСТВЕННАЯ ФОРМА) - С ПЛАВАЮЩЕЙ ЗАПЯТОЙ (НОРМАЛЬНАЯ ФОРМА)
- 10. например: +195 - целое положительное число -195 - целое отрицательное число +0.125 - правильная положительная дробь
- 12. Двоичные коды числа имеют различные форматы. Формат числа представляет собой совокупность разрядов (разрядную сетку), разделенную на
- 13. 2. ПРЕДСТАВЛЕНИЕ ЦЕЛЫХ ЧИСЕЛ ЦЕЛЫЕ ЧИСЛА БЕЗ ЗНАКА Обычно занимают в памяти компьютера один или два
- 14. ДИАПАЗОН ЗНАЧЕНИЙ ЦЕЛЫХ ЧИСЕЛ БЕЗ ЗНАКА
- 15. 7210 В ОДНОБАЙТОВОМ И ДВУБАЙТОВОМ ФОРМАТЕ
- 16. ЦЕЛЫЕ ЧИСЛА СО ЗНАКОМ ЦЕЛЫЕ ЧИСЛА СО ЗНАКОМ ОБЫЧНО ЗАНИМАЮТ В ПАМЯТИ КОМПЬЮТЕРА ОДИН, ДВА ИЛИ
- 17. В цифровых автоматах применяются три формы записи (кодирования) целых чисел со знаком: прямой, дополнительный, обратный код.
- 18. ПРЯМОЙ КОД Прямой n-разрядный код отличается от двоичного тем, что в нем отводится один, как правило,
- 19. ПРИМЕРЫ (ПРЯМОЙ КОД) 110 00000001 12710 01111111 -110 10000001 -12710 11111111
- 20. ДЛЯ ПРЯМОГО КОДА СПРАВЕДЛИВО СЛЕДУЮЩЕЕ СООТНОШЕНИЕ:
- 21. ДОПОЛНИТЕЛЬНЫЙ КОД. Использование чисел со знаком (прямого кода представления чисел) усложняет структуру ЭВМ. В этом случае
- 22. Смысл перевода отрицательных чисел из прямого в дополнительный и обратный коды поясним на примере с десятичными
- 23. Учитывая, что вычисления проводятся на устройстве с двумя десятичными разрядами, конечный результат будет равен 52. Равенство
- 24. ЕСТЬ ПРОСТОЕ ПРАВИЛО ПОЛУЧЕНИЯ ДОПОЛНЕНИЯ ДВОИЧНЫХ ЧИСЕЛ: Получить инверсию заданного числа (все 0 заменить на 1,
- 25. 0 000 0010 1100 0101 число 1 111 1101 0011 1010 инверсия числа 1 111 1101
- 26. Так как перенос из старшего разряда не учитывается, то результат суммирования равен 0, что подтверждает правильность
- 27. ДЛЯ ДОПОЛНИТЕЛЬНОГО КОДА СПРАВЕДЛИВО СЛЕДУЮЩЕЕ СООТНОШЕНИЕ:
- 28. ОБРАТНЫЙ КОД Для представления отрицательных чисел используется также обратный код, который получается инвертированием всех цифр двоичного
- 29. ПРИМЕРЫ 1) Число: -1 Код модуля числа: 00000001 Обратный код числа: 11111110 2) Число: -127 Код
- 30. ДЛЯ ОБРАТНОГО КОДА СПРАВЕДЛИВО СООТНОШЕНИЕ:
- 31. Таким образом, положительные числа в прямом, обратном и дополнительном кодах изображаются одинаково – двоичными кодами с
- 33. Скачать презентацию





























 Модель жизненного цикла программного обеспечения Build and fix
Модель жизненного цикла программного обеспечения Build and fix Базовые структуры алгоритмов (продолжение)
Базовые структуры алгоритмов (продолжение) Информация: свойства, виды, информация и данные; общая характеристика процесса сбора, передачи, обработки информации
Информация: свойства, виды, информация и данные; общая характеристика процесса сбора, передачи, обработки информации Список типовых блоков сайта
Список типовых блоков сайта Ключевые слова
Ключевые слова CodeEvening. Web-разработка
CodeEvening. Web-разработка Электронные таблицы. Обработка числовой информации в электронных таблицах
Электронные таблицы. Обработка числовой информации в электронных таблицах Компьютетрные объекты
Компьютетрные объекты Requesting Access - BW Reports (Operations Dashboard)
Requesting Access - BW Reports (Operations Dashboard) Adobe InDesign. Быстрое погружение
Adobe InDesign. Быстрое погружение Спрашивай взрослых
Спрашивай взрослых Обработка изображений в системах управления. Методы восстановления изображений. Лекция 7
Обработка изображений в системах управления. Методы восстановления изображений. Лекция 7 Информационно-поисковая система. Современные алгоритмы работы с информацией
Информационно-поисковая система. Современные алгоритмы работы с информацией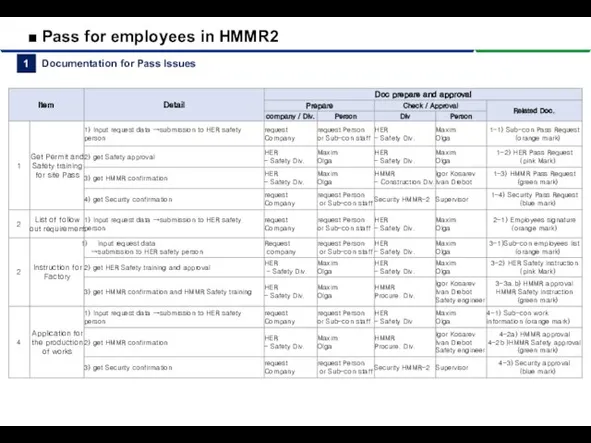 Site pass issue process and instruction
Site pass issue process and instruction Кодирование графической информации
Кодирование графической информации ИК Базы данных. Урок 1
ИК Базы данных. Урок 1 Вещественно-энергетическая картина мира. История вычислительной техники
Вещественно-энергетическая картина мира. История вычислительной техники 314835
314835 Сетевые технологии
Сетевые технологии Язык программирования Java
Язык программирования Java Программирование на языке Python. Алгоритм и его свойства
Программирование на языке Python. Алгоритм и его свойства Основные понятия информационных систем, банков и баз данных. Виды учетов в ОВД
Основные понятия информационных систем, банков и баз данных. Виды учетов в ОВД Powering A Smarter World. Cloud Application
Powering A Smarter World. Cloud Application Информационные процессы. Информация в жизни человека. Понятие информационных ресурсов. Роль информационных ресурсов в развитии
Информационные процессы. Информация в жизни человека. Понятие информационных ресурсов. Роль информационных ресурсов в развитии Актуальные проблемы информатизации образования Материал подготовила: учитель английского языка высшей категории Ведь
Актуальные проблемы информатизации образования Материал подготовила: учитель английского языка высшей категории Ведь  Компьюьерная память
Компьюьерная память База данных – основа информационной системы
База данных – основа информационной системы Презентация на тему Угрозы безопасности информации, их виды
Презентация на тему Угрозы безопасности информации, их виды