Представление вещественных чисел в двоичном коде (10 класс)

Терминология
Нормализованная форма числа – представление числа в виде произведения мантиссы на степень числа 10.
Мантисса – представление числа в виде дроби, целая часть которой находится в интервале [1;10).
Порядок – показатель степени числа 10, при котором произведение этой степени на мантиссу равно исходному числу.

Точность представления чисел
Представление вещественного числа в виде двоичного числа принято называть представлением в формате с плавающей запятой.
Различают:
числа одинарной точности – представление вещественного числа в формате 32-разрядного двоичного числа;
числа двойной точности – представление вещественного числа в формате 64-разрядного двоичного числа.

Кодовое представление числа
31 30 23 22 0

Кодовое представление числа
31 30 23 22 0
Знак

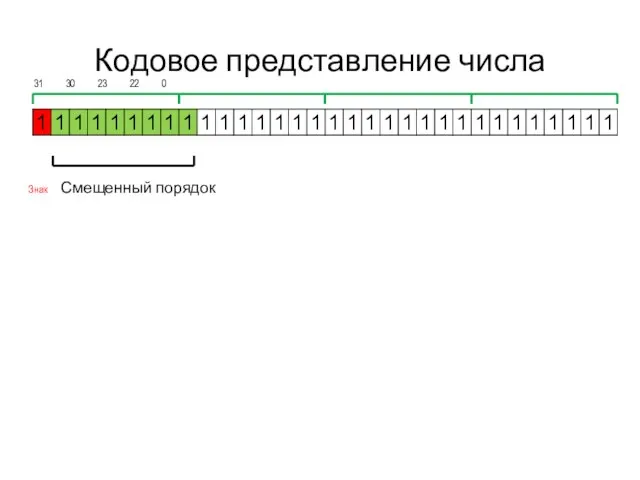
Кодовое представление числа
31 30 23 22 0
Знак Смещенный порядок

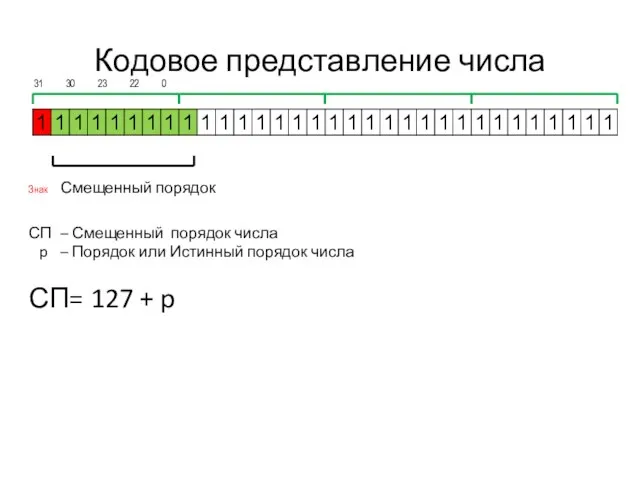
Кодовое представление числа
31 30 23 22 0
СП – Смещенный порядок числа
p – Порядок или Истинный порядок числа
СП= 127 + p
Знак Смещенный порядок

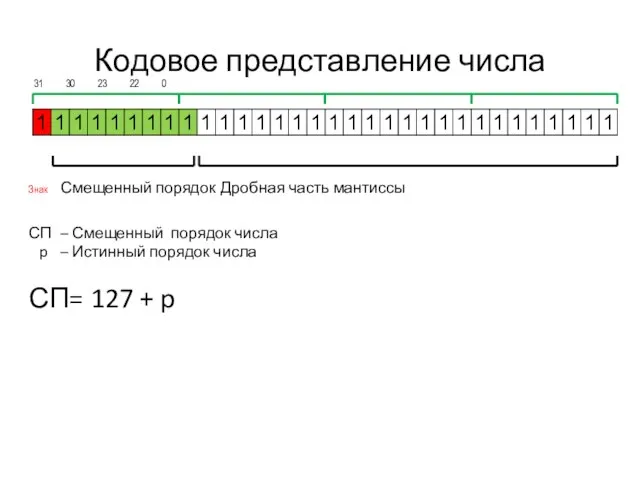
Кодовое представление числа
31 30 23 22 0
Знак Смещенный порядок Дробная часть мантиссы
СП – Смещенный порядок числа
p – Истинный порядок числа
СП= 127 + p

Условности
Число представляется в виде ±m•10±p, где
m (1≤m<10) – мантисса и р – порядок
Чтобы не хранить знак порядка, принято использовать «смещенный порядок» СП=p+127
В двоичной арифметике целая часть m всегда «1», поэтому эту «1» принято «выбрасывать» из двоичного кода числа. (Правило не касается числа «ноль».)
Число «ноль» – принято изображать числом со СП=00000000, т.е. числом из 32-х «0»
Понятие «∞» – принято изображать числом со СП=11111111
Числа из 32-х «1» не существует – переполнение разрядной сетки

Порядок перевода числа из формата с плавающей запятой
Перевести число из шестнадцатиричной системы счисления в двоичную.
Определить знак числа по старшему биту.
Выделить порядок числа из смещенного.
Определить мантиссу числа по дробной части.
Составить нормализованную форму двоичного числа.
Переписать двоичное число в «обычном» представлении.
Перевести число в десятичную систему счисления.

Пример №1
С 1 4 8 0 0 0 0
Определить, какое число задано кодом С148000016

Пример №1
С 1 4 8 0 0 0 0
Знаковый бит «1» показывает, что число отрицательное.
Определить, какое число задано кодом С148000016

Пример №1
С 1 4 8 0 0 0 0
Знаковый бит «1» показывает, что число отрицательное.
Порядок СП=100000102 = 130
Определить, какое число задано кодом С148000016

Пример №1
С 1 4 8 0 0 0 0
Знаковый бит «1» показывает, что число отрицательное.
Порядок СП=100000102 = 130
р = 130 – 127 = 3
Определить, какое число задано кодом С148000016

Пример №1
С 1 4 8 0 0 0 0
Знаковый бит «1» показывает, что число отрицательное.
Порядок СП=100000102 = 130
р = 130 – 127 = 3
Мантисса: m= 1,100 1000 0000 0000 0000 00002
Определить, какое число задано кодом С148000016

Пример №1
С 1 4 8 0 0 0 0
Знаковый бит «1» показывает, что число отрицательное.
Порядок СП=100000102 = 130
р = 130 – 127 = 3
Мантисса: m= 1,100 1000 0000 0000 0000 00002
– 1,10012•1023= – 1100,12 = – 12,5
Определить, какое число задано кодом С148000016

Пример №1
С 1 4 8 0 0 0 0
Знаковый бит «1» показывает, что число отрицательное.
Порядок СП=100000102 = 130
р = 130 – 127 = 3
Мантисса: m= 1,100 1000 0000 0000 0000 00002
– 1,10012•1023= – 1100,12 = – 12,5
Определить, какое число задано кодом С148000016
Ответ: –12,5

Задачи
Определить, какое число задано кодом С334000016?
Определить, какое число задано кодом С1СD000016?
Определить, какое число задано кодом 41СA000016?

Домашнее задание №1
Записать в тетрадь:
тему презентации;
определения понятий: нормализованная форма числа, порядок, мантисса, формат с плавающей запятой;
алгоритм перевода числа из Формата с Плавающей Запятой (ФПЗ);
пример перевода числа из ФПЗ;
решения задач №2 и №3 со слайда «Задачи».

Порядок перевода числа в формат с плавающей запятой
Перевести модуль числа из десятичной системы счисления в двоичную.
Представить двоичное число в нормализованной форме.
Рассчитать смещённый порядок числа.
Разместить знак числа, порядок и мантиссу в соответствующие разряды сетки.
Перевести полученное число в шестнадцатиричную систему счисления

Пример №2
1)Т.к. число отрицательное, то знаковый бит «1».
Определить 16-ричное представление числа -35,25

Пример №2
1)Т.к. число отрицательное, то знаковый бит «1».
Определить 16-ричное представление числа -35,25
2) 35,25 = 32 + 3 + 0,25 = 10 00002 + 112 + 0,012 = 10 0011,012
3) 10 0011,012 = 1,0001 1012 • 1025
4) Порядок p = 5 ⇒ СП=5+127=4+128=1000 01002

Пример №2
1)Т.к. число отрицательное, то знаковый бит «1».
2) 35,25 = 32 + 3 + 0,25 = 10 00002 + 112 + 0,012 = 10 0011,012
3) 10 0011,012 = 1,0001 1012 • 1025
4) Порядок p = 5 ⇒ СП=5+127=4+128=1000 01002
Определить 16-ричное представление числа -35,25

Пример №2
1)Т.к. число отрицательное, то знаковый бит «1».
2) 35,25 = 32 + 3 + 0,25 = 10 00002 + 112 + 0,012 = 10 0011,012
3) 10 0011,012 = 1,0001 1012 • 1025
4) Порядок p = 5 ⇒ СП=5+127=4+128=1000 01002
Определить 16-ричное представление числа -35,25
5) Мантисса: m= 1,0001 1012
Целая часть 1, отбрасывается, дробная 0001 101 – записывается в разрядную сетку и дополняется «нулями»

Пример №2
1)Т.к. число отрицательное, то знаковый бит «1».
2) 35,25 = 32 + 3 + 0,25 = 10 00002 + 112 + 0,012 = 10 0011,012
3) 10 0011,012 = 1,0001 1012 • 1025
4) Порядок p = 5 ⇒ СП=5+127=4+128=1000 01002
5) Мантисса: m= 1,0001 1012
Целая часть 1, отбрасывается, дробная 0001 101 – записывается в разрядную сетку и дополняется «нулями»
Определить 16-ричное представление числа -35,25

Пример №2
С 2 0 D 0 0 0 0
1)Т.к. число отрицательное, то знаковый бит «1».
2) 35,25 = 32 + 3 + 0,25 = 10 00002 + 112 + 0,012 = 10 0011,012
3) 10 0011,012 = 1,0001 1012 • 1025
4) Порядок p = 5 ⇒ СП=5+127=4+128=1000 01002
5) Мантисса: m= 1,0001 1012
Целая часть 1, отбрасывается, дробная 0001 101 – записывается в разрядную сетку и дополняется «нулями»
Определить 16-ричное представление числа -35,25

Пример №2
С 2 0 D 0 0 0 0
1)Т.к. число отрицательное, то знаковый бит «1».
2) 35,25 = 32 + 3 + 0,25 = 10 00002 + 112 + 0,012 = 10 0011,012
3) 10 0011,012 = 1,0001 1012 • 1025
4) Порядок p = 5 ⇒ СП=5+127=4+128=1000 01002
5) Мантисса: m= 1,0001 1012
Целая часть 1, отбрасывается, дробная 0001 101 – записывается в разрядную сетку и дополняется «нулями»
Определить 16-ричное представление числа -35,25
Ответ: C20D 000016

Задачи
Определить 16-ричное представление 13,375
Определить 16-ричное представление -43,75
Определить 16-ричное представление -123,625