Информация и алфавит

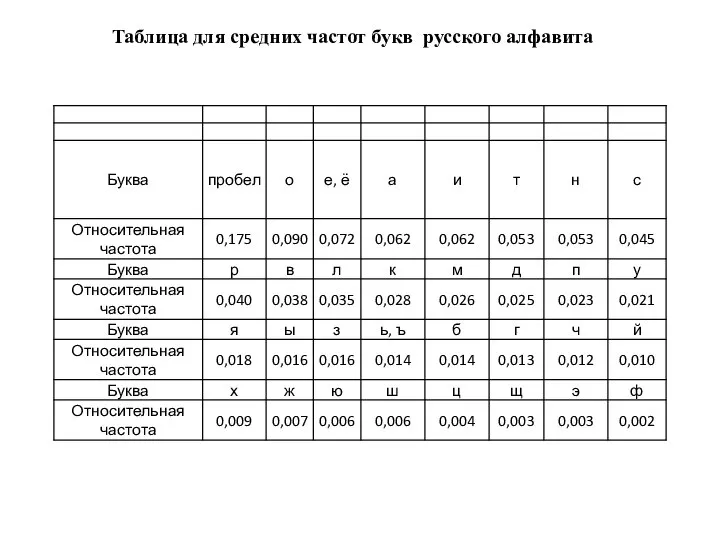
Таблица для средних частот букв русского алфавита

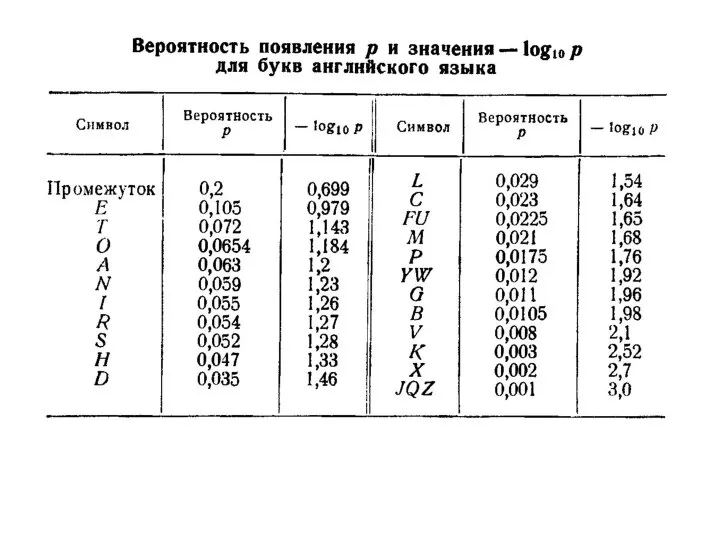
Сообщения, в которых вероятность появления каждого отдельного знака не меняется со временем, называют шенноновскими, а порождающий его отправитель – шенноновским источником.
Если сообщение является шенноновским, то набор знаков и связанная с каждым знаком информация известны заранее.
В этом случае интерпретация сообщения, представляющего собой последовательность сигналов, сводится к задаче распознавания знака, т.е. выявлению какой именно знак находится в данном месте сообщения.

Понятие о кодировании. Коды.
Кодирование символьной информации
Теория кодирования информации является одним из разделов теоретической информатики. К основным задачам, решаемым в данном разделе, необходимо отнести следующие:
разработка принципов наиболее экономичного кодирования информации;
согласование параметров передаваемой информации с особенностями канала связи;
разработка приемов, обеспечивающих надежность передачи информации по каналам связи, т.е. отсутствие потерь информации.

Операции кодирования и декодирования называются обратимыми, если их последовательное применение обеспечивает возврат к исходной информации без каких-либо ее потерь.
Наиболее удобным способом задания кода является табличный способ. Например: пусть имеется алфавит с конечным числом букв: А={a1, a2, a3, a4}. Тогда код для А:
Определения:

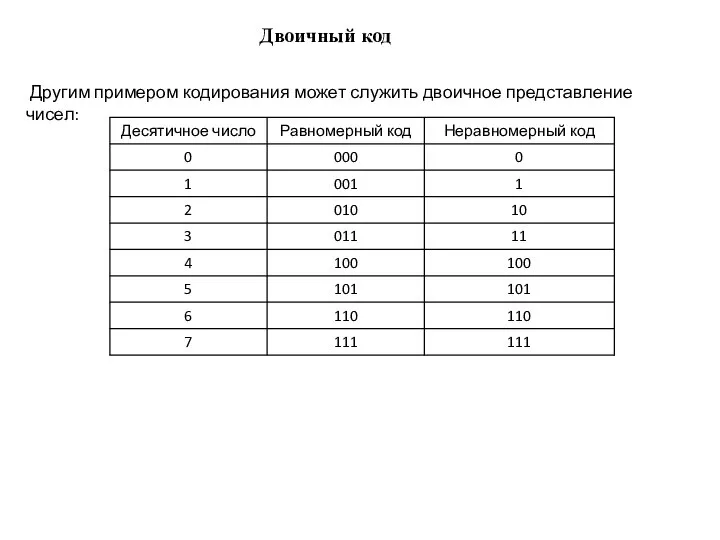
Другим примером кодирования может служить двоичное представление чисел:
Двоичный код

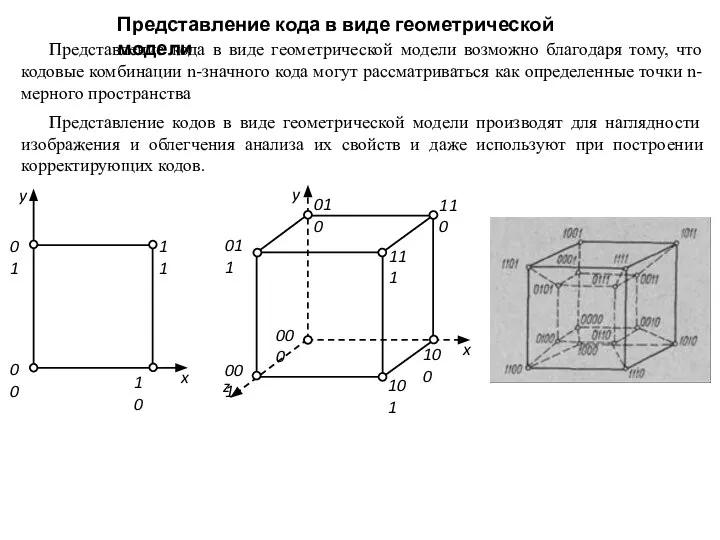
Представление кода в виде геометрической модели
Представление кода в виде геометрической модели возможно благодаря тому, что кодовые комбинации n-значного кода могут рассматриваться как определенные точки n-мерного пространства
Представление кодов в виде геометрической модели производят для наглядности изображения и облегчения анализа их свойств и даже используют при построении корректирующих кодов.

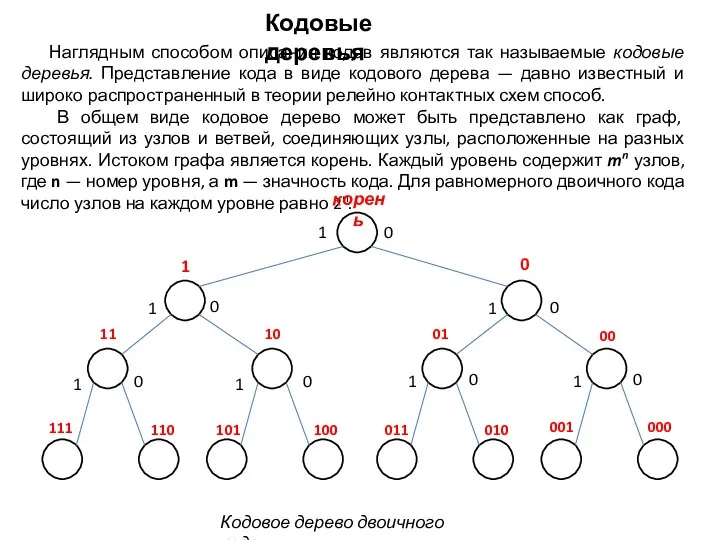
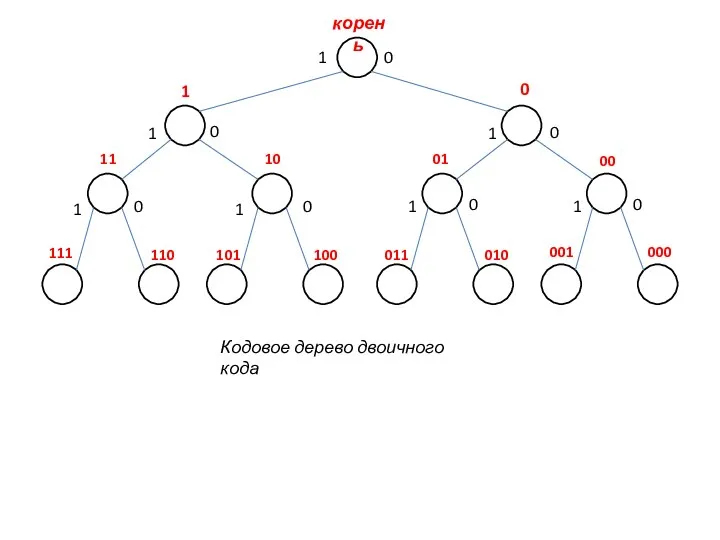
Наглядным способом описания кодов являются так называемые кодовые деревья. Представление кода в виде кодового дерева — давно известный и широко распространенный в теории релейно контактных схем способ.
В общем виде кодовое дерево может быть представлено как граф, состоящий из узлов и ветвей, соединяющих узлы, расположенные на разных уровнях. Истоком графа является корень. Каждый уровень содержит mn узлов, где n — номер уровня, а m — значность кода. Для равномерного двоичного кода число узлов на каждом уровне равно 2n.
Кодовые деревья
корень
1
0
1
0
1
1
1
1
1
1
0
0
0
0
0
0
11
10
01
00
111
110
101
100
011
010
001
000
Кодовое дерево двоичного кода

При помощи кодовых деревьев наглядно представляются коды, обладающие свойством префикса, или префиксные коды, т. е. коды, которые могут быть получены путем последовательного вычеркивания последнего знака кодовой комбинации (ни одна из комбинаций такого кода не может быть префиксом комбинации того же кода). Например, префиксами кодовой комбинации 11101101 будут: 1, 11, 111,1110, 111011, 1110110, 11101101.
То есть для однозначного декодирования кодовой комбинации 11101101 ни один из передаваемых кодов не может быть представлен комбинациями 1, 11, 111, 1110, 111011, 1110110, 11101101.
Если число узлов на каждом уровне кодового дерева равно mn, то дерево называют полным.
Величина D = mk, где k указывает порядок наивысшего уровня кодового дерева, называется объемом дерева.
Объем дерева характеризует число кодовых комбинаций, которое может быть построено при помощи данного дерева.

Префиксом данной кодовой комбинации Аi является любая последовательность, составленная из ее начальной части, включая саму комбинацию Аi
Та часть кодовой комбинации, которая дополняет префикс до самой кодовой комбинации, называется суффиксом, т. е. каждую кодовую комбинацию можно разбить на префикс и соответствующие суффиксы.
Имея кодовое дерево, легко определить, обладает ли данный код свойством префикса. Если ни один узел кодового дерева не является вершиной данного кода, то он обладает свойством префикса. Для заданного кода кодовое дерево всегда одно и то же.
Узлы, которые не соединяются с последующими уровнями, называются оконечными. Комбинации кода, соответствующие оконечным узлам, являются комбинациями кода, обладающего свойством префикса.
Если добавление к комбинациям заданного кода некоторой новой комбинации ведет к нарушению свойства префикса, то такой код называется полным.
Свойство префикса широко используют при построении неравномерных кодов с минимальной длиной кодовых слов, в частности кодовых деревьев по методу Хаффмена

корень
1
0
1
0
1
1
1
1
1
1
0
0
0
0
0
0
11
10
01
00
111
110
101
100
011
010
001
000
Кодовое дерево двоичного кода

Математическая постановка задачи кодирования
Пусть первичный алфавит A содержит N знаков со средней информацией на знак, определенной с учетом вероятностей их появления, I(A). Вторичный алфавит B – M знаков со средней информационной емкостью I(B). Пусть также исходное сообщение, представленное в первичном алфавите, содержит n знаков, а закодированное сообщение – m знаков. Если исходное сообщение содержит Ist(A) информации, а закодированное – Ifin(B), то условие обратимости кодирования, т.е. неисчезновения информации при кодировании, очевидно, может быть записано следующим образом:
Ist(A) ≤Ifin(B)
(1)
(2)

Первая теорема Шеннона о передаче информации, которая называется также основной теоремой о кодировании при отсутствии помех, формулируется следующим образом:
При отсутствии помех передачи всегда возможен такой вариант кодирования сообщения, при котором среднее число знаков кода, приходящихся на один знак кодируемого алфавита, будет сколь угодно близко к отношению средних информаций на знак первичного и вторичного алфавитов.
Данная величина показывает, насколько операция кодирования увеличила длину исходного сообщения.
Используя понятие избыточности кода, можно дать более короткую формулировку теоремы:
При отсутствии помех передачи всегда возможен такой вариант кодирования сообщения, при котором избыточность кода будет сколь угодно близкой к нулю.
(3)
(4)

М=2
При отсутствии помех средняя длина двоичного кода может быть сколь угодно близкой к средней информации, приходящейся на знак первичного алфавита.
При декодировании двоичных сообщений возникает проблема выделения из потока сигналов (последовательности импульсов и пауз) отдельных кодов, соответствующим отдельным знакам первичного алфавита.
При этом приемное устройство фиксирует интенсивность и длительность сигналов.
Применение формулы (4) для двоичных сообщений источника без памяти при кодировании знаками равной вероятности даёт:
(5)
Определение количества переданной информации при двоичном кодировании сводится к простому подсчету числа импульсов (единиц) и пауз (нулей).

Возможны следующие особенности вторичного алфавита:
Элементарные сигналы (0 и 1) могут иметь одинаковые или разные длительности.
Их количество в коде (длина кодовой цепочки), который ставится в соответствие знаку первичного алфавита, также может быть одинаковым (в этом случае код называется равномерным) или разным (неравномерный код).
Коды могут строиться для каждого знака исходного алфавита (алфавитное кодирование) или для их комбинаций (кодирование блоков, слов).
В случае использования неравномерного кодирования или сигналов разной длительности (ситуации (2), (3) и (4)) для отделения кода одного знака от другого между ними необходимо передавать специальный сигнал – временной разделитель (признак конца знака) или применять такие коды, которые оказываются уникальными, т.е. несовпадающими с частями других кодов. При равномерном кодировании одинаковыми по длительности сигналами (ситуация (1)) передачи специального разделителя не требуется, поскольку отделение одного кода от другого производится по общей длительности, которая для всех кодов оказывается одинаковой (или одинаковому числу бит при хранении).

Алфавитное неравномерное двоичное кодирование сигналами равной длительности
построить такую систему кодирования, чтобы суммарная длительность кодов при передаче (или суммарное число кодов при хранении) данного сообщения была бы наименьшей
00100010000111010101110000110
Использовать специальную комбинацию элементарных сигналов, которая интерпретируется декодером как разделитель знаков
Применение префиксных кодов

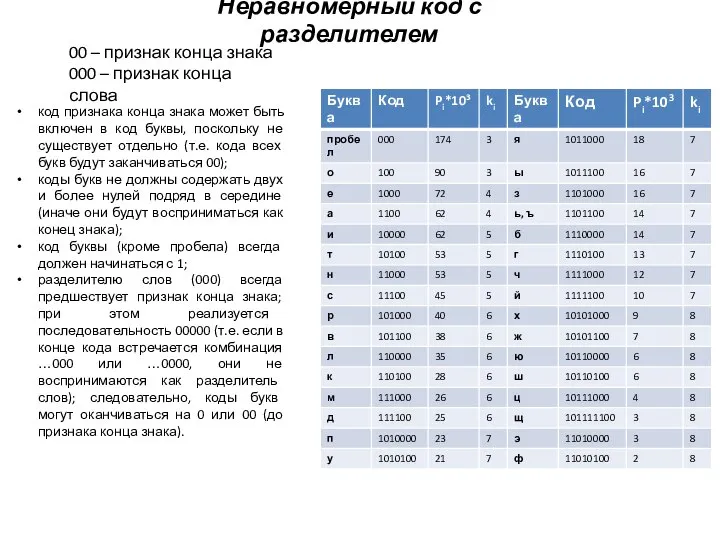
Неравномерный код с разделителем
00 – признак конца знака
000 – признак конца слова
код признака конца знака может быть включен в код буквы, поскольку не существует отдельно (т.е. кода всех букв будут заканчиваться 00);
коды букв не должны содержать двух и более нулей подряд в середине (иначе они будут восприниматься как конец знака);
код буквы (кроме пробела) всегда должен начинаться с 1;
разделителю слов (000) всегда предшествует признак конца знака; при этом реализуется последовательность 00000 (т.е. если в конце кода встречается комбинация …000 или …0000, они не воспринимаются как разделитель слов); следовательно, коды букв могут оканчиваться на 0 или 00 (до признака конца знака).

Поскольку для русского языка, I1(r)=4,356 бит, избыточность данного кода, согласно, составляет:
Q(r) = 4,356/4,964 - 1 ≈0,122
Это означает, что при данном способе кодирования будет передаваться приблизительно на 12% больше информации, чем содержит исходное сообщение. Аналогичные вычисления для английского языка дают значение K(e, 2) = 4,716, что при I1(e) = 4,036 бит приводят к избыточности кода Q(e,2)= 0,168.

Оптимальное кодирование. Префиксные коды
Оптимальным кодированием называется процедура преобразования символов первичного алфавита т: в кодовые слова во вторичном алфавите m1, при которой средняя длина сообщений во вторичном алфавите имеет минимально возможную для данного m2 длину.
Оптимальными называются коды, представляющие кодируемые понятия кодовыми словами минимальной средней длины.
В сообщениях, составленных из кодовых слов оптимального кода, статистическая избыточность сведена к минимуму, в идеальном случае — к нулю.
Основные свойства оптимальных кодов:
минимальная средняя длина кодового слова оптимального кода обеспечивается в том случае, когда избыточность каждого кодового слова сведена к минимуму (в идеальном случае — к нулю);
кодовые слова оптимального кода должны строиться из равновероятных и взаимонезависимых символов.

Неравномерный код может быть однозначно декодирован, если никакой из кодов не совпадает с началом (префиксом) какого-либо иного более длинного кода.
Например, если имеется код 110, то уже не могут использоваться коды 1, 11, 1101, 110101 и пр. Если условие Фано выполняется, то при прочтении (расшифровке) закодированного сообщения путем сопоставления со списком кодов всегда можно точно указать, где заканчивается один код и начинается другой.
Префиксные коды
Условие Фано:

а л м р у ы
10 010 00 11 0110 0111
Пример
00100010000111010101110000110
Отрезать от текущего сообщения крайний левый символ, присоединить к рабочему кодовому слову.
Сравнить рабочее кодовое слово с кодовой таблицей; если совпадения нет, перейти к (1).
Декодировать рабочее кодовое слово, очистить его.
Проверить, имеются ли еще знаки в сообщении; если "да", перейти к (1).
Применение данного алгоритма даёт:

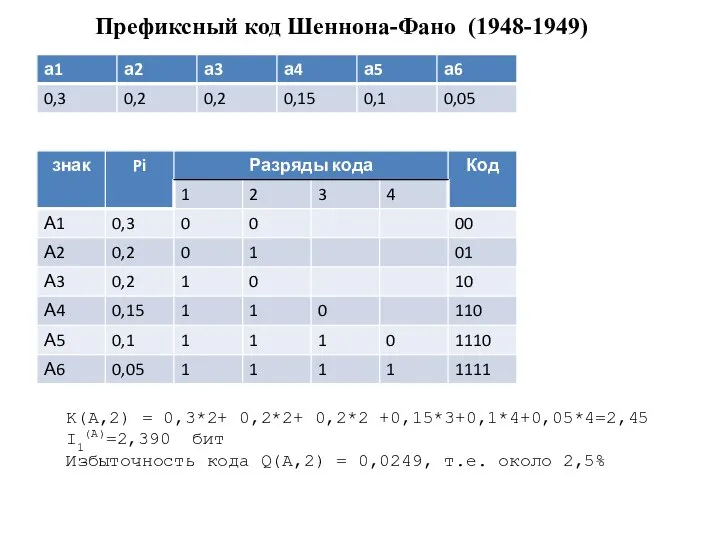
Построение оптимального кода по методу Шеннона — Фано для сообщений сводится к следующей процедуре:
множество из М сообщений располагают в порядке убывания вероятностей;
первоначальный ансамбль кодируемых сигналов разбивают на две группы таким образом, чтобы суммарные вероятности сообщений обеих групп были по возможности равны;
первой группе присваивают символ 0, второй группе — символ 1;
каждую из подгрупп делят на две группы так, чтобы их суммарные вероятности были по возможности равны;
первым подгруппам каждой из групп вновь присваивают О, а вторым — 1, в результате чего получают вторые цифры кода. Затем каждую из четырех подгрупп вновь делят на равные (с точки зрения суммарной вероятности) части и т. д. до тех пор, пока в каждой из подгрупп останется по одной букве.

Префиксный код Шеннона-Фано (1948-1949)
K(A,2) = 0,3*2+ 0,2*2+ 0,2*2 +0,15*3+0,1*4+0,05*4=2,45
I1(A)=2,390 бит
Избыточность кода Q(A,2) = 0,0249, т.е. около 2,5%

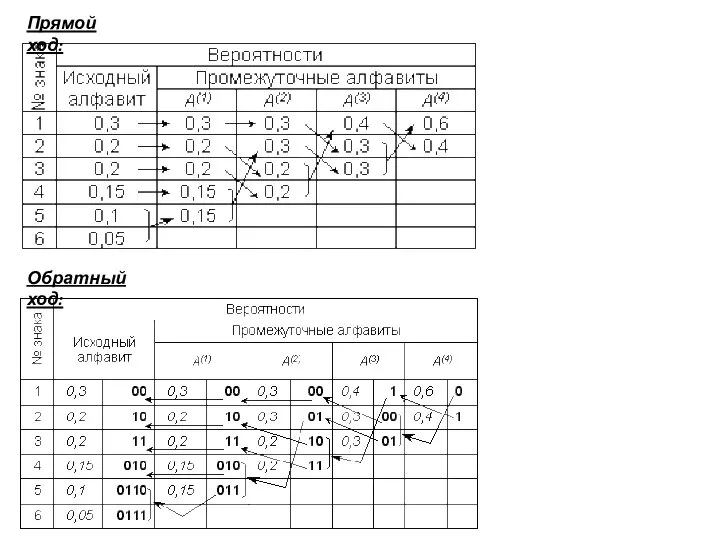
Префиксный код Хаффмана
Пример тот же.
Алгоритм:
Создадим новый вспомогательный алфавит A1, объединив два знака с наименьшими вероятностями (a5 и a6) и заменив их одним знаком (например, a(1));
Вероятность нового знака будет равна сумме вероятностей тех, что в него вошли, т.е. 0,15;
Остальные знаки исходного алфавита включим в новый без изменений; общее число знаков в новом алфавите, очевидно, будет на 1 меньше, чем в исходном.
Аналогичным образом продолжим создавать новые алфавиты, пока в последнем не останется два знака; ясно, что число таких шагов будет равно N – 2, где N – число знаков исходного алфавита (в нашем случае N = 6, следовательно, необходимо построить 4 вспомогательных алфавита). В промежуточных алфавитах каждый раз будем переупорядочивать знаки по убыванию вероятностей.

Прямой ход:
Обратный ход:

Средняя длина кода оказывается равной K(2) = 4,395; избыточность кода
Q(r) = 0,00887, т.е. менее 1%.
Таким образом, можно заключить, что существует метод построения оптимального неравномерного алфавитного кода.
Метод Хаффмана и его модификация – метод адаптивного кодирования (динамическое кодирование Хаффмана) – нашли широчайшее применение в программах-архиваторах, программах резервного копирования файлов и дисков, в системах сжатия информации в модемах и факсах

Код Хемминга. Построение дерева алфавитов

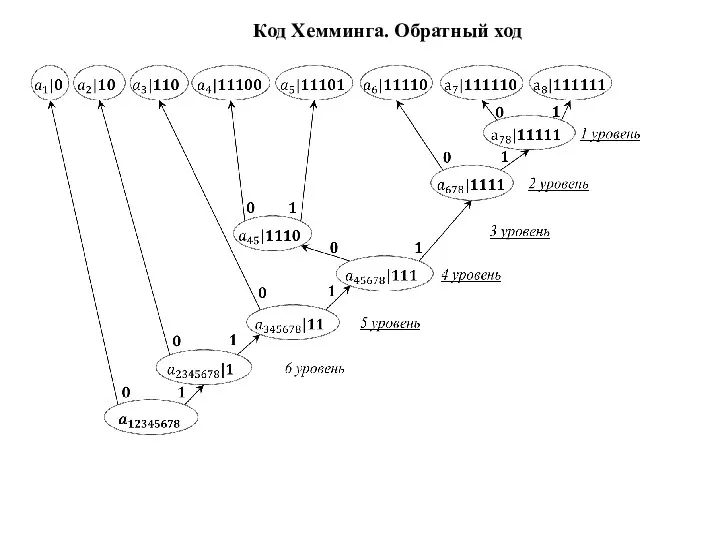
Код Хемминга. Обратный ход

Равномерное алфавитное двоичное кодирование. Байтовый код
В этом случае двоичный код первичного алфавита строится цепочками равной длины, т.е. со всеми знаками связано одинаковое количество информации равное I0.
Передавать признак конца знака не требуется, поэтому для определения длины кодовой цепочки можно воспользоваться формулой: K(2) = log2N.
Приемное устройство просто отсчитывает оговоренное заранее количество элементарных сигналов и интерпретирует цепочку (устанавливает, какому знаку она соответствует).
Правда, при этом недопустимы сбои, например, пропуск одного элементарного сигнала приведет к сдвигу всей кодовой последовательности и неправильной ее интерпретации; решается проблема путем синхронизации передачи или иными способами.
С другой стороны, применение равномерного кода оказывается одним из средств контроля правильности передачи, поскольку факт поступления лишнего элементарного сигнала или, наоборот, поступление неполного кода сразу интерпретируется как ошибка.