Преобразование логических выражений

Задача 1.
ИНФОРМАТИКА
2014г. Кирсанов Илья Андреевич ©
Для какого из названий животных ложно высказывание:
(Заканчивается на согласную букву) Λ (B слове 6 букв) → (Четвертая буква согласная)?
1) Страус
2) Леопард
3) Верблюд
4) Кенгуру
Решение1. (Заканчивается на согласную букву) Λ (B слове 6 букв) → (Четвертая буква согласная)=0, значит отрицание этого высказывания истинно. Возьмём отрицание:
(Заканчивается на согласную букву) Λ (B слове 6 букв) Λ (Четвертая буква гласная)=1. Подходит только первый вариант.

Задача 1.
ИНФОРМАТИКА
2014г. Кирсанов Илья Андреевич ©
Решение2. В первую очередь выполняется логическое "И".
Импликация ложна только тогда, когда посылка истина, а следствие ложно.
Посылка {(Заканчивается на согласную букву) Λ (B слове 6 букв)} истина для варианта один, а следствие {(Четвертая буква согласная)} для него ложно. Следовательно, ответ 1.
Ответ 1

Задача 2.
ИНФОРМАТИКА
2014г. Кирсанов Илья Андреевич ©
Логическое выражение ¬Y V ¬((Х V Y) Λ ¬Y) Λ Х Λ ¬Y максимально упpощаетcя до выражения
1) Х Λ Y
2) ¬Y
3) Х
4) 1
Решение.
Рассмотрим выражение в скобках:
¬((Х V Y) Λ ¬Y) = (¬(Х V Y) V Y) = (¬(Х V Y) V Y)= ¬Х Λ ¬Y V Y
Подставим в исходное выражение:
¬Y V (¬Х Λ ¬Y V Y )Λ Х Λ ¬Y= ¬Y V (¬Х Λ ¬Y Λ Х Λ ¬Y) V (Y Λ Х Λ ¬Y)
Обе скобки в последнем выражении содержат Y Λ ¬Y, что всегда ложно, ¬Y V 0 V0= ¬Y
Ответ 2

Задача 3.
ИНФОРМАТИКА
2014г. Кирсанов Илья Андреевич ©
На числовой прямой даны три отрезка: P = [20,50],
Q = [15, 20] и R=[40,80]. Выберите такой отрезок A, что формула
((x ∈ P) → (x ∈ Q)) ∨ ((x ∈ A)→ (x ∈ R))
тождественно истинна, то есть принимает значение 1 при любом значении переменной х.
1) [10,25]
2) [20, 30]
3) [40,50]
4) [35, 45]

Задача 3.
ИНФОРМАТИКА
2014г. Кирсанов Илья Андреевич ©
В этой задаче нужно, чтобы отрезок А перекрывал недостающие значения. Преобразуем выражение к стандартным операциям:
((x ∈ P) → (x ∈ Q)) ∨ ((x ∈ A)→ (x ∈ R))=
=((x ∈ P) V (x ∈ Q)) ∨ ((x ∈ A)V (x ∈ R))=1
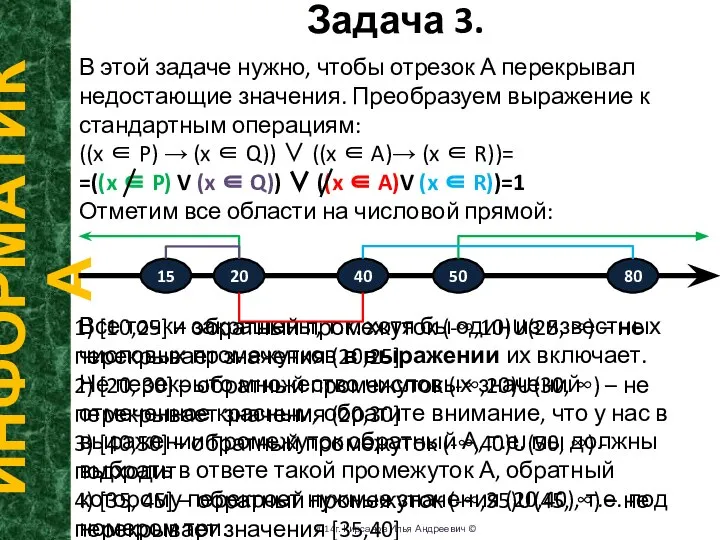
Отметим все области на числовой прямой:
Все точки закрашены, т.к. хотя бы один из известных числовых промежутков в выражении их включает.
Не перекрыто множество числовых значений отмеченное красным, обратите внимание, что у нас в выражении промежуток обратный А, т.е. мы должны выбрать в ответе такой промежуток А, обратный которому перекроет нужные значения (20,40), т.е. под номером три.
1) [10,25] – обратный промежуток (-∞,10)U(25, ∞) – не перекрывает значения (20,25]
2) [20, 30] – обратный промежуток (-∞,20)U(30, ∞) – не перекрывает значения (20,30]
3) [40,50] – обратный промежуток (-∞,40)U(50, ∞) - подходит
4) [35, 45] – обратный промежуток (-∞,35)U(45, ∞) – не перекрывает значения [35,40]
Ответ 3

Задача 4.
ИНФОРМАТИКА
2014г. Кирсанов Илья Андреевич ©
На числовой прямой даны три отрезка: P = [10,15], Q = [10,20] и R=[5,15]. Выберите такой интервал A, что формулы
(x ∈ A) → (x ∈ P) и (x ∈ Q) → (x ∈ R)
тождественно равны, то есть принимают равные значения при любом значении переменной х (за исключением, возможно, конечного числа точек).
1) [5, 12]
2) [10, 17]
3) [12, 20]
4) [15, 25]
Решение. Преобразуем выражения:
(x ∈ A) → (x ∈ P) = (x ∈ A) V (x ∈ P)
(x ∈ Q) → (x ∈ R)= (x ∈ Q) V (x ∈ R)
Затем построим две прямые, и отметим на каждой свои промежутки.

Задача 4.
ИНФОРМАТИКА
2014г. Кирсанов Илья Андреевич ©
(x ∈ A) V (x ∈ P)
(x ∈ Q) V (x ∈ R)
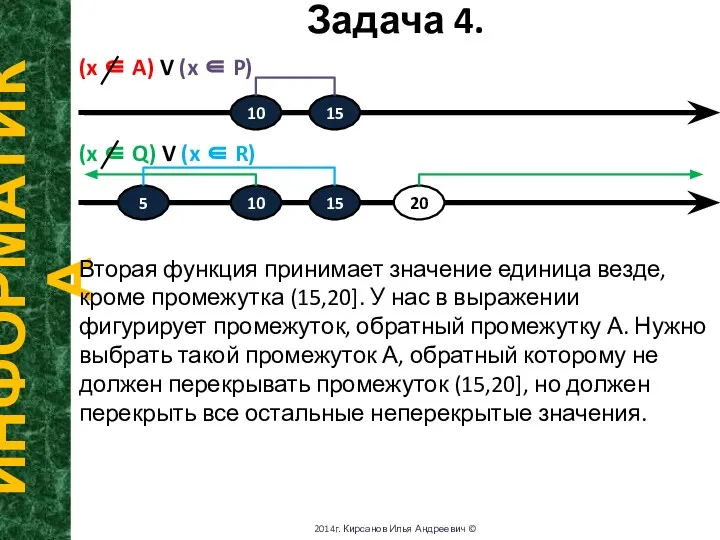
Вторая функция принимает значение единица везде, кроме промежутка (15,20]. У нас в выражении фигурирует промежуток, обратный промежутку А. Нужно выбрать такой промежуток А, обратный которому не должен перекрывать промежуток (15,20], но должен перекрыть все остальные неперекрытые значения.
5
20
15
10
10
15

Задача 4.
ИНФОРМАТИКА
2014г. Кирсанов Илья Андреевич ©
(x ∈ A) V (x ∈ P)
(x ∈ Q) V (x ∈ R)
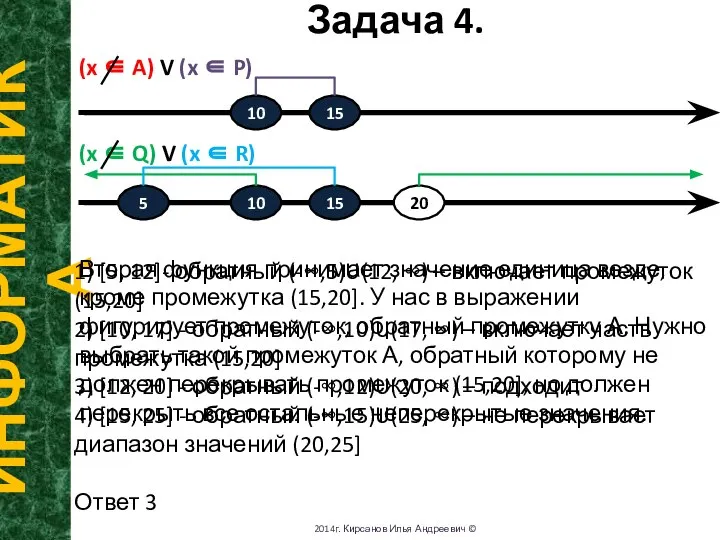
Вторая функция принимает значение единица везде, кроме промежутка (15,20]. У нас в выражении фигурирует промежуток, обратный промежутку А. Нужно выбрать такой промежуток А, обратный которому не должен перекрывать промежуток (15,20], но должен перекрыть все остальные неперекрытые значения.
5
20
15
10
10
15
1) [5, 12]- обратный (-∞,5)U(12, ∞) – включает промежуток (15,20]
2) [10, 17] - обратный (-∞,10)U(17, ∞) – включает часть промежутка (15,20]
3) [12, 20] - обратный (-∞,12)U(20, ∞) – подходит
4) [15, 25] - обратный (-∞,15)U(25, ∞) – не перекрывает диапазон значений (20,25]
Ответ 3

Вопросы.
ИНФОРМАТИКА
2014г. Кирсанов Илья Андреевич ©
На числовой прямой даны два отрезка: Р = [40, 60] и Q = [20, 90]. Выберите такой отрезок А, чтобы формула
((x ∈ P) → (x ∈ A)) ∧ ((x ∈ A) → (x ∈ Q))
была тождественно истинна, то есть принимала значение 1 при любом значении переменной х. Если таких отрезков несколько, укажите тот, который имеет меньшую длину.
1) [17, 43]
2) [17, 73]
3) [37, 53]
4) [37, 63]
Ответ 4