Содержание
- 2. Структурное программирование на языке Си Тема 1. Теория © К.Ю. Поляков, 2007-2009
- 3. Этапы разработки программ Постановка задачи определить цель и категорию программы (системная, прикладная) определить исходные данные и
- 4. Этапы разработки программ Разработка модели данных формальная модель типы данных (массивы, структуры, …) взаимосвязь между данными
- 5. Этапы разработки программ Тестирование программы (проверка на исходных данных, для которых известен результат) альфа-тестирование: внутри фирмы
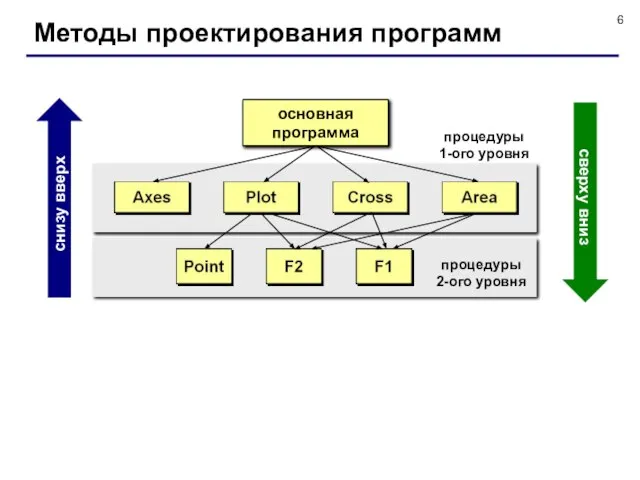
- 6. Методы проектирования программ основная программа процедуры 1-ого уровня процедуры 2-ого уровня снизу вверх сверху вниз
- 7. Проектирование «снизу вверх» сначала составляются процедуры нижнего уровня, из которых затем «собираются» процедуры более высокого уровня.
- 8. Проектирование «сверху вниз» метод последовательного уточнения: начинаем с основной программы; она разбивается на подзадачи, для каждой
- 9. Структурное программирование Существовавшие проблемы: увеличилась сложность программ сократилось время на разработку Цели: повысить надежность уменьшить время
- 10. Структурное программирование Принципы: абстракции: программу можно рассматривать на любом уровне без лишних подробностей модульности: программа разбивается
- 11. Модуль Модуль – это программный блок (процедура или функция), отделенный от кода других модулей, который полностью
- 12. Оформление текста программы Шапка – комментарий в начале процедур и функций. //---------------------------------------- // Sum сумма элементов
- 13. Оформление текста программы Отступы – тело цикла, условного оператора, оператора выбора и т.п. сдвигается вправо на
- 14. Оформление текста программы «говорящие» имена функций, процедур, переменных: Sum, ShowMenu, count, speed. пробелы в операторах выделение
- 15. Структурное программирование на языке Си Тема 2. Проект © К.Ю. Поляков, 2007-2009
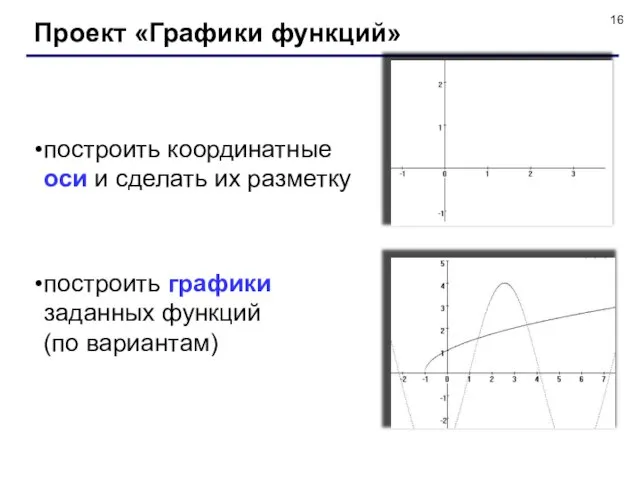
- 16. Проект «Графики функций» построить координатные оси и сделать их разметку построить графики заданных функций (по вариантам)
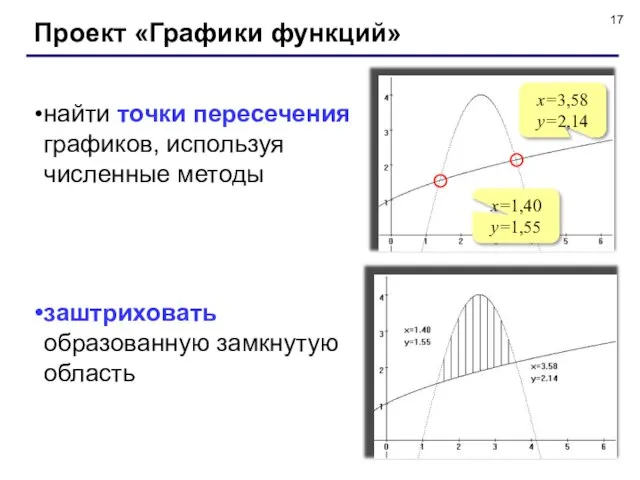
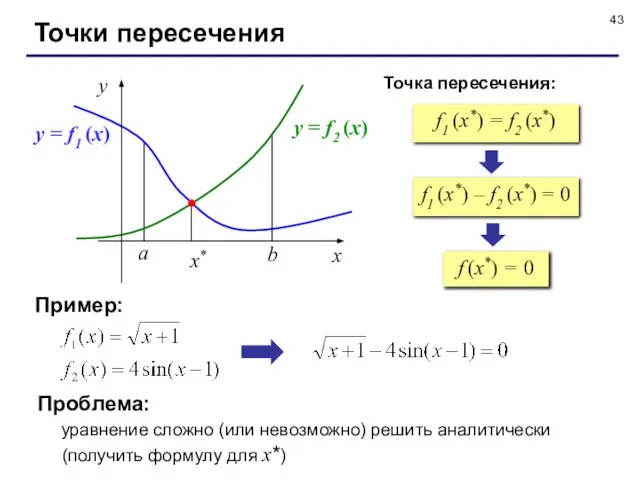
- 17. Проект «Графики функций» найти точки пересечения графиков, используя численные методы заштриховать образованную замкнутую область x=3,58 y=2,14
- 18. Проект «Графики функций» вычислить площадь этой области двумя способами оформить отчет по работе S1=3,014 S2=3,025
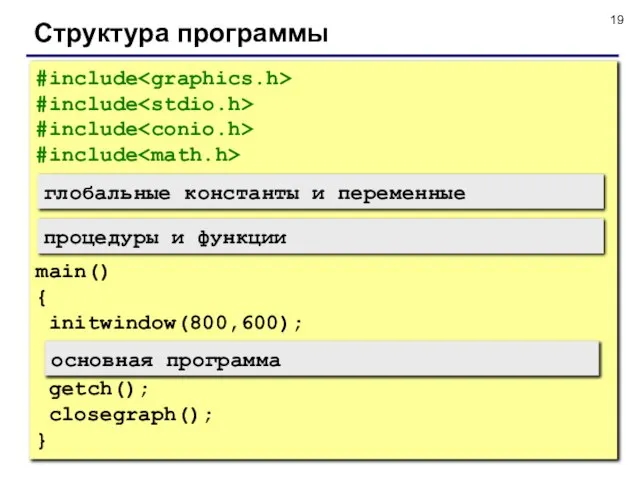
- 19. Структура программы #include #include #include #include main() { initwindow(800,600); getch(); closegraph(); } глобальные константы и переменные
- 20. Разбивка программы на этапы Axes(); // оси координат Plot(); // графики функций Cross(); // точки пересечения
- 21. Структурное программирование на языке Си Тема 3. Графики функций © К.Ю. Поляков, 2007-2009
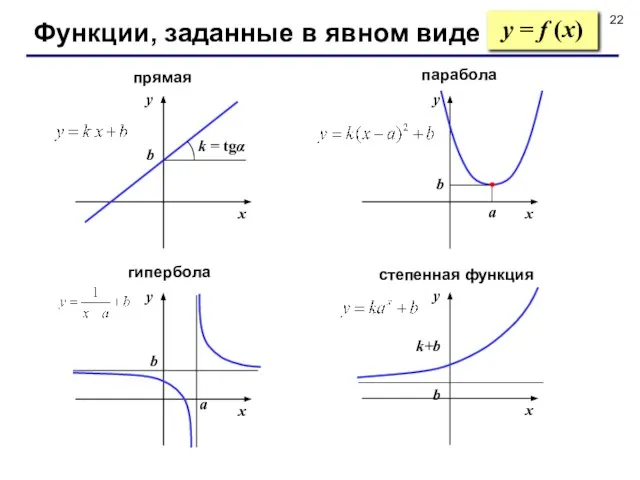
- 22. Функции, заданные в явном виде y = f (x)
- 23. Функции, заданные в неявном виде f (x, y) = 0 пример: уравнение эллипса
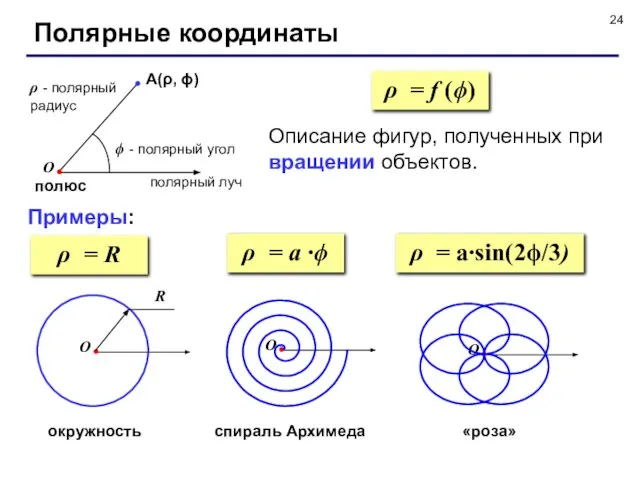
- 24. полюс Полярные координаты А(ρ, ϕ) ϕ - полярный угол ρ - полярный радиус Примеры: Описание фигур,
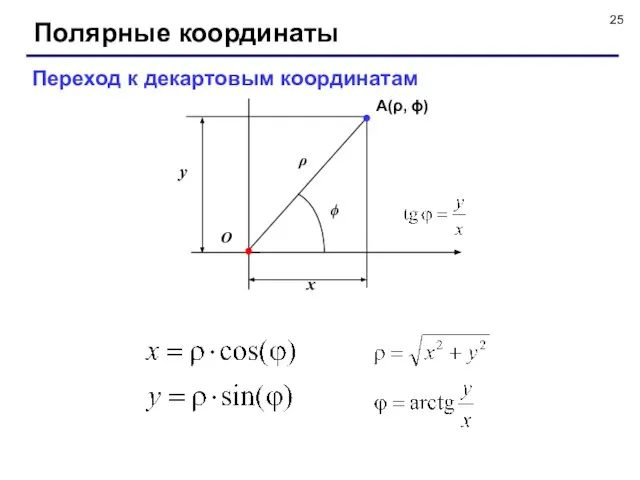
- 25. Полярные координаты Переход к декартовым координатам
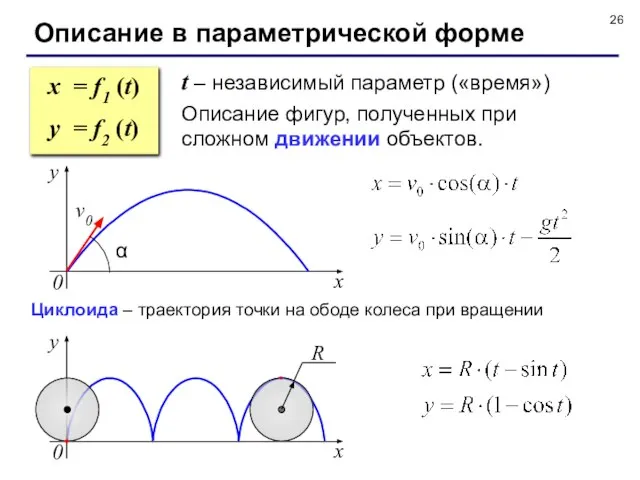
- 26. Описание в параметрической форме t – независимый параметр («время») Описание фигур, полученных при сложном движении объектов.
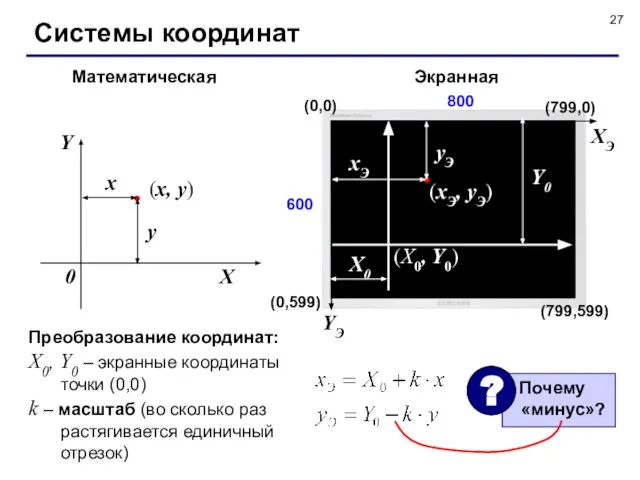
- 27. Системы координат Математическая Экранная Преобразование координат: X0, Y0 – экранные координаты точки (0,0) k – масштаб
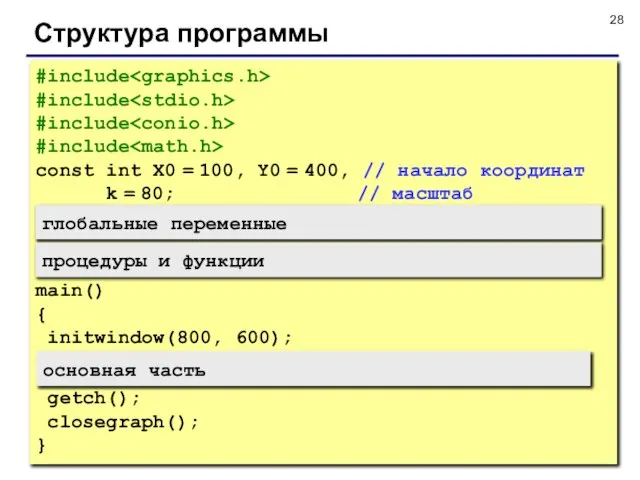
- 28. Структура программы #include #include #include #include const int X0 = 100, Y0 = 400, // начало
- 29. Перевод в экранные координаты //----------------------------------------- // SCREENX – перевод X в координаты экрана //----------------------------------------- int ScreenX
- 30. Оси координат void Axes() { line ( X0, 0, X0, 599 ); line ( 0, Y0,
- 31. Разметка оси X («черточки») (xЭ, Y0−2) (xЭ, Y0+2) Число меток на [0, xmax]: длина 800 –
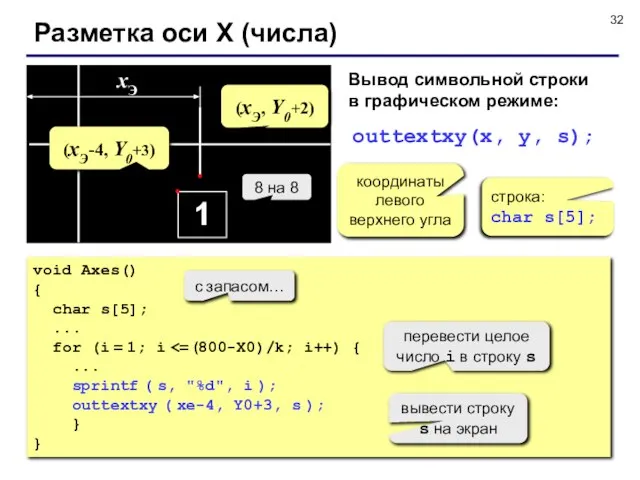
- 32. Разметка оси X (числа) 1 xЭ (xЭ, Y0+2) Вывод символьной строки в графическом режиме: outtextxy(x, y,
- 33. Оси с разметкой (полностью) void Axes() { int i, xe, ye; char s[5]; line ( X0,
- 34. Задания «4»: Сделать разметку осей полностью (не только положительной части оси X). «5»: Сделать задание на
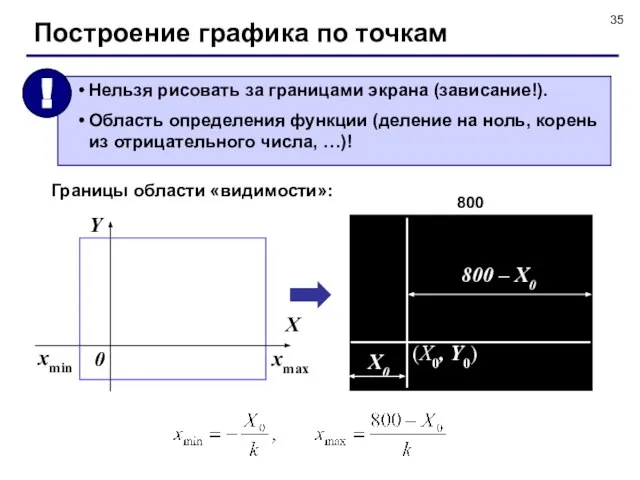
- 35. Построение графика по точкам Границы области «видимости»:
- 36. Вывод точки с проверкой //---------------------------------------- // POINT вывод пикселя с проверкой и // пересчетом координат //----------------------------------------
- 37. Описание функций //----------------------------------------- // F1, F2 // Вход: x // Выход: y = f(x) //----------------------------------------- float
- 38. Области определения //---------------------------------------- // ODZ1 – область определения f1(x) // Вход: x // Выход: 1, если
- 39. Вывод графика функции //---------------------------------------- // PLOT вывод графиков функций //---------------------------------------- void Plot () { float xmin
- 40. Общее расположение float f1 ( float x ) { return sqrt( x + 1 ); }
- 41. Задания «4»: Построить графики в соответствии с заданием. «5»: Построить графики, соединив точки линиями.
- 42. Структурное программирование на языке Си Тема 4. Точки пересечения © К.Ю. Поляков, 2007-2009
- 43. Точки пересечения f1 (x*) = f2 (x*) a b f1 (x*) – f2 (x*) = 0
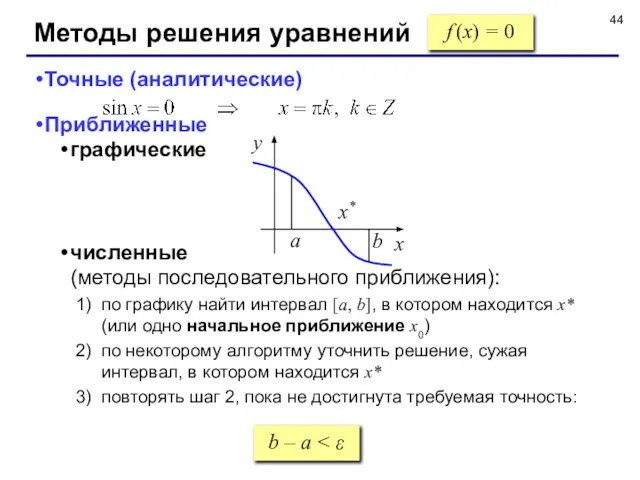
- 44. Методы решения уравнений f (x) = 0 Точные (аналитические) Приближенные графические численные (методы последовательного приближения): по
- 45. Численные методы Применение: используются тогда, когда точное (аналитическое) решение неизвестно или очень трудоемко. дают хотя бы
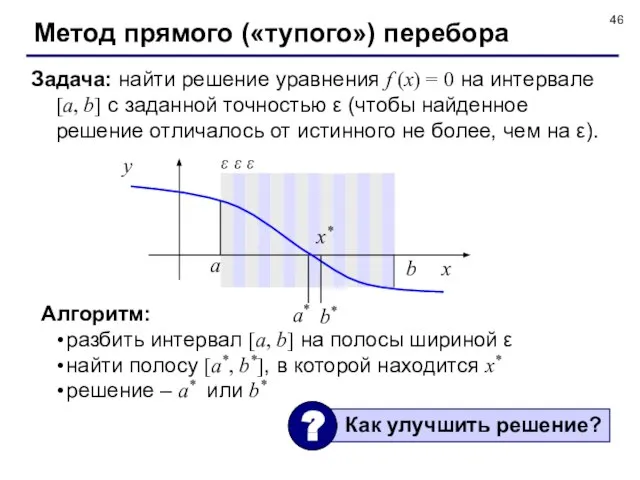
- 46. Метод прямого («тупого») перебора Задача: найти решение уравнения f (x) = 0 на интервале [a, b]
- 47. Есть ли решение на [a, b]? есть решение нет решения нет решения
- 48. Метод дихотомии (деление пополам) Найти середину отрезка [a,b]: c = (a + b) / 2; Если
- 49. Метод дихотомии (деления пополам) простота можно получить решение с любой заданной точностью нужно знать интервал [a,
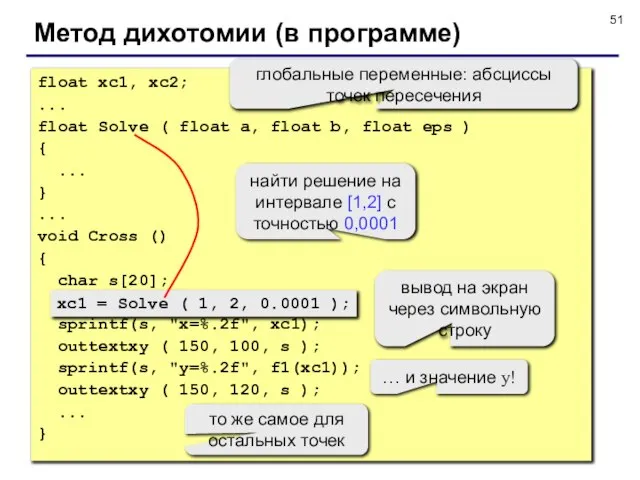
- 50. Метод дихотомии (в программе) //---------------------------------------------- // Solve находит точку пересечения на [a,b] // Вход: a, b
- 51. Метод дихотомии (в программе) float xc1, xc2; ... float Solve ( float a, float b, float
- 52. Структурное программирование на языке Си Тема 5. Штриховка © К.Ю. Поляков, 2007-2009
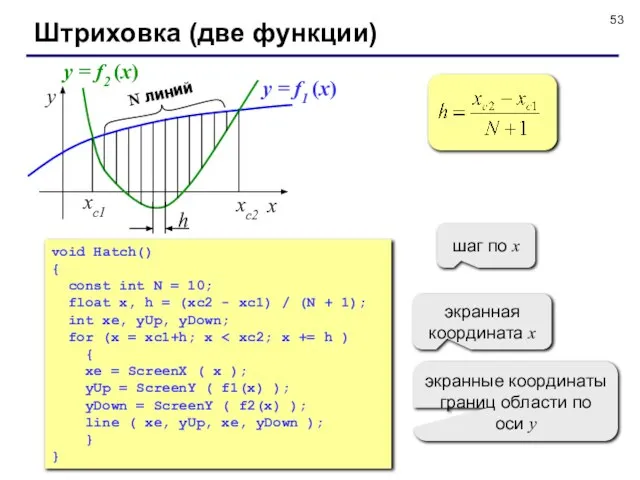
- 53. Штриховка (две функции) x y xс2 xс1 y = f1 (x) y = f2 (x) void
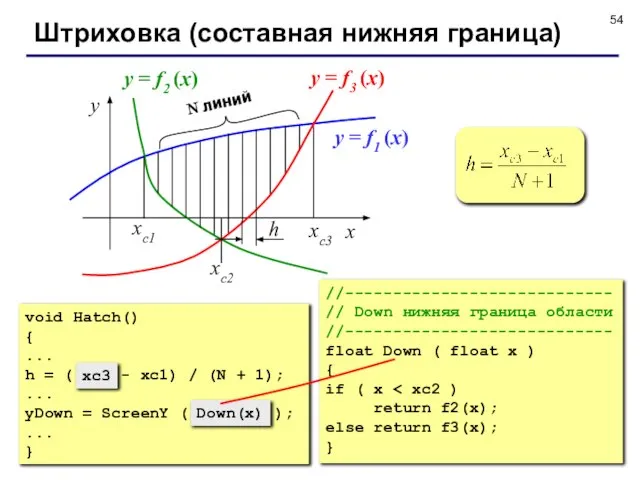
- 54. Штриховка (составная нижняя граница) x y xс3 xс1 xс2 N линий y = f1 (x) y
- 55. Штриховка (общий случай) float Up ( float x ) { ... } float Down ( float
- 56. Структурное программирование на языке Си Тема 6. Вычисление площади © К.Ю. Поляков, 2007-2009
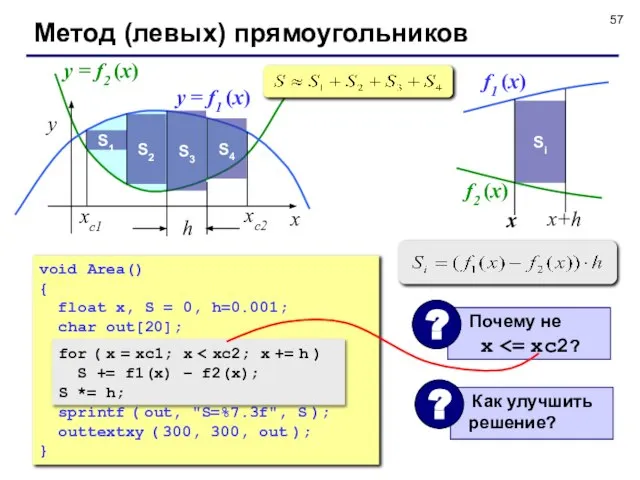
- 57. Метод (левых) прямоугольников y = f1 (x) y = f2 (x) S1 S2 S3 S4 void
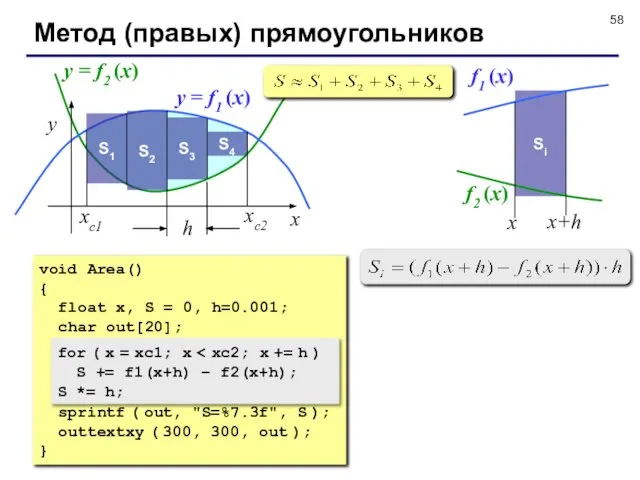
- 58. Метод (правых) прямоугольников x y xс2 xс1 y = f1 (x) y = f2 (x) S1
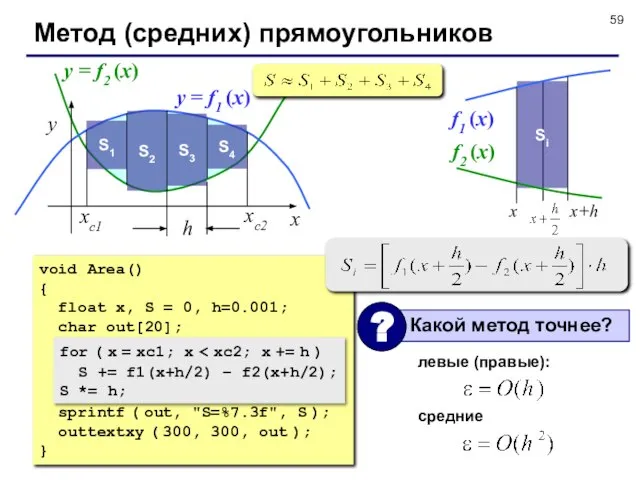
- 59. Метод (средних) прямоугольников x y xс2 xс1 y = f1 (x) y = f2 (x) S1
- 60. Метод трапеций x y xс2 xс1 y = f1 (x) y = f2 (x) for (
- 61. Метод Монте-Карло Применение: вычисление площадей сложных фигур (трудно применить другие методы). Требования: необходимо уметь достаточно просто
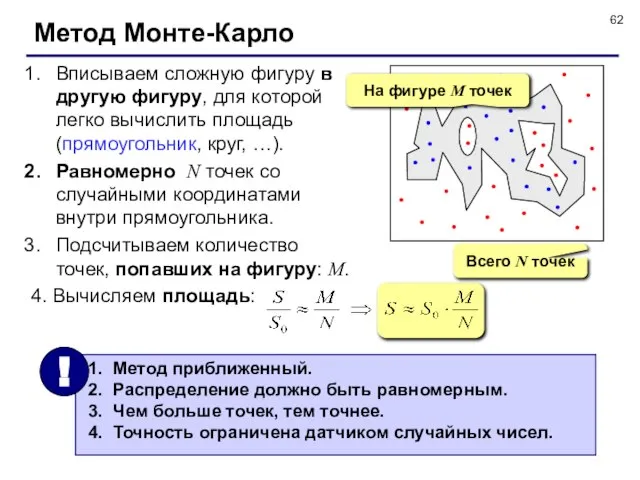
- 62. Метод Монте-Карло Вписываем сложную фигуру в другую фигуру, для которой легко вычислить площадь (прямоугольник, круг, …).
- 63. Случайное число в заданном интервале //----------------------------------------- // randF – случайное вещественное число // в заданном интервале
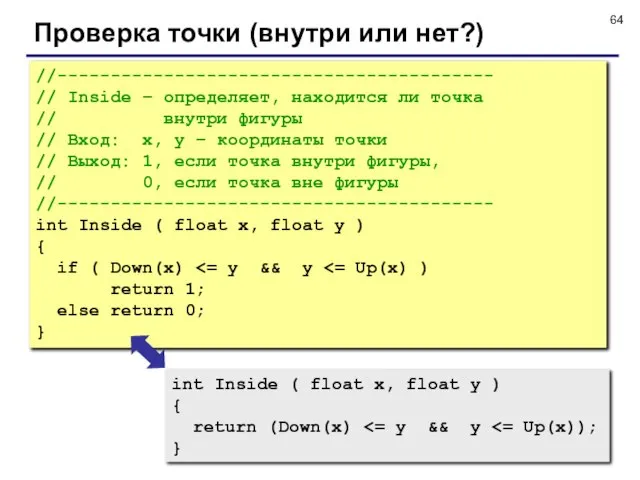
- 64. Проверка точки (внутри или нет?) //----------------------------------------- // Inside – определяет, находится ли точка // внутри фигуры
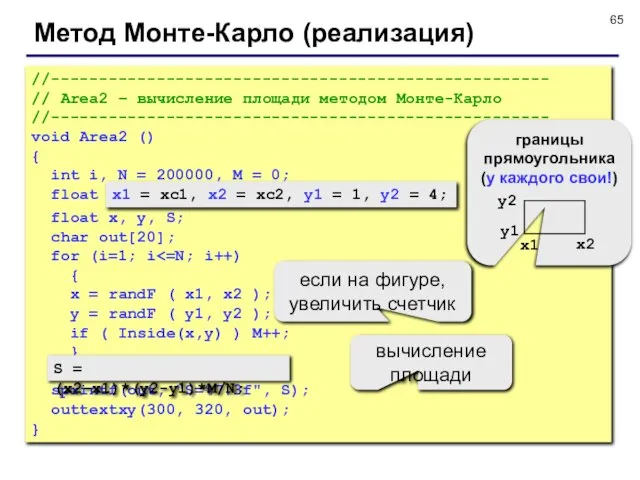
- 65. Метод Монте-Карло (реализация) //---------------------------------------------------- // Area2 – вычисление площади методом Монте-Карло //---------------------------------------------------- void Area2 () {
- 66. Структурное программирование на языке Си Тема 7. Оформление отчета © К.Ю. Поляков, 2007-2009
- 67. Титульный лист
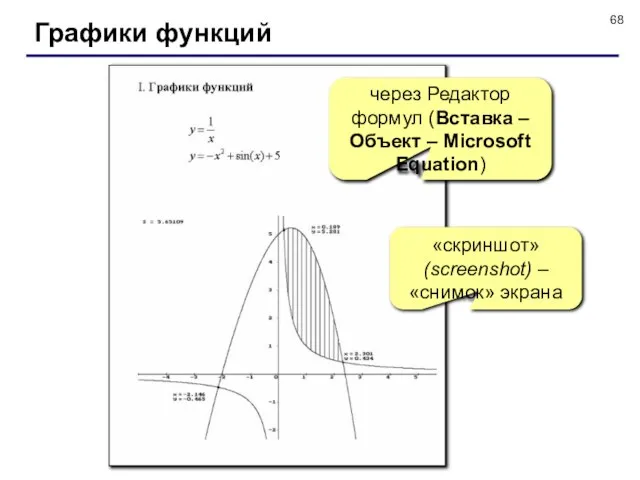
- 68. Графики функций «скриншот» (screenshot) – «снимок» экрана через Редактор формул (Вставка – Объект – Microsoft Equation)
- 69. Как получить копию экрана? Поменять цвета так, чтобы все линии и текст были белые. Запустить программу
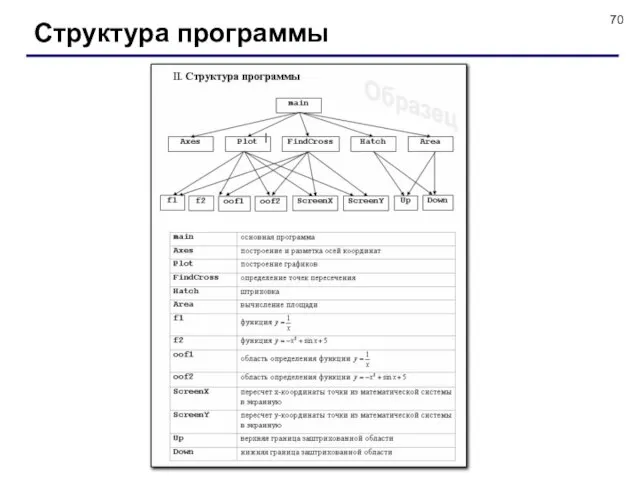
- 70. Структура программы
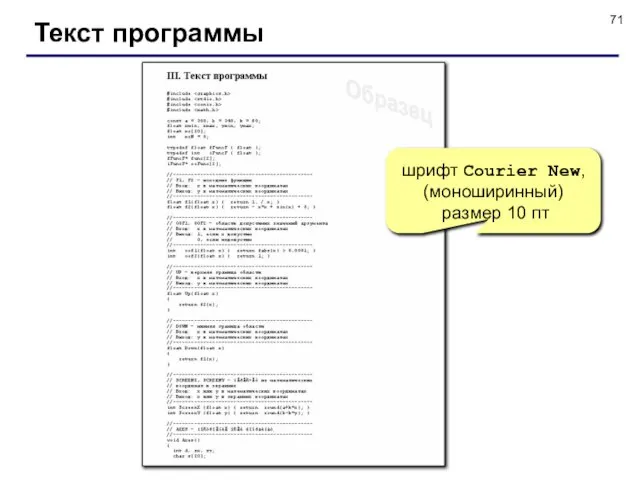
- 71. Текст программы шрифт Courier New, (моноширинный) размер 10 пт
- 73. Скачать презентацию






























![Есть ли решение на [a, b]? есть решение нет решения нет решения](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/282382/slide-46.jpg)
![Метод дихотомии (деление пополам) Найти середину отрезка [a,b]: c = (a +](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/282382/slide-47.jpg)

![Метод дихотомии (в программе) //---------------------------------------------- // Solve находит точку пересечения на [a,b]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/282382/slide-49.jpg)









 Анимированные ребусы
Анимированные ребусы Методы математического описания линейных непрерывных САУ
Методы математического описания линейных непрерывных САУ Инструктаж по прохождению программы Основы здорового питания на платформе ФБУН Новосибирский НИИ гигиены Роспотребнадзора
Инструктаж по прохождению программы Основы здорового питания на платформе ФБУН Новосибирский НИИ гигиены Роспотребнадзора Интеллектуальный анализ данных (Data Mining)
Интеллектуальный анализ данных (Data Mining) SE Ranking – комплекс незаменимых инструментов для SEO и онлайн-маркетинга
SE Ranking – комплекс незаменимых инструментов для SEO и онлайн-маркетинга Создание таблиц баз данных. Задание
Создание таблиц баз данных. Задание Наша группа
Наша группа Человек и информация
Человек и информация Установка и управление файлами на рабочих станциях и сервере
Установка и управление файлами на рабочих станциях и сервере Сертификация программных продуктов
Сертификация программных продуктов Конфигурация 1С. Почта Донбасса
Конфигурация 1С. Почта Донбасса Утилиты Windows
Утилиты Windows Интернет-эквайринг
Интернет-эквайринг Концепция развития сервисного обслуживания предприятий Машиностроительного комплекса
Концепция развития сервисного обслуживания предприятий Машиностроительного комплекса Современные интернет-коммуникации - соцсети
Современные интернет-коммуникации - соцсети Админ.воронка основные статусы
Админ.воронка основные статусы 1С:Розница 8.Аптека
1С:Розница 8.Аптека Оценка качества программного обеспечения (SQuaRE). Модели качества систем и программных продуктов ГОСТ Р ИСО/МЭК 25010–2015
Оценка качества программного обеспечения (SQuaRE). Модели качества систем и программных продуктов ГОСТ Р ИСО/МЭК 25010–2015 Алгоритмы
Алгоритмы Самый надёжный пароль. Правила составления
Самый надёжный пароль. Правила составления Вирусы. Хакеры
Вирусы. Хакеры Структура алгоритмов. Тест
Структура алгоритмов. Тест Правила поведения. Техника безопасности в кабинете информатики. Ученицы 9 «А» класса гимназии №16 г.Мытищи Чагиной Марины
Правила поведения. Техника безопасности в кабинете информатики. Ученицы 9 «А» класса гимназии №16 г.Мытищи Чагиной Марины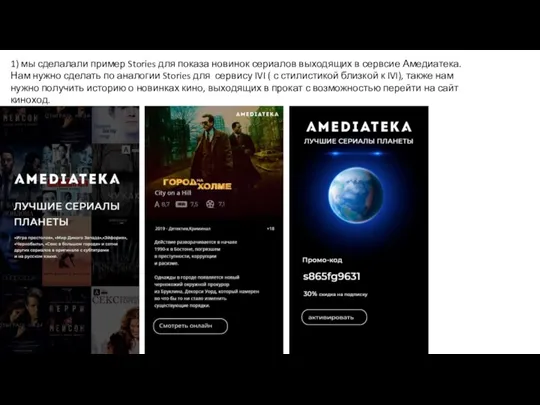 Пример Stories для показа новинок сериалов выходящих в сервисе Амедиатека
Пример Stories для показа новинок сериалов выходящих в сервисе Амедиатека С++ тілінде бағдарламалау
С++ тілінде бағдарламалау Шаблон презентации
Шаблон презентации Алгоритмическая конструкция. Повторение. Основные алгоритмические конструкции
Алгоритмическая конструкция. Повторение. Основные алгоритмические конструкции Поисковые серверы
Поисковые серверы