Содержание
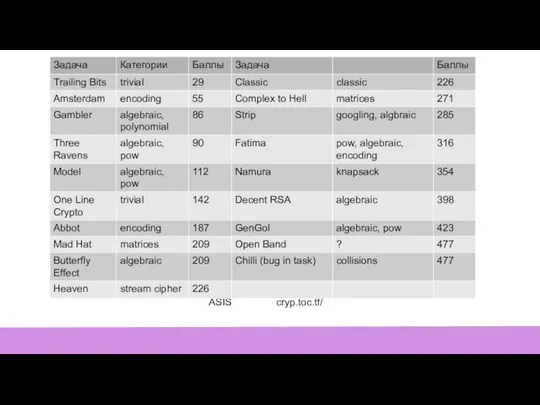
- 2. ASIS cryp.toc.tf/
- 3. Модульная арифметика Простое число - натуральное число, имеющее ровно два различных натуральных делителя — единицу и
- 4. Encoding
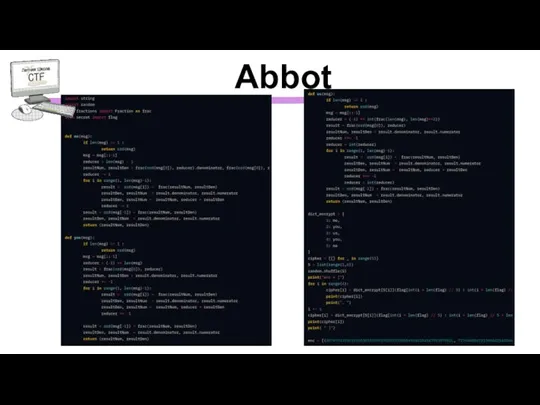
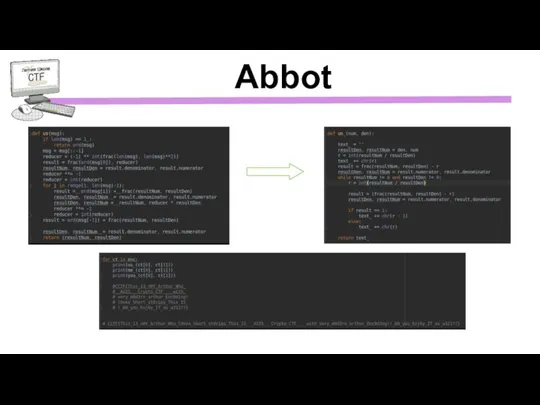
- 5. Abbot
- 6. Abbot
- 7. Amsterdam
- 8. Amsterdam
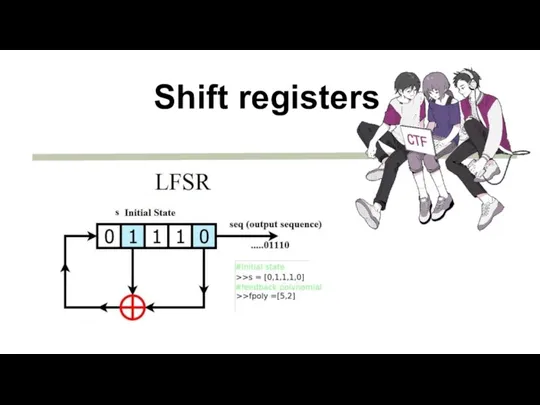
- 9. Shift registers
- 10. Heaven
- 11. Heaven
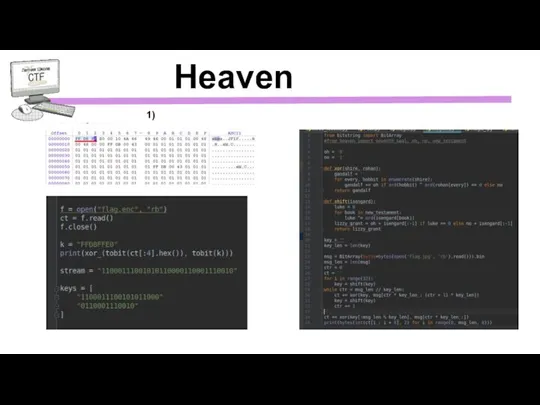
- 12. Heaven 1)
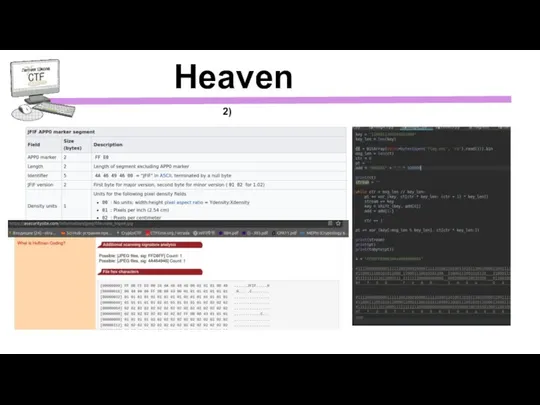
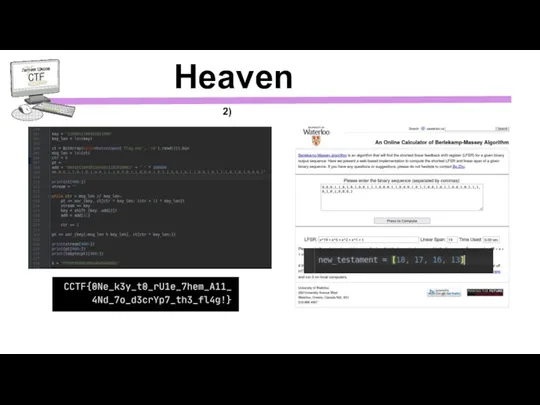
- 13. Heaven 2)
- 14. Heaven 2)
- 15. Knapsack
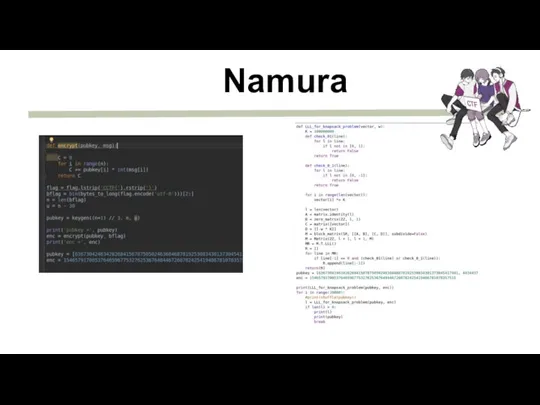
- 16. Namura
- 17. Namura
- 18. Namura
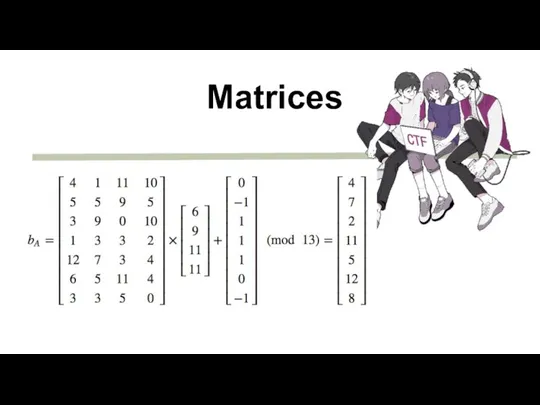
- 19. Matrices
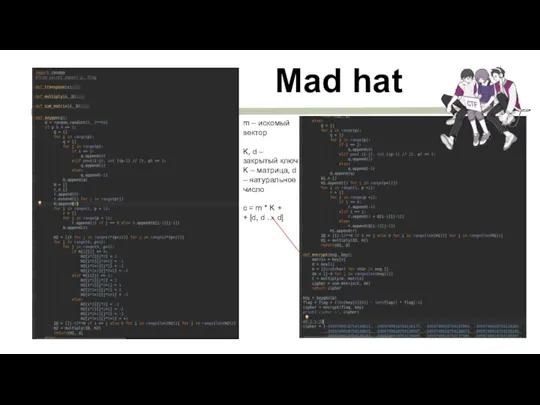
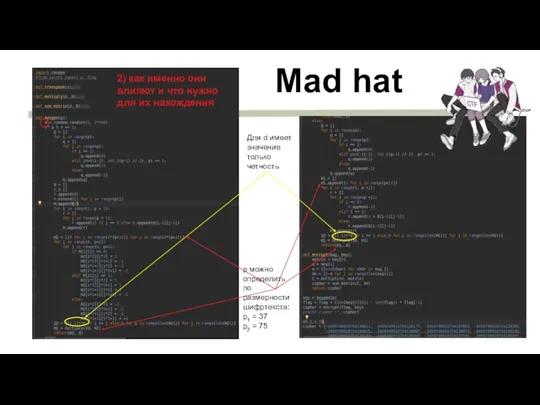
- 20. Mad hat m – искомый вектор K, d – закрытый ключ K – матрица, d –
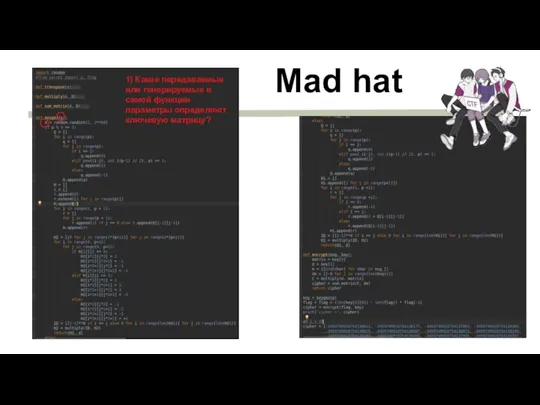
- 21. Mad hat 1) Какие передаваемые или генерируемые в самой функции параметры определяют ключевую матрицу?
- 22. Mad hat 2) как именно они влияют и что нужно для их нахождения p можно определить
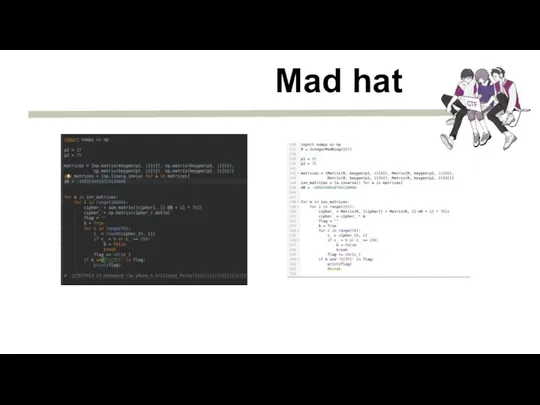
- 23. Mad hat
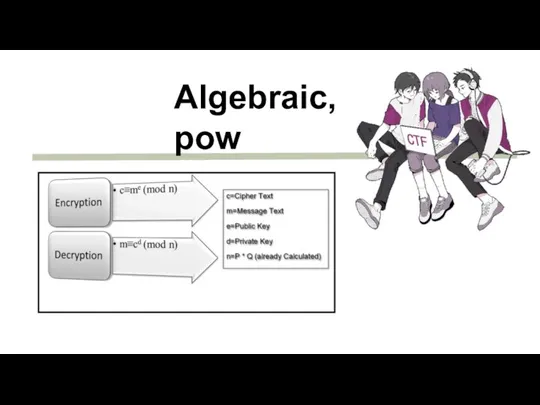
- 24. Algebraic
- 25. Gambling nc 05.cr.yp.toc.tf 33371 p, a, b – не известны f(x) ≡ x3 + ax +
- 26. Gambling nc 05.cr.yp.toc.tf 33371 p, a, b – не известны f(x) ≡ x3 + ax +
- 27. Algebraic, pow
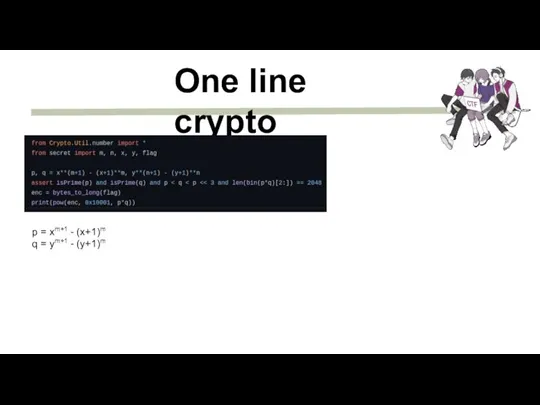
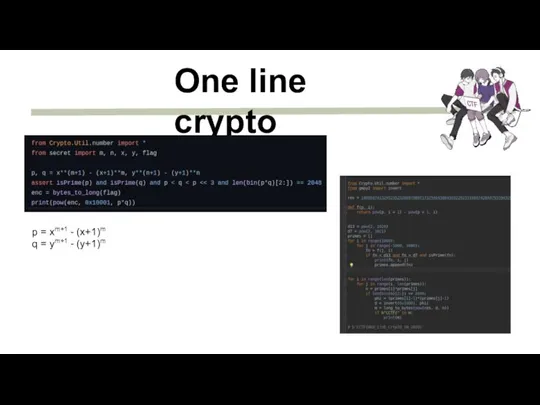
- 28. One line crypto p = xm+1 - (x+1)m q = ym+1 - (y+1)m
- 29. One line crypto p = xm+1 - (x+1)m q = ym+1 - (y+1)m
- 30. Three ravens p, q, r – простые (секретный ключ, не известны) s = p + q
- 31. Three ravens Короткое сообщение ( Известен один из множителей n c ≡ me % p*q*r*s c_
- 32. Model nc 04.cr.yp.toc.tf 8001 p, q – простые P = (q-1) // 2 Q = (p-1)
- 33. Model nc 04.cr.yp.toc.tf 8001 p, q – простые P = (q-1) // 2 Q = (p-1)
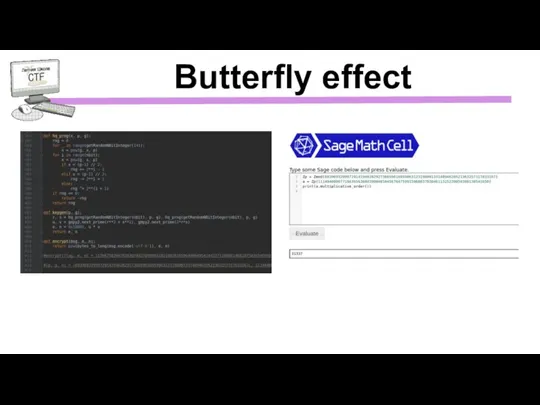
- 34. Butterfly effect
- 35. Butterfly effect
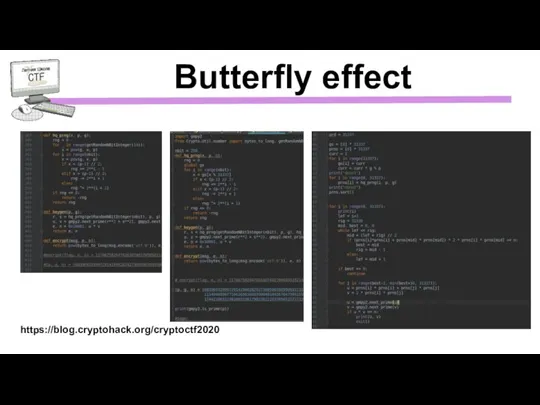
- 36. Butterfly effect https://blog.cryptohack.org/cryptoctf2020
- 37. Decent RSA -----BEGIN PUBLIC KEY----- MIIBIjANBgkqhkiG9w0BAQEFAAOCAQ8AMIIBCgKCAQEA/Ug8rlEPci1UXMsT+UDo y8DfxbTHX/3BK2oU+FPWiJf+EiUBM2x4ep04qZ1SO9Pmqj/WH9skMrF1J/LXuY3l fjvJCh0DXa9VUyX2dAJidja9Ior7GpFwwjYdKh+OETNV+2/CcX4RiPvj+8ApmedW gn4Fxaeivki+f/UwDa+ws1fTUzmI325v8yvcryHhbgeUWiF85EP6HFAavTsVPlxb LikVMAB1fuzDbqqJvW2u138w6b2FH3WrezYF6tbAyZej2HX46phwDm9C7MXYJ/sU oS+E8P7S1jMTCWjfwMCOKU3SFGrkWtXuTaoMZ2nZ+HVfJV8xJOjWez1OxQ5P3F1w GQIDAQAB -----END PUBLIC KEY-----
- 38. Decent RSA Official writeups -----BEGIN PUBLIC KEY----- MIIBIjANBgkqhkiG9w0BAQEFAAOCAQ8AMIIBCgKCAQEA/Ug8rlEPci1UXMsT+UDo y8DfxbTHX/3BK2oU+FPWiJf+EiUBM2x4ep04qZ1SO9Pmqj/WH9skMrF1J/LXuY3l fjvJCh0DXa9VUyX2dAJidja9Ior7GpFwwjYdKh+OETNV+2/CcX4RiPvj+8ApmedW gn4Fxaeivki+f/UwDa+ws1fTUzmI325v8yvcryHhbgeUWiF85EP6HFAavTsVPlxb LikVMAB1fuzDbqqJvW2u138w6b2FH3WrezYF6tbAyZej2HX46phwDm9C7MXYJ/sU oS+E8P7S1jMTCWjfwMCOKU3SFGrkWtXuTaoMZ2nZ+HVfJV8xJOjWez1OxQ5P3F1w GQIDAQAB -----END PUBLIC
- 40. Скачать презентацию


















 Zakony_logiki_Ravnosilnye_preobrazovania
Zakony_logiki_Ravnosilnye_preobrazovania Платформа Freescale Semiconductor для реализации беспроводных решений ZigBee / 802.15.4 / SMAC
Платформа Freescale Semiconductor для реализации беспроводных решений ZigBee / 802.15.4 / SMAC Кодирование информации
Кодирование информации Маркетинговые особенности контента социальных сетей. Лекция № 6
Маркетинговые особенности контента социальных сетей. Лекция № 6 Планирование структуры локальной сети и подключение устройств
Планирование структуры локальной сети и подключение устройств Installation testing mentoring program for manual QA
Installation testing mentoring program for manual QA Алгоритмы линейного поиска
Алгоритмы линейного поиска Взаимодействия прикладной программы и программы с потенциально опасными последствиями
Взаимодействия прикладной программы и программы с потенциально опасными последствиями Информационная безопасность
Информационная безопасность Системы счисления: продолжение
Системы счисления: продолжение Цифровая платформа Van & Gog. Цифровая платформаприложение
Цифровая платформа Van & Gog. Цифровая платформаприложение Синий экран смерти BSoD
Синий экран смерти BSoD Программное обеспечение (caffein)
Программное обеспечение (caffein) История цифровой вычислительной техники
История цифровой вычислительной техники Лекция 6_информатика_ЭТ
Лекция 6_информатика_ЭТ BlockChain
BlockChain Интегрируем 1С и 1С-bitrix
Интегрируем 1С и 1С-bitrix Блог как форма личного и корпоративного Интернет-представительства педагогических работников
Блог как форма личного и корпоративного Интернет-представительства педагогических работников SQL. Вложенные запросы. Правила создания запросов
SQL. Вложенные запросы. Правила создания запросов Агрегирование каналов
Агрегирование каналов Сфера деятельности: графический дизайн, веб-дизайн
Сфера деятельности: графический дизайн, веб-дизайн Opening the windows just fly! (Открывая окна – летайте!)
Opening the windows just fly! (Открывая окна – летайте!) Какую рекламу запускать в первую очередь в интернете
Какую рекламу запускать в первую очередь в интернете Инструкция по установке программного обеспечения ArTecрвом веке
Инструкция по установке программного обеспечения ArTecрвом веке Национальные проекты цифровизации российской экономики
Национальные проекты цифровизации российской экономики RPC в NodeJS
RPC в NodeJS 1__NodeJS._NodeJS
1__NodeJS._NodeJS Операционные системы, среды и оболочки. Файловая система. Физическая организация
Операционные системы, среды и оболочки. Файловая система. Физическая организация