Разбор задач ЕГЭ. Кодирование чисел. Системы счисления. В7

Задача 1.
ИНФОРМАТИКА
2014г. Кирсанов Илья Андреевич ©
В системе счисления с некоторым основанием десятичное число 18 записывается в виде 30. Укажите это основание.
Решение.
Пусть x – неизвестное основание системы, тогда справедливо равенство:
3*x1+0*x0=18;
3*x=18;
x=6, основание системы 6.
Ответ 6

N
Задача 1.
ИНФОРМАТИКА
2014г. Кирсанов Илья Андреевич ©
Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 71 оканчивается на 13.
Решение.
Минимально возможная система счисления – 4, т.к. у нас есть цифра 3.
Пусть основание искомой системы = X, тогда
X2*c+1*X1+3*X0=71, где с – натуральное число либо 0.
Зная что X0=1,X1=X, получим X2*c+X+3=71.
Отсюда
Чем больше X, тем меньше с, поэтому значения с не превышают (68-4)/(4*4)=4. Переменная с [0..4]

N
Задача 1.
ИНФОРМАТИКА
2014г. Кирсанов Илья Андреевич ©
Получаем:
а) при c=0, X=68.
б)при c=1,2,3 решения — не целые числа;
в) при c =4, X1=4 и X2=-4.25 условию натуральности соответствует только первое решение.
Ответ 4,68

Задача 2.
ИНФОРМАТИКА
2014г. Кирсанов Илья Андреевич ©
Укажите, сколько всего раз встречается цифра 2 в записи чисел 10, 11, 12, …, 17 в системе счисления с основанием 5.
Решение.
Переведем числа 10 и 17(первое и последнее) в систему с основанием пять:
1010=205, 1010=325, затем выпишем все числа, находящиеся между этими двумя и содержащие двойку:
205, 215, 225, 235, 245, 325 – всего 7 двоек.
Ответ 7

Задача 3.
ИНФОРМАТИКА
2014г. Кирсанов Илья Андреевич ©
Запись числа 180 в системе счисления с основанием N содержит 3 цифры и оканчивается на 0. Перечислите в порядке возрастания все возможные основания системы счисления.
Решение.
N2*x+N1*y+0*N0=180
N*(N*x+y)=180
Максимальное N достигается при x=1, y=0,т.е. N max = 13.
Почему x не равен 0? Ответ прост, тогда бы мы имели двузначное число, а это противоречит условию.
Почему N max = 13? Потому что мы выбираем ближайшее целое значение < либо = корню 180.
Так как последняя цифра 0, выходит что 180 разделилось на основание системы нацело и в остатке вышел 0. Следовательно основание системы – делитель числа 180 и этот делитель не превышает 13. Делители: 2,3,4,5,6,9,10,12

Задача 3.
ИНФОРМАТИКА
2014г. Кирсанов Илья Андреевич ©
Не все делители подойдут. Можно проверить их подстановкой, окажется, что подойдут только 6,9,10,12.
Ответ 6,9,10,12

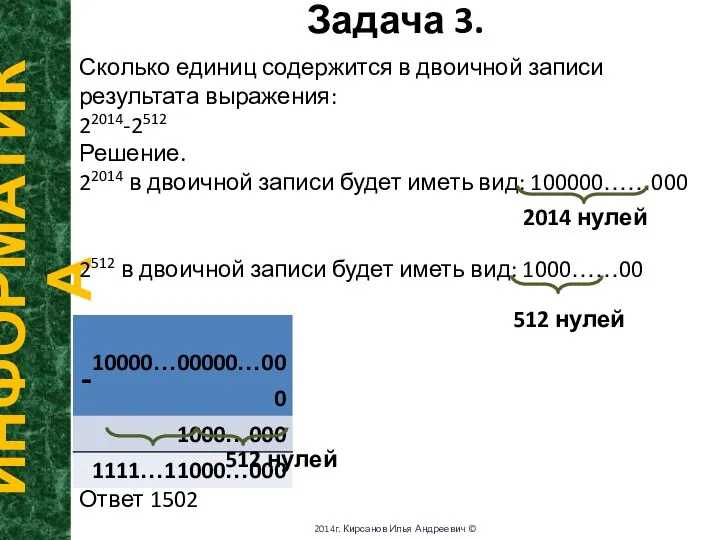
Задача 3.
ИНФОРМАТИКА
2014г. Кирсанов Илья Андреевич ©
Сколько единиц содержится в двоичной записи результата выражения:
22014-2512
Решение.
22014 в двоичной записи будет иметь вид: 100000……000
2512 в двоичной записи будет иметь вид: 1000……00
Ответ 1502
2014 нулей
1502 единицы
512 нулей
512 нулей

Вопросы.
ИНФОРМАТИКА
2014г. Кирсанов Илья Андреевич ©
Запись числа 23 в некоторой системе счисления выглядит так:212q Найдите основание системы счисления q.
Ответ 3

Вопросы.
ИНФОРМАТИКА
2014г. Кирсанов Илья Андреевич ©
Укажите наименьшее основание системы счисления, в которой запись числа 70 трехзначна.
Ответ 5

Вопросы.
ИНФОРМАТИКА
2014г. Кирсанов Илья Андреевич ©
Найдите основание системы счисления, в которой выполнено сложение: 144 + 24 = 201.
Ответ 7

Вопросы.
ИНФОРМАТИКА
2014г. Кирсанов Илья Андреевич ©
Запись числа 338 в системе счисления с основанием N содержит 3 цифры и оканчивается на 2. Чему равно максимально возможное основание системы счисления?
Ответ 16

Вопросы.
ИНФОРМАТИКА
2014г. Кирсанов Илья Андреевич ©
Укажите через запятую в порядке возрастания все десятичные числа, не превосходящие 25, запись которых в двоичной системе счисления оканчивается на 101?
Ответ 5,13,21

Вопросы.
ИНФОРМАТИКА
2014г. Кирсанов Илья Андреевич ©
Укажите через запятую в порядке возрастания все десятичные числа, не превосходящие 30, запись которых в системе счисления с основанием 5 начинается на 3?
Ответ 3,15,16,17,18,19

Вопросы.
ИНФОРМАТИКА
2014г. Кирсанов Илья Андреевич ©
Решите уравнение: 1007 + x = 2105.Ответ запишите в шестеричной системе (основание системы счисления в ответе писать не нужно).
Ответ 10

Вопросы.
ИНФОРМАТИКА
2014г. Кирсанов Илья Андреевич ©
Сколько единиц содержится в двоичной записи результата выражения:
(32*1016)333-22012-4999
Ответ 986