Слайд 2Элементы теории множеств
Понятие множества является неопределяемым понятием.
Множество не обладает внутренней

структурой.
Множество можно представить себе как совокупность элементов, обладающих некоторым общим свойством.
Слайд 3Операции над множествами
Основными операциями над множествами являются
объединение,
пересечение
разность.

Слайд 4Объединение
Определение 1. Объединением двух множеств называется новое множество

Слайд 5Пересечением
Определение 2. Пересечение двух множеств называется новое множество

Слайд 6Разность
Определение 3. Разностью двух множеств называется новое множество

Слайд 7Декартово произведение множеств

Слайд 8Отношение
Определение 6. Подмножество R декартового произведения множеств
называется отношением степени n

(n-арным отношением).
Слайд 10Типы данных, используемые в реляционной модели
Для реляционной модели данных тип используемых

данных не важен.
Требование, чтобы тип данных был простым, нужно понимать так, что в реляционных операциях не должна учитываться внутренняя структура данных.
Слайд 11Домен
Домен можно рассматривать как подмножество значений некоторого типа данных имеющих определенный смысл.

Домен характеризуется следующими свойствами:
Домен имеет уникальное имя (в пределах базы данных).
Домен определен на некотором простом типе данных или на другом домене.
Домен может иметь некоторое логическое условие, позволяющее описать подмножество данных, допустимых для данного домена.
Домен несет определенную смысловую нагрузку.
Слайд 12Отношение
Определение 1. Атрибут отношения есть пара вида
<Имя_атрибута : Имя_домена>.
Имена атрибутов

должны быть уникальны в пределах отношения. Часто имена атрибутов отношения совпадают с именами соответствующих доменов.
Определение 2. Отношение , определенное на множестве доменов (не обязательно различных), содержит две части: заголовок и тело.
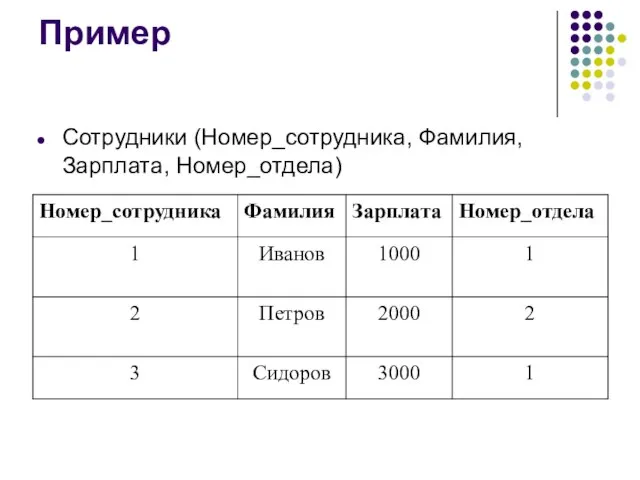
Слайд 14Пример
Сотрудники (Номер_сотрудника, Фамилия, Зарплата, Номер_отдела)
Слайд 15Отношения, совместимые по типу
Определение Будем называть отношения совместимыми по типу, если они

имеют идентичные заголовки, а именно,
Отношения имеют одно и то же множество имен атрибутов, т.е. для любого атрибута в одном отношении найдется атрибут с таким же наименованием в другом отношении,
Атрибуты с одинаковыми именами определены на одних и тех же доменах.
Слайд 16Теоретико-множественные операторы
Объединение
Пересечение
Вычитание
Декартово произведение

Слайд 17Объединение
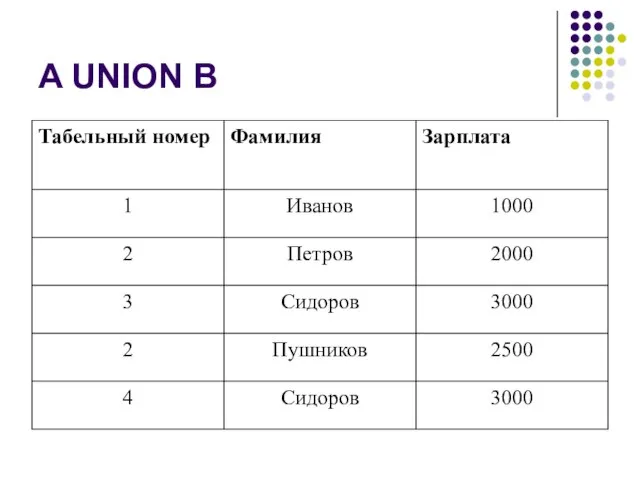
Определение 2. Объединением двух совместимых по типу отношений A и B называется

отношение с тем же заголовком, что и у отношений A и B , и телом, состоящим из кортежей, принадлежащих или A, или B, или обоим отношениям.
Синтаксис операции объединения:
A UNION B
Слайд 18Пример
Пусть даны два отношения А и В с информацией о сотрудниках:

Слайд 20Пересечение
Определение Пересечением двух совместимых по типу отношений A и B называется

отношение с тем же заголовком, что и у отношений A и B , и телом, состоящим из кортежей, принадлежащих одновременно обоим отношениям A и B .
A INTERSECT B
Слайд 21Пример
Для тех же отношений А и В , что и в предыдущем

примере пересечение имеет вид:
Слайд 22Вычитание
Определение 4. Вычитанием двух совместимых по типу отношений А и В

называется отношение с тем же заголовком, что и у отношений А и В , и телом, состоящим из кортежей, принадлежащих отношению А и не принадлежащих отношению В.
A MINUS B
Слайд 23Пример
Для тех же отношений А и В , что и в предыдущем

примере вычитание имеет вид:
Слайд 26Декартово произведение отношений

Слайд 27Специальные реляционные операторы
Выборка
Проекция
Соединение
Деление

Слайд 28Выборка (ограничение, селекция)
Определение. Выборкой (ограничением, селекцией) на отношении А с условием с

называется отношение с тем же заголовком, что и у отношения А , и телом, состоящем из кортежей, значения атрибутов которых при подстановке в условие с дают значение ИСТИНА.
с представляет собой логическое выражение, в которое могут входить атрибуты отношения и (или) скалярные выражения.
А where c
Слайд 29Пример
Результат выборки A WHERE зарплпта < 3000 будет иметь вид:

Слайд 30Проекция
Определение 7. Проекцией отношения A по атрибутам (X,Y,….Z), где каждый из атрибутов

принадлежит отношению A , называется отношение с заголовком и телом, содержащим множество кортежей вида (x,y,…z), таких, для которых в отношении A найдутся кортежи со значением атрибута X равным x, значением атрибута Y равным y, …, значением атрибута Z равным z .
A[X,y…Z]
Слайд 31Пример
Отношение
A[Город поставщика]
![Пример Отношение A[Город поставщика]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/851286/slide-30.jpg)
Слайд 32Соединение
Общая операция соединения
тэта-соединение
Экви-соединение
Естественное соединение

Слайд 33Общая операция соединения
Определение. Соединением отношений А и В по условию с называется

отношение
(A TIMES B) Where c
c представляет собой логическое выражение, в которое могут входить атрибуты отношений A и B и (или) скалярные выражения.
Слайд 34Тэта-соединение
Определение. Пусть отношение А содержит атрибут X, отношение B содержит атрибут Y,

а θ - один из операторов сравнения ( и т.д.). Тогда -соединением отношения A по атрибуту X с отношением B по атрибуту Y называют отношение
(A TIMES B) WHERE X θ Y
Слайд 35ЭКВИ-СОЕДИНЕНИЕ
Наиболее важным частным случаем θ -соединения является случай, когда есть просто равенство.
![ЭКВИ-СОЕДИНЕНИЕ Наиболее важным частным случаем θ -соединения является случай, когда есть просто равенство. A[X=Y]B](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/851286/slide-34.jpg)
A[X=Y]B
Слайд 39Естественное соединение
A JOIN B

Слайд 44Примеры
Получить имена поставщиков, поставляющих деталь номер 2.
Получить имена поставщиков, поставляющих по

крайней мере одну гайку.
Слайд 45Получить имена поставщиков, поставляющих все детали.
Получить имена поставщиков, не поставляющих деталь

номер 2.




























![Пример Отношение A[Город поставщика]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/851286/slide-30.jpg)



![ЭКВИ-СОЕДИНЕНИЕ Наиболее важным частным случаем θ -соединения является случай, когда есть просто равенство. A[X=Y]B](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/851286/slide-34.jpg)


![P[PNUM=PNUM]PD](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/851286/slide-37.jpg)







 Поместите здесь ваш текст. Шаблон
Поместите здесь ваш текст. Шаблон Построение 3D-моделей с помощью информационных систем. 3D- печать. Практическая работа №4
Построение 3D-моделей с помощью информационных систем. 3D- печать. Практическая работа №4 Поток - порядок вывода объектов на странице cверху вниз
Поток - порядок вывода объектов на странице cверху вниз Модифицированный метод шифрования
Модифицированный метод шифрования Магистрально-модульный принцип построения компьютера
Магистрально-модульный принцип построения компьютера Деревья. Обход всего дерева. (Лекция 2)
Деревья. Обход всего дерева. (Лекция 2) Информатика для 4 класса. Компьютерные программы
Информатика для 4 класса. Компьютерные программы Wish list
Wish list Возможности использования электронных энциклопедий и разработок уроков в преподавании изо и черчения
Возможности использования электронных энциклопедий и разработок уроков в преподавании изо и черчения Функции информационного менеджмента. Формирование технологической среды сферы информатизации предприятия
Функции информационного менеджмента. Формирование технологической среды сферы информатизации предприятия Передача информации. Электронная почта
Передача информации. Электронная почта Средства организации чертежа в САПР. Слои и свойства объектов
Средства организации чертежа в САПР. Слои и свойства объектов Системы счисления
Системы счисления Автор работы: учитель начальных классов МБОУ «Зензелинская СОШ» Лиманского района Астраханской области Пивоварова Анжела Анатол
Автор работы: учитель начальных классов МБОУ «Зензелинская СОШ» Лиманского района Астраханской области Пивоварова Анжела Анатол Обзор Pentaho BI
Обзор Pentaho BI Комп‘ютерний практикум № 3. Програма для обчислення числа із заданою точністю
Комп‘ютерний практикум № 3. Програма для обчислення числа із заданою точністю Использование социальных сетей в деятельности педагога
Использование социальных сетей в деятельности педагога Сберкласс
Сберкласс Microsoft Project для управления проектами
Microsoft Project для управления проектами Web-страницы. Язык HTML
Web-страницы. Язык HTML Аппаратное обеспечение. Устройства хранения информации. (Лекция 4)
Аппаратное обеспечение. Устройства хранения информации. (Лекция 4) Google. Топ фактів
Google. Топ фактів Разработка мер по защите информации в АСУ АСУ – навигация Алтайский край
Разработка мер по защите информации в АСУ АСУ – навигация Алтайский край Изучение возможностей и синтаксиса Python: Строки и работа с файлами. 7 занятие
Изучение возможностей и синтаксиса Python: Строки и работа с файлами. 7 занятие Информационные технологии в дизайне
Информационные технологии в дизайне Логические операции в Excel
Логические операции в Excel Сайт. Запчасти для двигателей САТ
Сайт. Запчасти для двигателей САТ Передача информации
Передача информации