Содержание
- 2. Алгебра логики — это математический аппарат, с помощью которого записывают, вычисляют, упрощают и преобразовывают логические высказывания.
- 3. В алгебре логики высказывания обозначают буквами и называют логическими переменными. Если высказывание истинно, то значение соответствующей
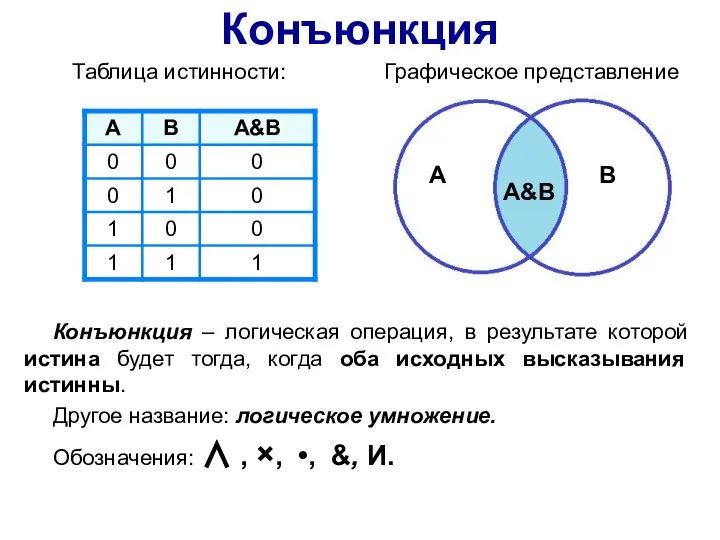
- 4. Таблица истинности: Графическое представление A B А&В Конъюнкция Конъюнкция – логическая операция, в результате которой истина
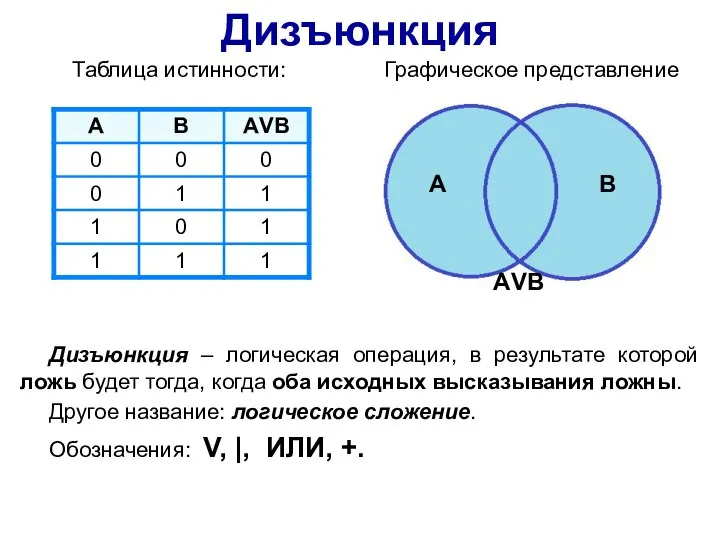
- 5. Таблица истинности: Графическое представление A B АVВ Дизъюнкция Дизъюнкция – логическая операция, в результате которой ложь
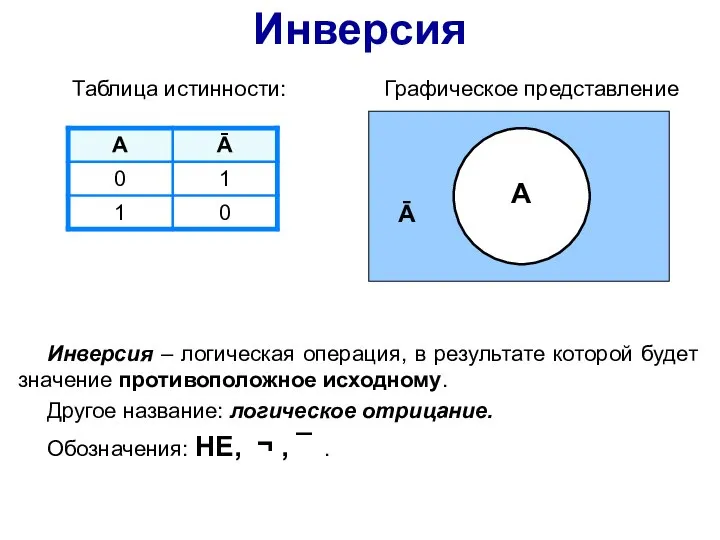
- 6. Таблица истинности: Графическое представление A Ā Инверсия Инверсия – логическая операция, в результате которой будет значение
- 7. Таблица истинности: Импликация Импликация – логическая операция, в результате которой истина будет тогда, когда первое высказывание
- 8. Таблица истинности: Эквивалентность Импликация – логическая операция, в результате которой истина будет тогда, когда оба высказывания
- 9. Логические выражения При вычислении логических выражений сначала выполняются действия в скобках. Приоритет выполнения логических операций: ¬,
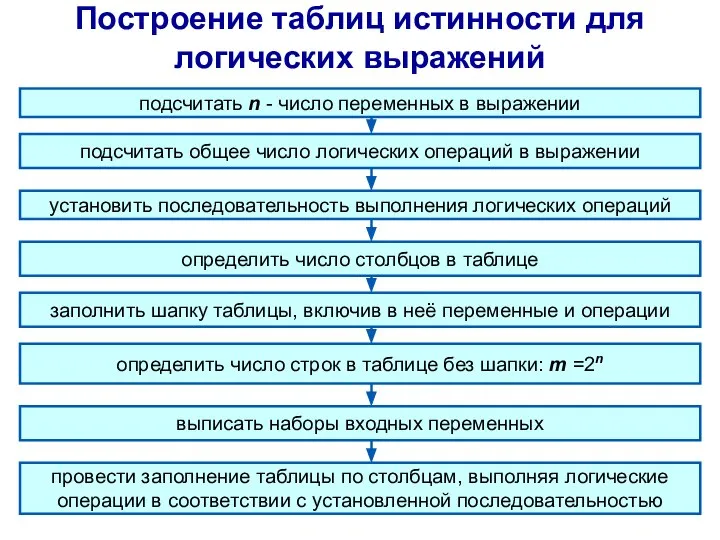
- 10. Построение таблиц истинности для логических выражений подсчитать n - число переменных в выражении подсчитать общее число
- 11. Построить таблицу истинности для выражения А V A & B Число переменных: N = 2 Число
- 12. Переместительный (коммутативный) закон Для логического сложения: Для логического умножения:
- 13. Сочетательный (ассоциативный) закон Для логического сложения: Для логического умножения: При одинаковых знаках скобки можно ставить произвольно
- 14. Распределительный (дистрибутивный) закон Для логического сложения: Для логического умножения:
- 15. Закон двойного отрицания Двойное отрицание исключает отрицание
- 16. Закон исключения третьего Из двух противоречащих высказываний об одном и том же предмете одно всегда истинно,
- 17. Закон противоречия Невозможно, чтобы противоречащие высказывания были одновременно истинными.
- 18. Закон повторения (равносильности) Для логического сложения: Для логического умножения: Закон означает отсутствие показателей степени
- 19. Закон исключения констант Для логического сложения: Для логического умножения:
- 20. Закон общей инверсии ( законы де Моргана) Для логического сложения: Для логического умножения:
- 21. Упражнения (самоконтроль) Постройте таблицы истинности для следующих логических выражений: 1) B v B & A 2)
- 23. Скачать презентацию
















 Приборные интерфейсы; назначение и организация
Приборные интерфейсы; назначение и организация Разработка прототипа автоматизированной системы сбора, классификации и реферирования публикаций СМИ из новостных источников
Разработка прототипа автоматизированной системы сбора, классификации и реферирования публикаций СМИ из новостных источников Сайты Лекция 6.10
Сайты Лекция 6.10 Приложение для сортировки аудиофайлов
Приложение для сортировки аудиофайлов Операционная система
Операционная система Лекция 8.Бинарный поиск элемента в упорядоченном линейном массиве
Лекция 8.Бинарный поиск элемента в упорядоченном линейном массиве Key elements of the control system
Key elements of the control system Информационные коммуникации и эффективность управления в малом бизнесе
Информационные коммуникации и эффективность управления в малом бизнесе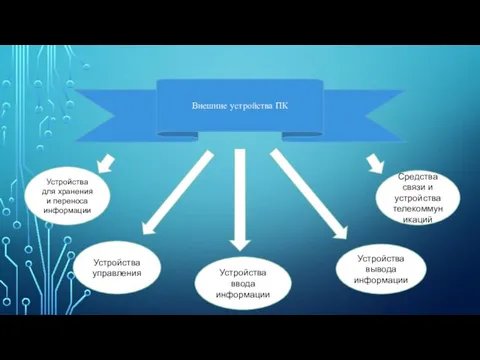 Внешние устройства ПК
Внешние устройства ПК Программирование на языке Pascal
Программирование на языке Pascal Interpreters' note-taking (INT). Универсальная переводческая скоропись
Interpreters' note-taking (INT). Универсальная переводческая скоропись Гиперссылки. Призентации
Гиперссылки. Призентации Базы данных (БД)
Базы данных (БД) Модель Мусса
Модель Мусса Игра на реакцию Уклонись от предмета
Игра на реакцию Уклонись от предмета Лекция_2 (1)
Лекция_2 (1) Микроядро Mach. ОС на его основе
Микроядро Mach. ОС на его основе Марафон Весенний каприз в инстаграм
Марафон Весенний каприз в инстаграм Анализ методов и средств резервного копирования
Анализ методов и средств резервного копирования 18_HTML5__
18_HTML5__ Мобильное приложенеие Simplification of studies
Мобильное приложенеие Simplification of studies Интерфейс
Интерфейс Пример презентации. Р/Д
Пример презентации. Р/Д Разработка веб-сайта для выбора автомобиля по заданным пользователем критериям
Разработка веб-сайта для выбора автомобиля по заданным пользователем критериям Циклы в С++
Циклы в С++ 171050c0d77745468ac9eed15021cb0d
171050c0d77745468ac9eed15021cb0d Мультиретаргетинг
Мультиретаргетинг Sensational clean
Sensational clean