Реляционное исчисление кортежей. Система запросов

Исчисле́ние
Лат. calculus — небольшой камешек, используемый для подсчёта.

Система запросов
«Реляционное исчисление кортежей»

Система запросов
«Реляционное исчисление кортежей»

Выражение
реляционного исчисления кортежей
x – переменная TC
f – предикат
{x(R) | f(x)} – выражение TC, если:
f(x) разрешена над TC
x – единственная переменная в f(x), имеющая свободный тип вхождения
R ⊆ U
Если type(x, f) определен, то type(x, f) = R, иначе R ⊇ men(f,x)

Выражение
реляционного исчисления кортежей
Отношение, определяемое выражением TC:
r(R) = {t(R) : f(t) ≡ true}
type(x, f) – тип переменной x в формуле f
men(f, x) – множество ссылок переменной x в формуле f

Формула
реляционного исчисления кортежей

Формула
реляционного исчисления кортежей

Формула
реляционного исчисления кортежей
II. Формула

Формула
реляционного исчисления кортежей
II. Формула
Примечание
Допускается следующий вариант записи формул:
Qx(R)∈r(f)
x – переменный кортеж,
f ∍ x – формула,
r ∈ d – отношение,
R ⊆ U,
Q – квантор

Разрешенная формула
реляционного исчисления кортежей

Разрешенная формула
реляционного исчисления кортежей
Формула
g – разрешенная формула
f = ¬g ⇨ f – разрешена
типы вхождения переменных в f, а также типы и
множества ссылок, сохраняются по сравнению
с типами вхождения переменных в g
type(x, f) = type(x, g), men(x, f) = men(x, g)

Разрешенная формула
реляционного исчисления кортежей
Формула
g, h – разрешенные формулы f = g ∧ h ⇨ f – разрешена
типы вхождения переменных в f сохраняются по
сравнению с типами вхождения переменных в g
type(x, f) = type(x, g) = type(x, h), если определены
type(x, g) и type(x, h)
type(x, f) = type(x, g), если определен type(x, g), но не
определен type(x, h); men(x, h) ⊆ type(x, g)
men(x, f) = men(x, g) ∪ men(x, h), если не определены
type(x, g) и type(x, h)

Разрешенная формула
реляционного исчисления кортежей
Формула
g, h – разрешенные формулы f = g ∨ h ⇨ f – разрешена
типы вхождения переменных в f сохраняются по
сравнению с типами вхождения переменных в g
type(x, f) = type(x, g) = type(x, h), если определены
type(x, g) и type(x, h)
type(x, f) = type(x, g), если определен type(x, g), но не
определен type(x, h); men(x, h) ⊆ type(x, g)
men(x, f) = men(x, g) ∪ men(x, h), если не определены
type(x, g) и type(x, h)

Разрешенная формула
реляционного исчисления кортежей
Формула
g – разрешенная формула
f = ∃x(R)g
f разрешена, если тип вхождения х в g – свободный,
type(x, g) = R (если type(x, g) определен в g) или
men(x, g) ⊆ R
тип вхождения х в g – связанный ⇨ type(x, f) и
men(x, f) не определены
типы вхождения переменных, ≠ х, в f сохраняются
по сравнению с типами вхождения переменных в g

Разрешенная формула
реляционного исчисления кортежей
Формула
g – разрешенная формула
f = ∀x(R)g
f разрешена, если тип вхождения х в g – свободный,
type(x, g) = R (если type(x, g) определен в g) или
men(x, g) ⊆ R
тип вхождения х в g – связанный ⇨ type(x, f) и
men(x, f) не определены
типы вхождения переменных, ≠ х, в f сохраняются по
сравнению с типами вхождения переменных в g

Разрешенная формула
реляционного исчисления кортежей
Формула
g – разрешенная формула
f = (g) ⇨ f – разрешена
типы вхождения переменных в f, а также типы и
множества ссылок, сохраняются по сравнению с
типами вхождения переменных в g
type(x, f) = type(x, g), men(x, f) = men(x, g)

Значение выражения
реляционного исчисления кортежей:
Подстановка
f(x) – разрешенная формула
type(x, f) = R, R⊆U, или men(x, f)⊆R
f(t/x) – подстановка
кортежа t вместо переменной x,
определяемая модификацией ∀ атома,
содержащего свободное вхождение х в f
по правилам:

Значение выражения
реляционного исчисления кортежей:
Подстановка

Значение выражения
реляционного исчисления кортежей
Интерпретация
f(x) – разрешенная формула
∄ свободных переменных в f
I(f) – интерпретация формулы f
f = true ⇨ I(f) = true
f = false ⇨ I(f) = false
f = ¬g, в g ∄ свободных переменных
I(f) = true, если I(g) = false
I(f) = false, если I(g) = true

Значение выражения
реляционного исчисления кортежей
Интерпретация
f(x) – разрешенная формула
∄ свободных переменных в f
I(f) – интерпретация формулы f
f = g ∧ h, в g и h ∄ свободных переменных
I(f) = true, если I(g) = true и I(h) = true,
иначе I(f) = false
f = g ∨ h, в g и h ∄ свободных переменных
I(f) = false, если I(g) = false и I(h) = false,
иначе I(f) = true

Значение выражения
реляционного исчисления кортежей
Интерпретация
f(x) – разрешенная формула
∄ свободных переменных в f
I(f) – интерпретация формулы f
f = ∃x(R)g, х – единственная свободная переменная в g
I(f) = true, если ∃ t ∈ dom(R) : I(g(t/x)) = true,
иначе I(f) = false
f = ∀x(R)g, х – единственная свободная переменная в g
I(f) = true, если ∀ t ∈ dom(R) I(g(t/x)) = true,
иначе I(f) = false
f = (g) ⇨ I(f) = I(g)

Значение выражения
реляционного исчисления кортежей

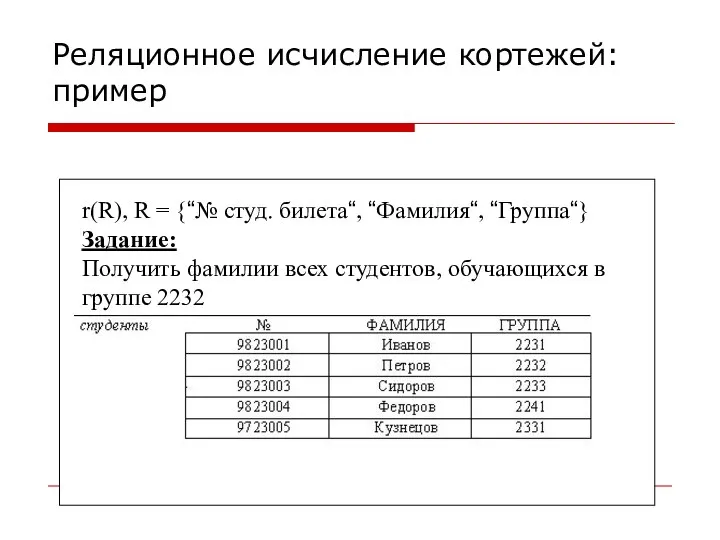
Реляционное исчисление кортежей:
пример
r(R), R = {“№ студ. билета“, “Фамилия“, “Группа“}
Задание:
Получить фамилии всех студентов, обучающихся в
группе 2232

{x(“Фамилия“) | ∃y(R) (r(y) ∧ x(“Фамилия“) =
y(“Фамилия“) ∧ y(“Группа“) = 2232)}
{x(“Фамилия“) | ∃y(R) ∈ r (x(“Фамилия“) =
y(“Фамилия“) ∧ y(“Группа“) = 2232)}
Реляционное исчисление кортежей:
пример

Реляционное исчисление кортежей:
пример

Реляционное исчисление кортежей:
пример

Реляционное исчисление кортежей:
пример

Реляционное исчисление кортежей:
пример

Реляционное исчисление кортежей:
пример