Содержание
- 2. Раздел BOUNDARIES BOUNDARIES Region 1 START(-1,-1) LINE TO(1,-1) TO (1,1) TO (-1,1) TO CLOSE Region 2
- 3. 2D задача
- 4. Понятие экструзии Экстру́зия (от англ. extrusion — выталкивание, выдавливание) В программу (2D-скрипт) необходимо внести следующие изменения:
- 5. Формы записи экструзии
- 6. TITLE 'Heat flow around an Insulating blob' COORDINATES cartesian3 VARIABLES Phi { the temperature } DEFINITIONS
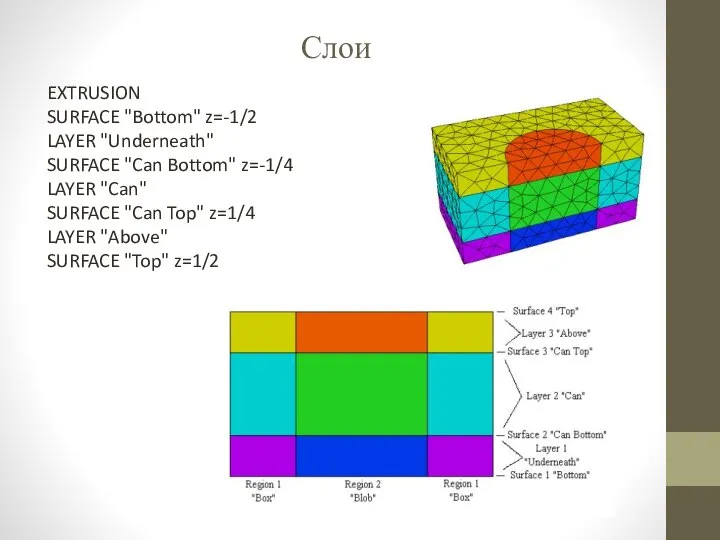
- 7. Слои EXTRUSION SURFACE "Bottom" z=-1/2 LAYER "Underneath" SURFACE "Can Bottom" z=-1/4 LAYER "Can" SURFACE "Can Top"
- 8. Настройка свойств материала по регионам и слоям
- 9. Настройка свойств материала по регионам и слоям
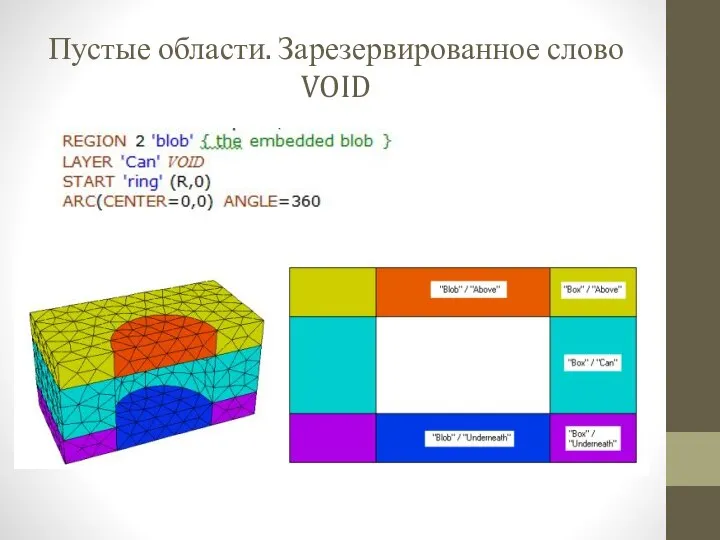
- 10. Пустые области. Зарезервированное слово VOID
- 11. Ограниченные регионы
- 12. Задание плоскости среза Осуществляется добавлением спецификатора ON: PLOTS CONTOUR(Phi) ON x=0 Можно также запросить графики вычислительной
- 13. Задание плоскости среза grid (x,y) on z=0.55
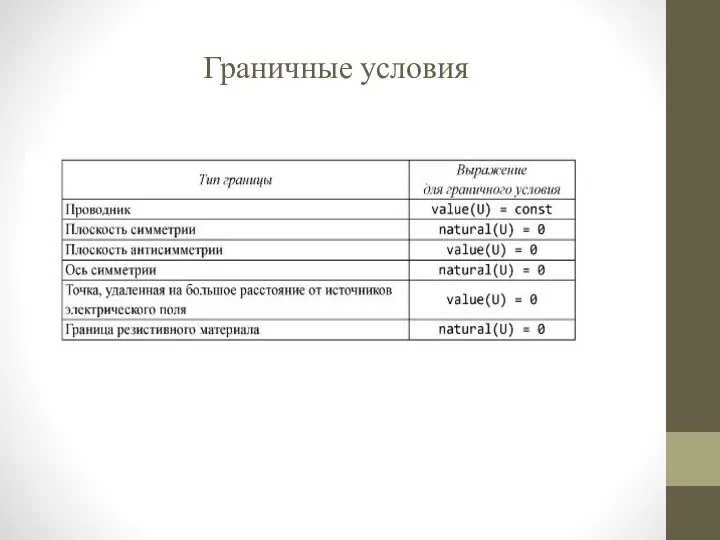
- 14. Граничные условия BOUNDARIES REGION 1 'box' START(-1,-1) VALUE(Phi)=0LINE TO (1,-1) NATURAL(Phi)=0 LINE TO (1,1) VALUE(Phi)=1LINE TO
- 15. Объемные поверхности и слои Фигуры должны поддерживать вытянутую форму, с боковыми стенками и слоями (боковые стенки
- 17. Функции поверхности FlexPDE включает в себя три функции формирования поверхности (плоскость, цилиндр и сфера) для упрощения
- 18. Функции поверхности: цилиндр
- 19. Полусфера
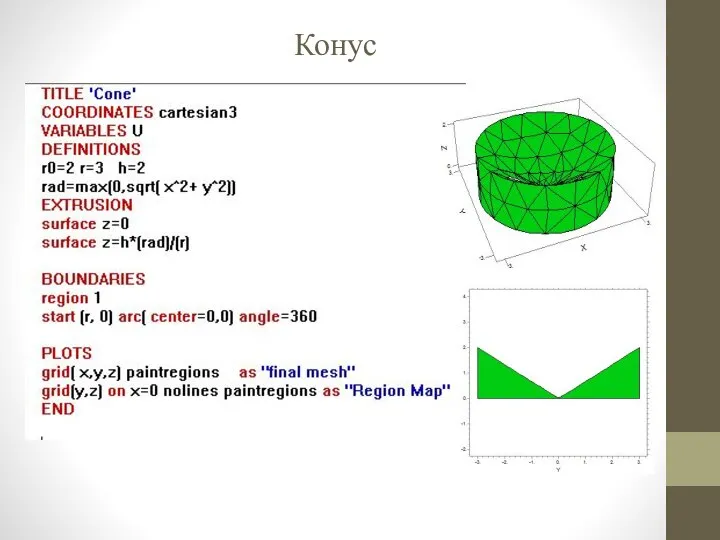
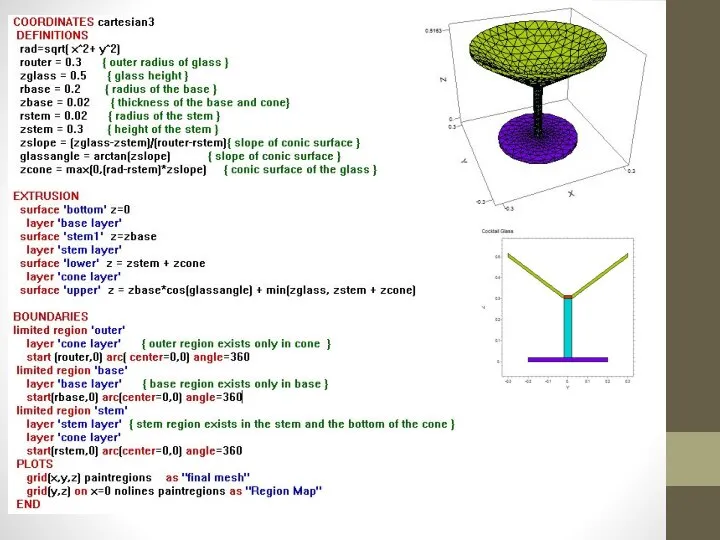
- 21. Конус
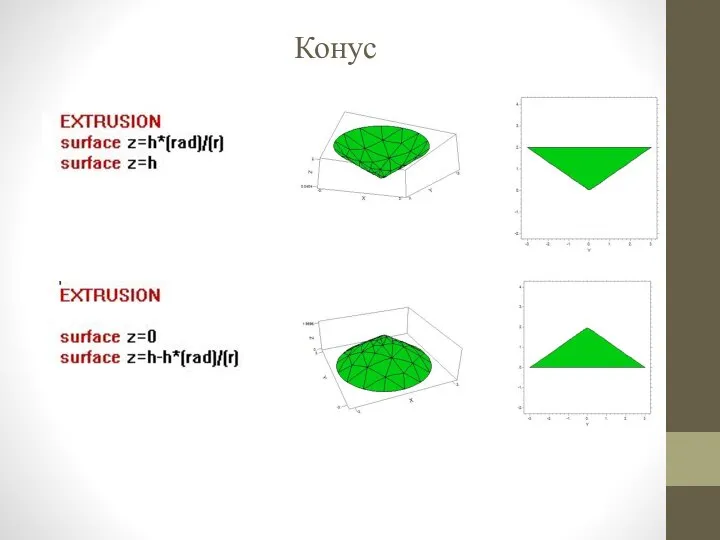
- 22. Конус
- 24. Интегральные операторы Операторы INTEGRAL и VOL_INTEGRAL являются синонимами и производят интегрирование по объему. Формат: INTEGRAL( )
- 25. Поверхностные интегралы Операторы SINTEGRAL и SURF_INTEGRAL являются синонимами и выполняют интегрирование по поверхности. Формат: SINTEGRAL (
- 26. Линейные интегралы Операторы BINTEGRAL и LINE_INTEGRAL являются синонимами и выполняют интегрирование по линии. Форма записи: BINTEGRAL(
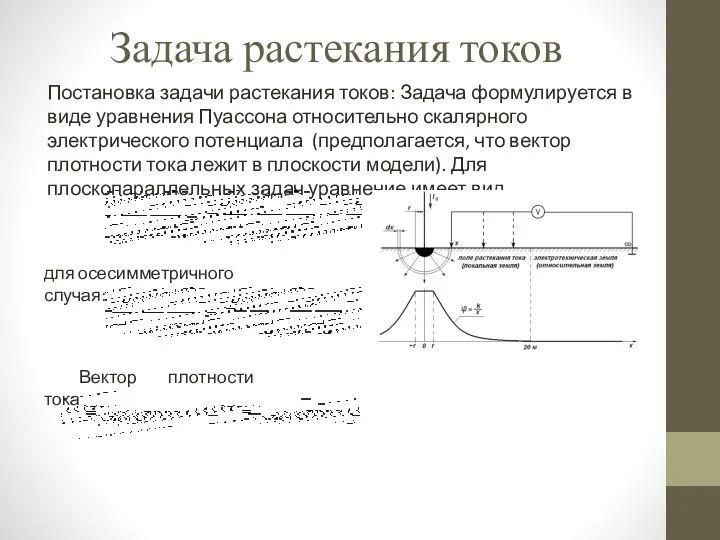
- 27. Задача растекания токов Постановка задачи растекания токов: Задача формулируется в виде уравнения Пуассона относительно скалярного электрического
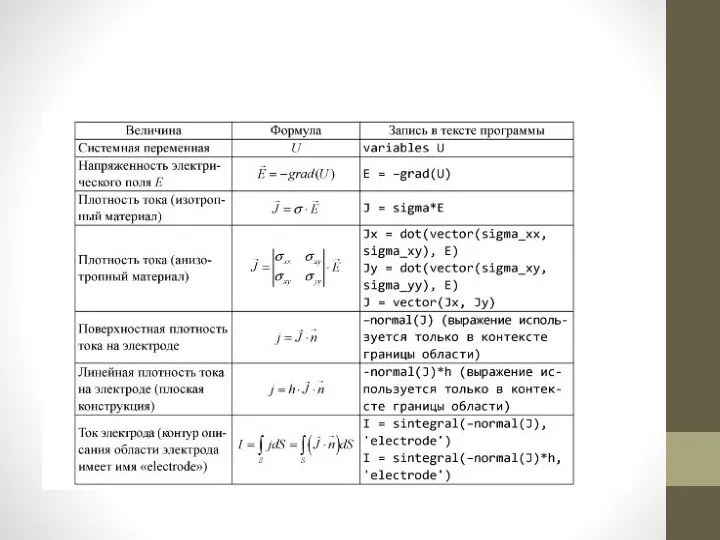
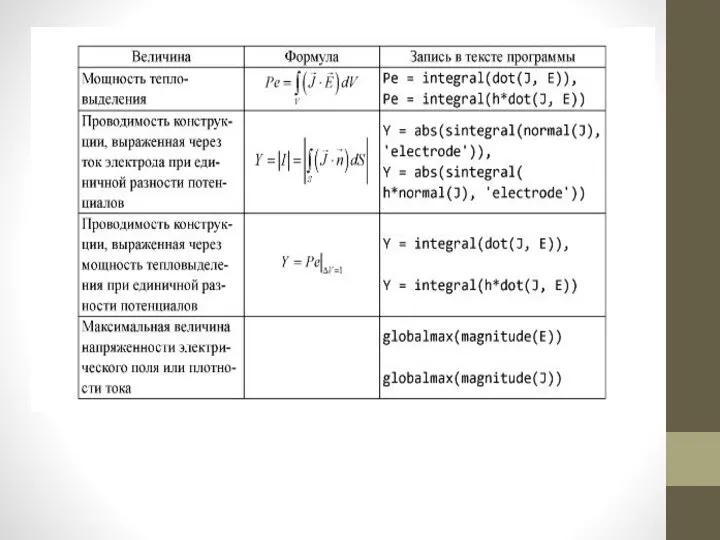
- 28. Вычисляемые физические величины в задачах растекания токов
- 31. Граничные условия
- 32. Пример расчета сопротивлении пленочного резистора
- 33. Пример расчета сопротивлении пленочного резистора
- 35. Скачать презентацию























 Аккаунт экскурсовода-гида
Аккаунт экскурсовода-гида Информационная безопасность персональных компьютеров
Информационная безопасность персональных компьютеров J7 апдейт верстки Полезный завтрак
J7 апдейт верстки Полезный завтрак Simulink. Компьютерные технологии при разработке и проектировании электрооборудования автономных объектов
Simulink. Компьютерные технологии при разработке и проектировании электрооборудования автономных объектов Проект. Григорианский пролептический календарь
Проект. Григорианский пролептический календарь Системы в нашей жизни
Системы в нашей жизни Источники справочной информации по диагностике сетей
Источники справочной информации по диагностике сетей 2 дома 2 (1)
2 дома 2 (1) Сбалансированные показатели сайтов
Сбалансированные показатели сайтов УЦ УГМК-Холдинг
УЦ УГМК-Холдинг Сайт музыкальной школы
Сайт музыкальной школы История развития вычислительной техники
История развития вычислительной техники Код Хаффмана
Код Хаффмана Lineage 2 - многопользовательская ролевая онлайн-игра для платформы Microsoft Windows
Lineage 2 - многопользовательская ролевая онлайн-игра для платформы Microsoft Windows Android
Android Создание функции, аргументы, параметры, возвращение результата
Создание функции, аргументы, параметры, возвращение результата АРМ геолога: ПО применяемое в геологии
АРМ геолога: ПО применяемое в геологии Презентация на тему Информация и информационные процессы в технике
Презентация на тему Информация и информационные процессы в технике  Обратная связь на всех этапах разработки програмных средств
Обратная связь на всех этапах разработки програмных средств Презентация на тему Информационные модели систем управления
Презентация на тему Информационные модели систем управления  Методы и технологии конструирования изделий. Основы геометрического моделирования деталей. (Лекция 2)
Методы и технологии конструирования изделий. Основы геометрического моделирования деталей. (Лекция 2) Тенденции развития программного обеспечения
Тенденции развития программного обеспечения 171050c0d77745468ac9eed15021cb0d
171050c0d77745468ac9eed15021cb0d Возможности НКО Карелии по информационному сопровождению своей деятельности
Возможности НКО Карелии по информационному сопровождению своей деятельности Паскаль_ЧислМетоды
Паскаль_ЧислМетоды Интерактивные элементы в дизайн макетах
Интерактивные элементы в дизайн макетах Работа с источниками информации. Работа с электронными каталогами и поисковыми системами
Работа с источниками информации. Работа с электронными каталогами и поисковыми системами Работа в https://learningapps.org
Работа в https://learningapps.org