Симметричное шифрование AES Rijndael

История проведения конкурса AES
В 1997 году правительство США объявило на базе института стандартизации NIST (the National Institute of Standards and Technology) открытый конкурс на новый стандарт блочного шифра США. Победитель конкурса получал статус нового стандарта шифрования AES (Advanced Encryption Standard) и рекомендовался к повсеместному использованию на территории США.

Требования, которые
предъявлялись к новому стандарту:
криптоалгоритм должен быть открыто опубликован;
криптоалгоритм должен быть симметричным блочным шифром, поддерживающим 128-, 192- и 256-битные ключи.
криптоалгоритм должен быть предназначен как для аппаратной, так и для программной реализации;
криптоалгоритм должен быть доступен для открытого использования в любых продуктах, а значит, не может быть запатентован, в противном случае патентные права должны быть аннулированы;
криптоалгоритм подвергается изучению по следующим параметрам: стойкости, стоимости, гибкости, реализуемости в smart-картах.
Претендентов конкурса AES было множество, но многие имели свои криптографические недостатки

Некоторые претенденты конкурса AES

Некоторые претенденты конкурса AES

Некоторые претенденты конкурса AES
Winner

Основные массивы данных
Входными данными для операций шифрования есть массив из 16 байт. Перед началом шифрования байты этого массива размещаются последовательно в столбцы матрицы InputBlock (сверху вниз). Внутри алгоритма операции выполняются над матрицей байт, называемой матрицей состояний State или просто состоянием. Конечное значение матрицы состояния OutputBlock является выходом алгоритма и преобразуется в последовательность байтов шифротекста. Аналогично в столбцы матрицы InputKey попадают и 16 байтов ключа шифра.
InputBlock
State
OutputBlock

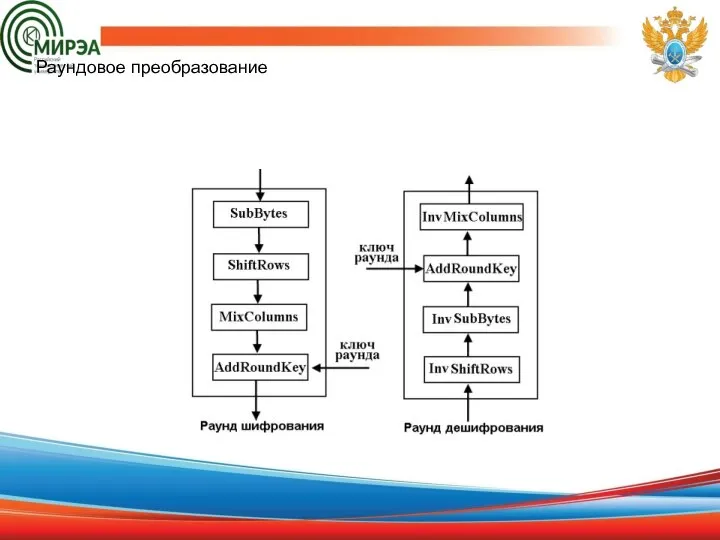
Раундовое преобразование
Раунд состоит из четырех различных преобразований:
замена байтов SubBytes() – побайтовой подстановки в S-блоках с фиксированной таблицей замен размерностью 8x256;
сдвига строк ShiftRows() – побайтового сдвига строк массива State на различное количество байт;
перемешивание столбцов MixColumns() – умножение столбцов состояния, рассматриваемых как многочлены над GF(28), на многочлен третьей степени g(x) по модулю x4+1;
сложение с раундовым ключом AddRoundKey() – поразрядного XOR с текущим фрагментом развернутого ключа.

Раундовое преобразование

Операции в поле GF(28)

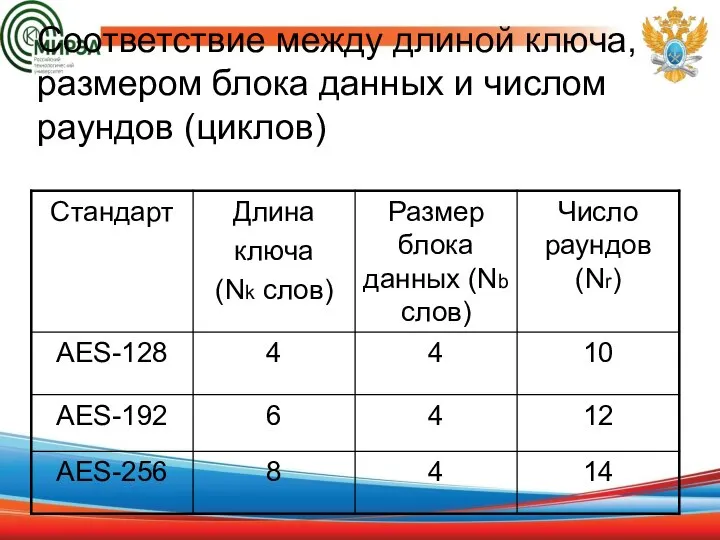
Соответствие между длиной ключа, размером блока данных и числом раундов (циклов)

Применение преобразования SubBytes()
Преобразование представляет собой нелинейную замену байт, выполняемую независимо с каждым байтом состояния. Таблицы замены (или S-блоки) являются инвертируемыми и построены из композиции двух преобразований:
1. Получение обратного элемента относительно умножения в поле GF(28), принято считать, что комбинация '00' переходит сам в себя.
2. Применение афинного преобразования (над GF(2)), определенного как:
через x обозначены входные биты, а через y – выходные

Преобразования SubBytes()
Суть преобразования может быть описана уравнением
yi=xi ⊕ x(i+4)mod8⊕x(i+5)mod8 ⊕ x(i+6)mod8 ⊕ x(i+7)mod8 ⊕ ci,
где c0=c1=c5=c6=1, c2=c3=c4=c7=0, bi и bi’-соответственно исходное и преобразованное значение i-го бита, i меняется от 0 до 7.

Преобразования SubBytes() - пример

Например, если s1,1={8A}, то результат замены этого байта следует искать на пересечении строки с индексом 8 и столбца с индексом A, т.е. SubBytes(8A)={7E}.
S-блок

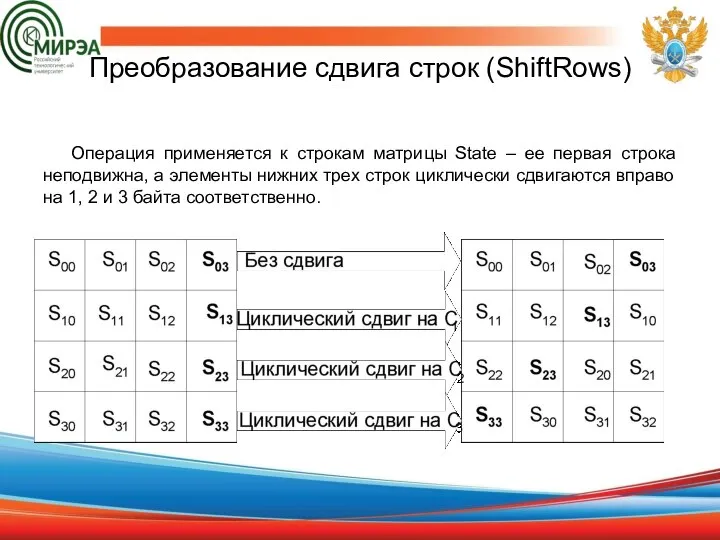
Преобразование сдвига строк (ShiftRows)
Операция применяется к строкам матрицы State – ее первая строка неподвижна, а элементы нижних трех строк циклически сдвигаются вправо на 1, 2 и 3 байта соответственно.

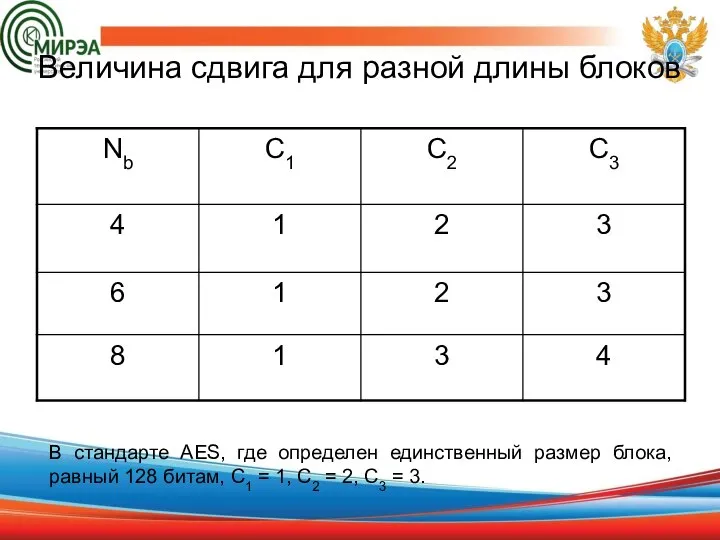
Величина сдвига для разной длины блоков
В стандарте AES, где определен единственный размер блока, равный 128 битам, С1 = 1, С2 = 2, С3 = 3.

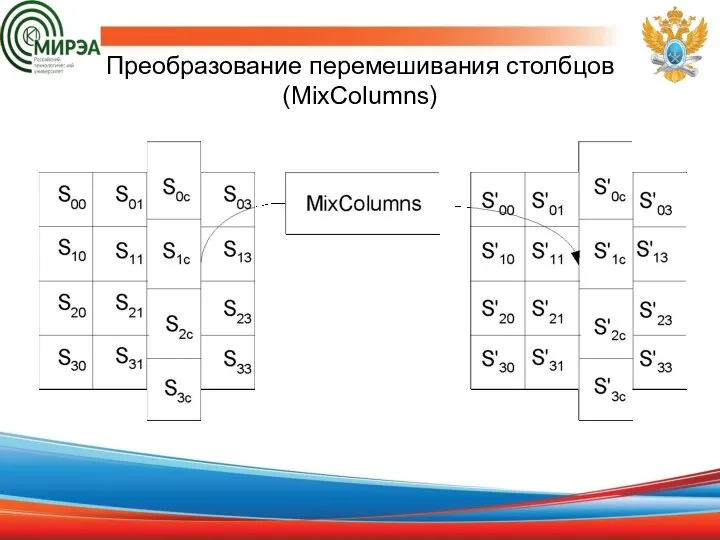
Преобразование перемешивания столбцов (MixColumns)

Преобразование перемешивания столбцов (MixColumns) - это такое преобразование, при котором столбцы состояния рассматриваются как многочлены над GF(28) и умножаются по модулю х4+1 на многочлен c(x), выглядящий следующим образом:
Это может быть представлено в матричном виде следующим образом:
Преобразование перемешивания столбцов (MixColumns)
где с – номер столбца массива State.

В результате такого умножения байты столбца s0, s1, s2, s3 заменяются соответственно на байты:
s’0=({02}*s0)⊕({03}*s1) ⊕s2⊕s3,
s’1=s0⊕({02}*s1) ⊕({03}*s2) ⊕s3,
s’2=s0⊕s1⊕({02}*s2) ⊕({03}*s3),
s’3=({03}*s0) ⊕s1⊕s2⊕({02}*s3).
Преобразование перемешивания столбцов (MixColumns)

Добавление раундового ключа (AddRoundKey)
AddRoundKey(State, RoundKey) побитово складывает элементы переменной RoundKey и элементы переменной State по принципу: i-й столбец данных (i = 0, 1, 2, 3) складывается с определенным 4-байтовым фрагментом расширенного ключа W=[4r+1], где r – номер поточного раунда алгоритма. При шифровании первое сложение ключа раунда происходит до первого выполнения операции SubBytes.

Алгоритм выработки ключей
Раундовые ключи получаются из ключа шифрования посредством алгоритма выработки ключей. Он содержит два компонента: расширение ключа (Key Expansion) и выбор раундового ключа (Round Key Selection).
Основополагающие принципы алгоритма выглядят следующим образом:
общее число битов раундовых ключей равно длине блока, умноженной на число раундов, плюс 1 (например для длины блока 128 бит и 10 раундов требуется 1408 бит раундовых ключей);
ключ шифрования преобразуется в расширенный ключ (Expanded Key);
раундовые ключи берутся из расширенного ключа следующим образом: первый раундовый ключ содержит первые Nb слов, второй – следующие Nb слов и т. д.
Расширенный ключ (Key Expansion) в Rijndael представляет собой линейный массив w[i] из Nb(Nr+1) 4-байтовых слов.
Первые Nk слов содержат ключ шифрования. Все остальные слова определяются рекурсивно из слов с меньшими индексами. Алгоритм выработки подключей зависит от величины Nk.
Первые Nk слов заполняются ключом шифрования. Каждое последующее слово w[i] получается посредством сложения по модулю два предыдущего слова w[i-1] и слова на Nk позиций ранее, то есть w[i-Nk]:
w[i] = w[i-1] ⊕ w[i-Nk].

Алгоритм выработки ключей
Для слов, позиция которых кратна Nk перед операцией сложения по модулю два применяется преобразование к w[i-1], а затем еще прибавляется раундовая константа Rconst. Преобразование реализуется с помощью двух дополнительных функций: RotWord(), осуществляющей побайтовый сдвиг 32-разрядного слова по формуле {a0, a1, a2, a3} → {a1, a2, a3, a0}, и SubWord(), осуществляющей побайтовую замену с использованием S-блока функции SubBytes(). Значение Rconst[j] равно2j-1. Значение w[i] в этом случае равно:
w[i] = SubWord(RotWord(w[i-1])) ⊕ Rconst[i/Nk] ⊕ w[i-Nk].
Раундовый ключ i получается из слов массива раундового ключа от W[Nbi] и до W[Nb(i+1)].

Функция обратного дешифрования
Если вместо SubBytes(), ShiftRows(), MixColumns() и AddRoundKey() в обратной последовательности выполнить инверсные им преобразования, можно построить функцию обратного дешифрования. При этом порядок использования раундовых ключей является обратным по отношению к тому, который используется при зашифровании.
Функция AddRoundKey() обратна сама себе, учитывая свойства используемой в ней операции XOR.
Для преобразования байта {xy} используется инверсный S-блок InvSubBytes
В преобразовании InvShiftRows последние 3 строки состояния сдвигаются вправо на различное число байтов. Строка 1 сдвигается на С1 байт, строка 2 – на С2 байт, и строка 3 – на С3 байт. Значение сдвигов С1, С2 и С3 зависят от длины блока Nb.

Функция обратного дешифрования
В преобразовании InvMixColumns столбцы состояния рассматриваются как многочлен над GF(28) и умножаются по модулю x4+1 на многочлен g-1(x), выглядящий следующим образом:
g-1(x)={0b}x3+{0d}x2+{09}x+{0e}.
Это может быть представлено в матричном виде следующим образом:
В результате на выходе получаются следующие байты:
s’0c=({0e}*s0c)⊕({0b}*s1c)⊕({0d}*s2c)⊕({09}*s3c),
s’1c=({09}*s0c)⊕({0e}*s1c)⊕({0b}*s2c)⊕({0d}*s3c),
s’2c=({0d}*s0c)⊕({09}*s1c)⊕({0e}*s2c)⊕({0b}*s3c),
s’3c=({0b}*s0c)⊕({0d}*s1c)⊕({09}*s2c)⊕({0e}*s3c).

Основные особенности Rijndael
новая архитектура «Квадрат», обеспечивающая быстрое рассеивание и перемешивание информации, при этом за один раунд преобразованию подвергается весь входной блок;
байт ориентированная структура, удобная для реализации на 8-разрядных МК;
все раундовые преобразования представляют собой операции в конечных полях, допускающие эффективную аппаратную и программную реализацию на различных платформах.