Содержание
- 2. Цели занятия: 1) Закрепить понятия «число», «цифра» 2) Раскрыть понятия «система счисления», «алфавит» системы счисления 3)
- 3. Содержание 1. Основные понятия. Виды систем счисления 2. Непозиционные системы счисления 3. Позиционные системы счисления 4.
- 4. Основные понятия Система счисления - это способ записи чисел и правила действий над этими числами Число
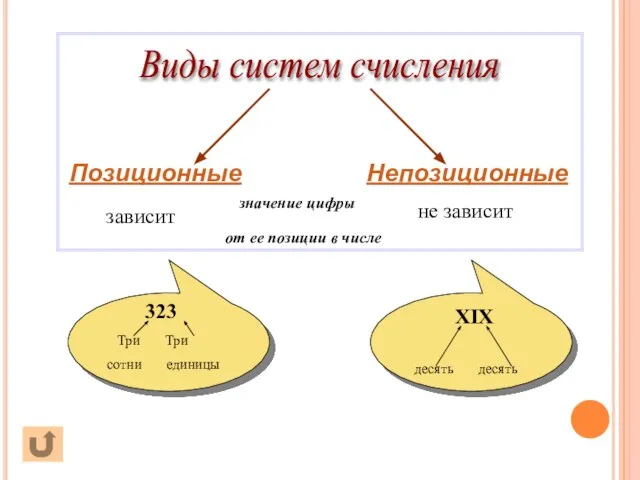
- 5. зависит не зависит
- 6. Непозиционные системы счисления
- 8. = 3 4 5
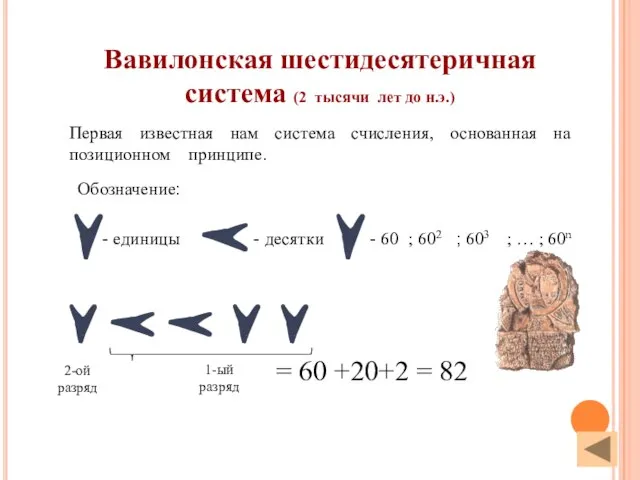
- 9. = 60 +20+2 = 82
- 10. X X X I I = 32 D X L I I = 542 Найдите значения
- 12. – основание (p) Совокупность всех цифр – алфавит Позиционные системы могут иметь различный алфавит (2,3,4 знака).
- 13. Алфавиты систем счисления Для записи чисел в позиционной системе с основанием р нужно иметь алфавит из
- 14. ПРИМЕРЫ: (перепиши, вставляя пропущенные числа) p = 10 (десятичная с/c) 1 2 3 4 5 6
- 16. Система счисления, применяемая в современной математике, является позиционной десятичной системой. Её основание равно десяти, т.к. запись
- 17. Рассмотрим десятичное число 555: 5 5 5 10 единицы десятки сотни Из двух написанных рядом одинаковых
- 18. В развернутой форме записи числа умножение цифр производится в явной форме: 55510 = 5·102 + 5·101
- 20. Двоичная система счисления является позиционной системой счисления. Алфавит двоичной системы – две цифры (0,1), основание равно
- 21. В развернутой форме число записывается в виде суммы ряда степеней основания 2 с коэффициентами, в качестве
- 22. Восьмеричная система счисления является позиционной системой счисления. Алфавит восьмеричной системы – цифры (0,1,2,3,4,5,6,7), основание равно 8.
- 23. В развернутой форме число записывается в виде суммы ряда степеней основания 8 с коэффициентами, в качестве
- 24. Шестнадцатеричная система счисления является позиционной системой счисления. Алфавит шестнадцатеричной системы – цифры (0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F), основание равно 16.
- 25. В развернутой форме число записывается в виде суммы ряда степеней основания 16 с коэффициентами, в качестве
- 26. Алгоритм перевода чисел, записанных в произвольной системе счисления, в десятичную систему счисления 1. Записать число в
- 27. Задания для самостоятельного выполнения Задание 1 Задание 2 Задание 3 Задание 4 Задание 5 Задание 6
- 28. Ответ: а) 341 (р=5) в) 222 (р=3) б) 123 (р=4) г) 111 (р=2) Какое минимальное основание
- 29. Ответ: а) в троичной СС для записи чисел используются цифры 0 1 2 , значит цифры
- 30. Ответ: 11112 = 1510. Какое максимальное число можно записать в двоичной системе счисления четырьмя цифрами? Переведите
- 31. Ответ: четное число в двоичной системе счисления оканчивается на 0, а нечетное – на 1. а)
- 32. Ответ: да, если считать числа в задаче, представленными в двоичной системе счисления: 112= 1⋅21 + 1⋅20
- 34. Скачать презентацию




























 Информация и информационные процессы
Информация и информационные процессы Базовые типы и операторы
Базовые типы и операторы Системы программирования
Системы программирования Информационная безопасность. Основные понятия
Информационная безопасность. Основные понятия Инструкция по работе с ЭБС BOOK.RU
Инструкция по работе с ЭБС BOOK.RU Дисциплина Информатика и ИКТ. Структура курса
Дисциплина Информатика и ИКТ. Структура курса Операции над высказываниями 2021
Операции над высказываниями 2021 Сборки. Атрибуты
Сборки. Атрибуты Заявка на встречу с дизайнером. Описание кнопок и страниц
Заявка на встречу с дизайнером. Описание кнопок и страниц Правила безопасного поведения в Интернете
Правила безопасного поведения в Интернете Overview. Simulation
Overview. Simulation Методы обеспечивающие безопасность информации
Методы обеспечивающие безопасность информации Clasno. Главная. Личный кабинет
Clasno. Главная. Личный кабинет Вебасембли
Вебасембли Задачи математического программирования
Задачи математического программирования Презентация по информатике на тему _Аппаратное и программное обеспечение компьютера_, 11 класс
Презентация по информатике на тему _Аппаратное и программное обеспечение компьютера_, 11 класс Запись видео мастер-класса в дистанционной форме. Магнит-одуванчик
Запись видео мастер-класса в дистанционной форме. Магнит-одуванчик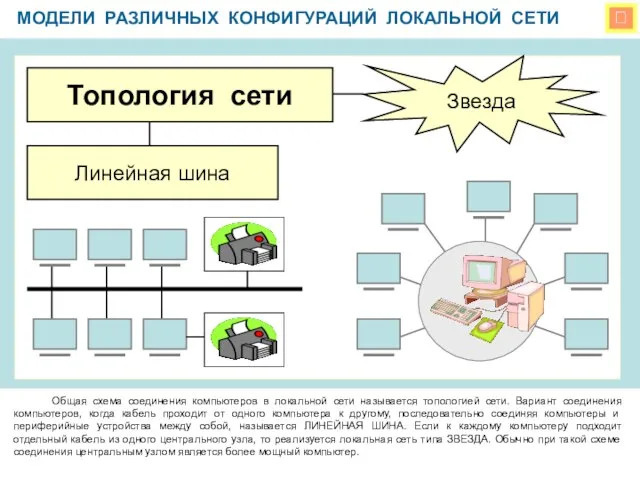 Модели различных конфигураций локальной сети
Модели различных конфигураций локальной сети Инструкция по регистрации
Инструкция по регистрации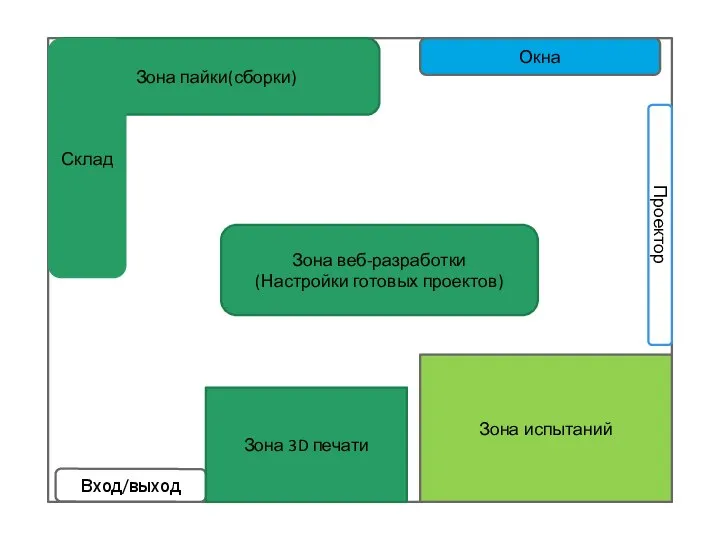 Веб-лаболотория - WPS Office
Веб-лаболотория - WPS Office Партнерская программа ООО АльянсАвтоГрупп
Партнерская программа ООО АльянсАвтоГрупп Разработка базы данных преприятия
Разработка базы данных преприятия Качество программного продукта (Software Quality)
Качество программного продукта (Software Quality) Кодирование информации
Кодирование информации Компьютерный вирус
Компьютерный вирус Системы счисления. Логика и алгоритмы. Высказывания, логические операции, кванторы, истинность высказывания
Системы счисления. Логика и алгоритмы. Высказывания, логические операции, кванторы, истинность высказывания Электронные таблицы: общие сведения
Электронные таблицы: общие сведения Переход от реального объекта к 3Д-анимации
Переход от реального объекта к 3Д-анимации