числа и получаемых неполных частных на основание новой системы счисления до тех пор, пока не получим неполное частное, меньшее делителя;
2) полученные остатки, являющиеся цифрами числа в новой системе счисления, привести в соответствие с алфавитом новой системы счисления;
3) составить число в новой системе счисления, записывая его, начиная с последнего частного.
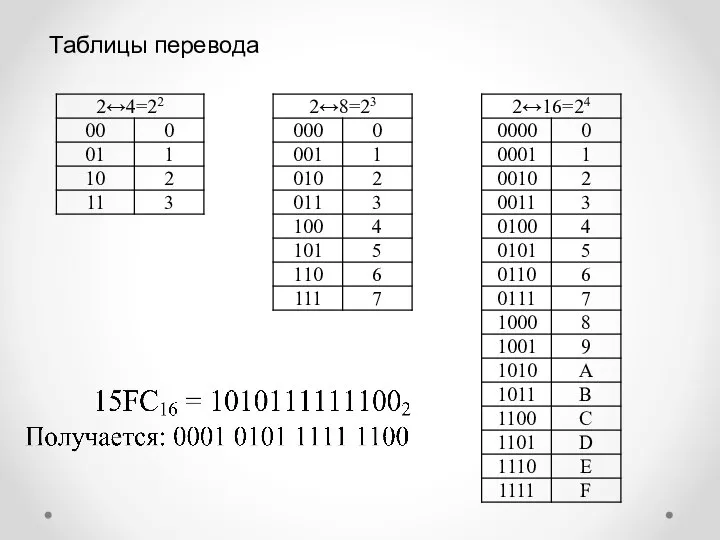
Пример. Перевести десятичное число 315 в восьмеричную и в шестнадцатеричную системы:
Отсюда следует: 31510 = 4738 = 13В16. Напомним, что 1110 = В16.








 Разработать программный продукт для предприятия ПАО МРСК Волги - Оренбургэнерго
Разработать программный продукт для предприятия ПАО МРСК Волги - Оренбургэнерго Проектирование пользовательского интерфейса графической оболочки сайта учебного учреждения АНПОО РОСТ
Проектирование пользовательского интерфейса графической оболочки сайта учебного учреждения АНПОО РОСТ Интегрированный урок информатики и литературы
Интегрированный урок информатики и литературы Интегрированный урок физики и информатики в 9 классе
Интегрированный урок физики и информатики в 9 классе Обчислювальні кластери в корпоративній мережі. Їх архітектура
Обчислювальні кластери в корпоративній мережі. Їх архітектура Вспомогательный алгоритм или процедура
Вспомогательный алгоритм или процедура Игра: фэйлол
Игра: фэйлол GPS/Glonass мониторинг. Задачи и функции системы
GPS/Glonass мониторинг. Задачи и функции системы Разработка автоматизированной системы формирования оптимального портфеля заказов предприятия
Разработка автоматизированной системы формирования оптимального портфеля заказов предприятия Информационное обеспечение компьютерных технологий
Информационное обеспечение компьютерных технологий Insribe Reader
Insribe Reader Регистрация магазина на StoreLand и выбор шаблона
Регистрация магазина на StoreLand и выбор шаблона Целочисленное деление (div) и деление с остатком (mod)
Целочисленное деление (div) и деление с остатком (mod) Киберпреступность. Основы проектной деятельности
Киберпреступность. Основы проектной деятельности Программа для робота шпиона. Лего
Программа для робота шпиона. Лего Целочисленные алгоритмы (язык Си)
Целочисленные алгоритмы (язык Си) Линейный свет и цветовой контраст
Линейный свет и цветовой контраст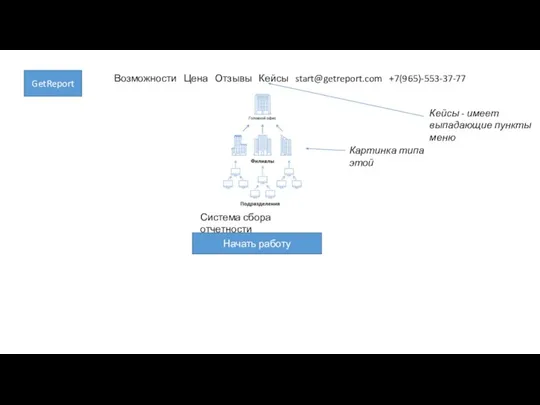 Система сбора отчетности
Система сбора отчетности Система мониторинга для организации
Система мониторинга для организации Презентация на тему Оперативная память
Презентация на тему Оперативная память  тестирование смэв 2022
тестирование смэв 2022 На чем написано
На чем написано Дополнительные устройства компьютера
Дополнительные устройства компьютера Оформление библиографического описания
Оформление библиографического описания Решение задач на компьютере. Алгоритмизация и программирование. 9 класс
Решение задач на компьютере. Алгоритмизация и программирование. 9 класс Massenmedien: Fernsehen
Massenmedien: Fernsehen Homework assignment
Homework assignment Шаблон для презинтаций
Шаблон для презинтаций