Системы счисления информатика для СПО

ЧТО ТАКОЕ СИСТЕМА СЧИСЛЕНИЯ?
Система счисления — это правила записи чисел с помощью специальных знаков — цифр, а также соответствующие правила выполнения операций с этими числами.

НЕМНОГО ИСТОРИИ
Счёт на пальцах:

УНАРНАЯ СИСТЕМА
Унарная (лат. unus – один) – одна цифра обозначает единицу (1 день, 1 камень, 1 баран, …)
только натуральные числа
запись больших чисел – длинная (1 000 000?)
Уна́рная (едини́чная, ра́зная) систе́ма счисле́ния — непозиционная система счисления с единственной цифрой, обозначающей 1.

НЕПОЗИЦИОННАЯ СИСТЕМА СЧИСЛЕНИЯ
В непозиционных системах счисления величина, которую обозначает цифра, не зависит от положения в числе. При этом система может накладывать ограничения на положение цифр, например, чтобы они были расположены в порядке убывания.

НЕПОЗИЦИОННЫЕ СИСТЕМЫ СЧИСЛЕНИЯ
унарная
египетская десятичная
римская
славянская
и другие…

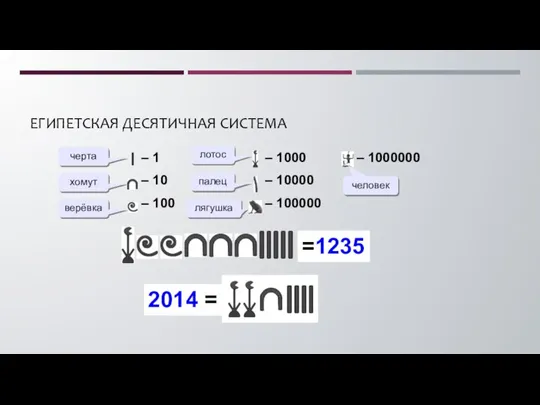
ЕГИПЕТСКАЯ ДЕСЯТИЧНАЯ СИСТЕМА
– 1
– 10
– 100
– 1000
– 10000
– 100000
– 1000000
черта
хомут
верёвка
лотос
палец
лягушка
человек
= ?
=1235
2014 = ?

РИМСКАЯ СИСТЕМА СЧИСЛЕНИЯ
I – 1 (палец),
V – 5 (раскрытая ладонь, 5 пальцев),
X – 10 (две ладони),
L – 50,
C – 100 (Centum),
D – 500 (Demimille),
M – 1000 (Mille)

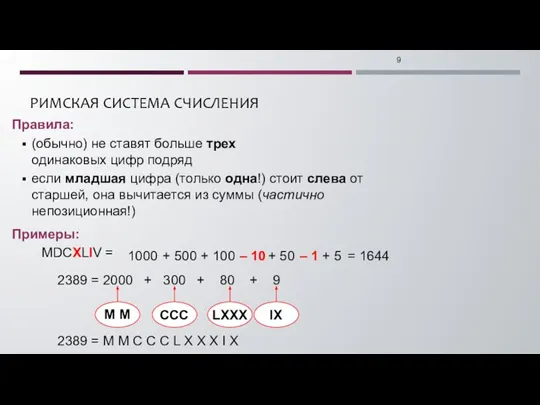
РИМСКАЯ СИСТЕМА СЧИСЛЕНИЯ
Правила:
(обычно) не ставят больше трех
одинаковых цифр подряд
если младшая цифра (только одна!) стоит слева от старшей, она вычитается из суммы (частично непозиционная!)
Примеры:
MDCXLIV =
1000
+ 500
+ 100
– 10
+ 50
– 1
+ 5
2389 = 2000 + 300 + 80 + 9
2389 = M M C C C L X X X I X
M M
CCC
LXXX
IX
= 1644

РИМСКАЯ СИСТЕМА СЧИСЛЕНИЯ
MCDLXVII =
MMDCXLIV =
MMMCCLXXII =
CMXXVIII =

РИМСКАЯ СИСТЕМА СЧИСЛЕНИЯ
CMXCIV =
MMMCDXLIX =
MCMXLIX =
MMCDXCIX =

РИМСКАЯ СИСТЕМА СЧИСЛЕНИЯ
3768 =
2983 =
1452 =
1999 =

РИМСКАЯ СИСТЕМА СЧИСЛЕНИЯ
1468 =
1383 =
1152 =
1099 =

НЕДОСТАТКИ РИМСКОЙ СИСТЕМЫ СЧИСЛЕНИЯ
можно записывать только натуральные числа;
чтобы записывать большие числа, необходимо вводить все новые и новые цифры;
сложно выполнять арифметические действия.

СЛАВЯНСКАЯ СИСТЕМА СЧИСЛЕНИЯ
Система записи чисел кириллицей, цифи́рь — способ записи чисел алфавитной записи чисел с использованием кириллицы или глаголицы, использовавшийся в Древней Руси.

ПОЗИЦИОННЫЕ СИСТЕМЫ СЧИСЛЕНИЯ
Позиционная система: значение цифры определяется ее позицией в записи числа.
Алфавит системы счисления — это используемый в ней набор цифр.
Основание системы счисления — это количество цифр в алфавите (мощность алфавита).
Разряд — это позиция цифры в записи числа. Разряды в записи целых чисел нумеруются с нуля справа налево.

ФОРМЫ ЗАПИСИ ЧИСЕЛ
6 3 7 5
3 2 1 0
разряды
5
70
300
= 6·103 + 3·102 + 7·101 + 5·100
6000
развёрнутая форма записи числа
Схема Горнера:
6 3 7 5 = ((6⋅10 + 3)⋅10 + 7)⋅10 + 5
для вычислений не нужно использовать возведение в степень
удобна при вводе чисел с клавиатуры, начиная с первой

ПЕРЕВОД В ДЕСЯТИЧНУЮ СИСТЕМУ СЧИСЛЕНИЯ
a3a2a1a0 = a3⋅p 3 + a2⋅p 2 + a1⋅p 1 + a0⋅p 0
Через развёрнутую запись:
Через схему Горнера:
12345 = 1⋅53 + 2⋅52 + 3⋅51 + 4⋅50 = 194
=1
разряды: 3 2 1 0
разряды: 3 2 1 0
a3a2a1a0 = ((a3⋅p + a2)⋅p + a1)⋅p + a0
12345 = ((1⋅5 + 2)⋅5 + 3)⋅5 + 4 = 194
основание системы счисления

ПЕРЕВЕСТИ В ДЕСЯТИЧНУЮ СИСТЕМУ СЧИСЛЕНИЯ
10425 =
10548 =
1010012 =
1010123=
F23A16 =

ПЕРЕВОД ИЗ ДЕСЯТИЧНОЙ В ЛЮБУЮ
194 = 12345 = ((1⋅5 + 2)⋅5 + 3)⋅5 + 4
делится на 5
остаток от деления на 5
a3a2a1a0 = ((a3⋅p + a2)⋅p + a1)⋅p + a0
остаток от деления на p
a3a2a1 = (a3⋅p + a2)⋅p + a1
частное от деления на p

ПЕРЕВОД ИЗ ДЕСЯТИЧНОЙ В ЛЮБУЮ
194
194 = 12345
10 → 5
Делим число на p, отбрасывая остаток
на каждом шаге, пока не получится 0. Затем надо выписать найденные остатки в обратном порядке.

АЛГОРИТМ ПЕРЕВОДА ЦЕЛОЙ ЧАСТИ ВЕЩЕСТВЕННОГО ЧИСЛА ИЗ ДЕСЯТИЧНОЙ СИСТЕМЫ СЧИСЛЕНИЯ В ДРУГУЮ ПОЗИЦИОННУЮ СИСТЕМУ
Целую часть числа (N) разделить нацело на p с остатком. Записать частное и остаток.
Если частное больше p, разделить его на p и записать частное и остаток
Повторять пункт 2 до тех пор, пока частное не станет меньше p
В новой системе счисления целая часть будет записываться из последнего частного, которое будет цифрой старшего разряда, и всех остатков, записанных в порядке обратном порядку их получения.

ПЕРЕВЕСТИ ИЗ ДЕСЯТИЧНОЙ СИСТЕМЫ СЧИСЛЕНИЯ
10 → 5
256;114;17;354;1265
10 → 8
64;112;27;364;2265
10 → 3
999;1205;1702;3541;3265
10 → 7
261;141;17;354;1265

ЗАДАЧИ
Задача: в некоторой системе счисления число 71 записывается как «56x»? Определите основание системы счисления X.
71 = 56X

РЕШЕНИЕ ЗАДАЧИ
в записи есть цифра 6, поэтому X > 6
переводим правую часть в десятичную систему
решаем уравнение
71 = 56X
71 = 5·X + 6
X = 13
1 0
56x
= 5·X1 + 6·X0
= 5·X + 6
Задача: в некоторой системе счисления число 71 записывается как «56x»? Определите основание системы счисления X.

в записи есть цифра 5, поэтому X > 5
переводим правую часть в десятичную систему
решаем уравнение
ЗАДАЧИ
Задача: в некоторой системе счисления число 71 записывается как «155x»? Определите основание системы счисления X.
71 = 155X
2 1 0
155x
= 1·X2 + 5·X1 + 5·X0
= X2 + 5·X + 5
71 = X2 + 5·X + 5
X = 6
X = -11

ПРИМЕРЫ ЗАДАЧ
В системе счисления с некоторым основанием десятичное число 27 записывается в виде 30. Укажите это основание.
В системе счисления с некоторым основанием десятичное число 13 записывается в виде 111. Укажите это основание.
В системе счисления с некоторым основанием десятичное число 12 записывается в виде 110. Укажите это основание.
В системе счисления с некоторым основанием десятичное число 129 записывается в виде 1004. Укажите это основание.
В системе счисления с некоторым основанием десятичное число 30 записывается в виде 110. Укажите это основание.

ПРИМЕРЫ ЗАДАЧ
Запись числа 2105 в системе счисления с основанием N выглядит так 313N.Укажите основание N этой системы счисления
Запись числа 658 в системе счисления с основанием N выглядит так 311N.Укажите основание N этой системы счисления
Чему равно число х, если выполнено равенство 25х+172х=135х

ЗАДАЧИ
Задача: найдите все основания систем счисления, в которых запись десятичного числа 24 оканчивается на 3.
24 = k·X + 3
21 = k·X
X = 3, 7, 21

ЗАДАЧИ
Задача: найдите все десятичные числа,
не превосходящие 40, запись которых в системе счисления с основанием 4 оканчивается на 11.
N = k·42 + 1·4 + 1 = k·16 + 5
При k =0, 1, 2, 3, … получаем
N = 5, 21, 37, 53, …

ПРИМЕРЫ ЗАДАЧ
найдите все основания систем счисления, в которых запись десятичного числа 40 оканчивается на 7.
найдите все основания систем счисления, в которых запись десятичного числа 17 оканчивается на 5.
найдите все основания систем счисления, в которых запись десятичного числа 42 оканчивается на 6.
Найдите все основания системы счисления, в которых запись числа 29 оканчивается на 5.
Найдите все десятичные числа, не превосходящие 25, запись которых в двоичной системе счисления оканчивается на 101

ЗАДАЧИ
Задача: Все 5-буквенные слова, составленные из букв А, О и У, записаны в алфавитном порядке. Вот начало списка:
1. ААААА
2. ААААО
3. ААААУ
4. АААОА
5. …
Найдите слово, которое стоит на 140-м месте от начала списка.
1. 00000
2. 00001
3. 00002
4. 00010
5. …
в троичной системе!
на 1-м месте: 0
на 140-м месте: 139
139 = 120113

ПРИМЕРЫ ЗАДАЧ
Все 5-буквенные слова, состоящие из букв А,О,У, записаны а алфавитном порядке. Вот начало списка:
ААААА
ААААО
ААААУ
АААОУ
Выполните следующие задания:
А) определите, сколько всего слов в списке;
Б) укажите слова, которые стоят на 101-м, 125-м, 170-м и 210-м местах
В) укажите порядковые номера слов ОАОАО, УАУАУ, АОУОА, УОАОУ
Г) укажите номер первого и последнего слова, которое начинается с буквы О

ПРИМЕРЫ ЗАДАЧ
Все 5-буквенные слова, состоящие из букв А,К,Р, У, записаны а алфавитном порядке. Вот начало списка:
ААААА
ААААК
ААААР
ААААУ
АААКА
Выполните следующие задания:
А) определите, сколько всего слов в списке;
Б) укажите слова, которые стоят на 150-м, 250-м, 350-м и 450-м местах
В) укажите порядковые номера слов АКУРА, КАРАУ, РУКАА, УКАРА, УРАКА
Г) укажите номер первого и последнего слова, которое начинается с буквы Р

ДРОБНЫЕ ЧИСЛА
0,6375 = 6·0,1 + 3·0,01 + 7·0,001 + 5·0,0001
0, 6 3 7 5 = 6·10-1 + 3·10-2 + 7·10-3 + 5·10-4
Развёрнутая форма записи:
разряды: -1 -2 -3 -4
Схема Горнера:
0, 6375 = 10-1·(6 + 10-1·(3 + 10-1·(7 + 10-1·5)))
0, 1 2 3 45 = 1·5-1 + 2·5-2 + 3·5-3 + 4·5-4
0,12345 = 5-1·(1 + 5-1·(2 + 5-1·(3 + 5-1·4)))
перевод в десятичную систему
перевод в десятичную систему

ДРОБНЫЕ ЧИСЛА: ИЗ ДЕСЯТИЧНОЙ В ЛЮБУЮ
0,12345 = 5-1·(1 + 5-1·(2 + 5-1·(3 + 5-1·4)))
5·(0,12345)= 1 + 5-1·(2 + 5-1·(3 + 5-1·4))
целая часть
дробная часть
0,a1a2a3a4 = p-1⋅(a1 + p-1⋅(a2 + p-1⋅(a1 + p-1⋅ a0)))
p⋅(0,a1a2a3a4) = a1 + p-1⋅(a2 + p-1⋅(a1 + p-1⋅ a0))

ДРОБНЫЕ ЧИСЛА: ИЗ ДЕСЯТИЧНОЙ В ЛЮБУЮ
10 → 5
0,9376
0,9376 = 0,43215

АЛГОРИТМ ПЕРЕВОДА ДРОБНОЙ ЧАСТИ ВЕЩЕСТВЕННОГО ЧИСЛА
Дробную часть числа (M) умножить на основание p.
Записать целую часть полученного числа в позицию с номером -1;
Выделить дробную часть получившегося числа и умножить на p;
Выделить целую часть числа и записать ее в следующей справа разряд дробной части.
Выполнять пункты 3-4 до тех пор, пока в дробной части не будет получен ноль или не будет достигнута требуемая точность, например пять знаков после запятой
Заметим, что при переводе числа из десятичной системы счисления в другую систему может получиться число с бесконечной дробной частью

ДРОБНЫЕ ЧИСЛА: ИЗ ДЕСЯТИЧНОЙ В ЛЮБУЮ
10 → 5
0,3
10 → 6
25,375
10 → 7
0,311
10 → 3
215,305

ПРИМЕРЫ ЗАДАЧ
Запишите число 0,123214 в развернутой форме и с помощью схемы Горнера
Перевидите число 15,125 в двоичную, четверичную, шестеричную и восьмеричную системы
Какие из этих чисел больше 0,5; 0,0112;0,123;0,214; 0,225; 0,256;0,357;0,358?
Переведите числа 11,125; 15,75; 22,6875 и 30,375 в систему счисления с основанием 4

ДОМАШНЕЕ ЗАДАНИЕ
Переведите из римской системы счисления: MDCXLIX, MMCDLXIV, CDXCI
Переведите в римскую систему счисления 103,2067, 1951,2019
Переведите в десятичную систему счисления: F2B416,101001102,20120113, 6578
Известно, что для целого числа x выполнено: 334+х-334=3310.Определите значение х. Ответ запишите в десятичной системе счисления.
Запись числа 67 в системе счисления с основанием N оканчивается на 1 и содержит 4 цифры. Укажите основание N этой системы счисления