Системы счисления: продолжение

Представление действительных чисел
Если в дробной части числа конечное число знаков k, то нижний
индекс суммы равен —к .
0.375=(3+(7+5/10)/10)/10=(3+(7+(5+0)/10)/10)/10
S =

Связь дробной части числа со значением
где i = k, … , 1;

Примеры
N(«1.101(2)») = 1⋅20 +1⋅2-1 +0⋅2-2 +1⋅2-3
= 1 + 0.5 + 0.125
= 1.625
Nf(«1.101(2)») =(1 +(0 +(1 +0)/2)/2)/2
= (1 + (0 + 0.5)/2 )/2
= (1 + 0.25) / 2 = 0.625
Nf(«0.01(3)») = 1⋅3-2 = = 0.(1)

Целая часть числа Nf*b (0 < Nf < 1) равна первой цифре дробной части числа Nf
Алгоритм А4: перевод дробной части из 10-с. с. в b-с.с
Вход: Nf ( 0 ≤ Nf < 1), b >1;
i := -1;
цикл
([x]-взятие целой части числа)
( остается в том же диапазоне )
i := i – 1;
пока
k := i;
Выход: набор (число значащих цифр).
Алгоритм А4 может не завершиться, если данное число не представимо конечной дробью в b-с.с
Требуется k умножений (выражение Nf*b можно вычислять в цикле один раз и
хранить в промежуточной переменной).

Пример:

Теорема Т2
Несократимая дробь p/q конечно представима в системе счисления с основанием b в том и только в том случае, когда все числа из разложения q на простые множители входят в такое же разложение b (количество повторений не учитывается).
Пример
121/675 конечна в 15-с.с.:
675 = 33*52; 15 = 3*5;
1/675 = 5*15-3 = 0.005(15);
121*5/15-3 = (2*152 + 10*151 + 5)/15-3 = 2/15-1 + 10/15-2 + 5/15-3
121/675 = 0.2A5(15);
1/10 бесконечна в 2-с.с. !!!!

Алгоритм А5:
(перевод дробной части из b-с.с. в 10-с.с)
Вход: b > 1, к > 0 (число дробных цифр), набор
(S накапливает степень, — значение )
цикл по i от -1 вниз до -k
;
конец цикла
Выход:
2k операций *, /
k операций +

Алгоритм А6:
перевод дробной части из b-с.с. в 10-с.с.
( из формулы (7) по схеме Горнера)
Вход: b >1, k > 0 (число цифр), набор
цикл по i от –k до -1
конец цикла;
Выход:
k операций + и /

Число N в b-с.с. имеющее k дробных цифр, при умножении на bk становится целым (это умножение соответствует сдвигу точки на k позиций вправо)
Алгоритм А7
• найти целое N1 = N * b1k (умножением или сдвигом точки);
• выполнить для N1 один из алгоритмов А1 или А2, затем АЗ;
• разделить полученный результат на b1k в системе b2

Пример
Перевести 101.101(2) в 10-с.с.
1) умножим на 23 → 101101(2)
2) переведем в 10-с.с. → 45
3) разделим: 45/8 = 5.625(10)
101.101=1*22+1*20+1*2-1+1*2-3=5+1/2+1/8=5.625

Кратные системы счисления
Если основания двух систем счисления b1 и b2 связаны соотношением b2= b1m для некоторого натурального т, то такие системы счисления называются кратными.
Перевод числа из одной с. с. в другую для таких систем можно выполнить проще.
Сгруппируем цифры в b1-записи числа по m от точки влево и вправо (добавив при нехватке цифр нужное количество незначащих нулей):

затем также сгруппируем слагаемые в формуле (5) (они содержат множитель b1 в степени, равной индексу цифры), вынесем за скобки из каждой группы i общий множитель
(b1im = (b1m)i = b2i)
и обозначим для каждой группы
Тогда значение исходного числа может быть представлено в виде:
N(S’) = Ak’* b2k’ + … + Ai* b2i + ... + А0*b20 + А-1*b2-1+ … А-j b2-j,
что по определению совпадает со значением записи того же числа в b2-с.c. c цифрами Аi, если заметить, что Аi, действительно могут принимать все значения от 0 до b1m − 1 = b2 − 1.

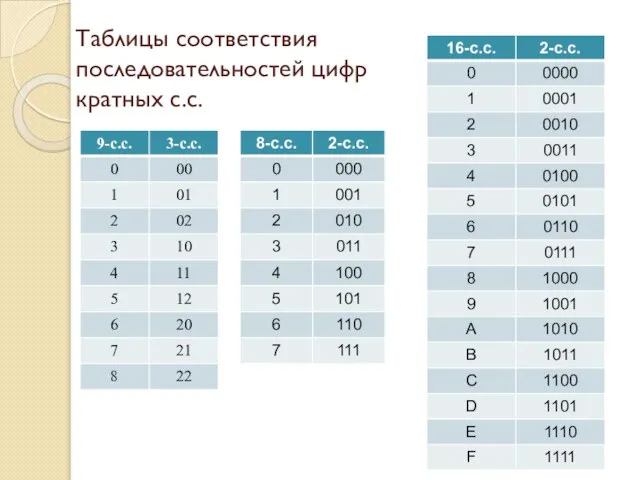
Таблицы соответствия
последовательностей цифр кратных с.с.

Алгоритм А8: перевод из меньшей кратной с.с. в большую
Вход: b1 > 1, b2 = b1m, b1 - представление числа;
• разбить число на группы по т цифр, начиная от точки, в обе стороны (если в крайних группах цифр меньше т, добавить незначащие нули: в целой части спереди, в дробной сзади);
• заменить каждую группу b2-цифрой по формуле (8) или таблице.
Выход: b2 -представление исходного числа.

Алгоритм А9: перевод из большей кратной с.с. в меньшую
Вход: b1> 1, b2= b1m; b2-представление числа;
заменить каждую b2-цифру цепочкой из т b1-цифр по формуле (8) или таблице;
отбросить незначащие нули слева и справа.
Выход: b1-представление исходного числа.

Универсальные алгоритмы для арифметических операций
Все так называемые численные алгоритмы для арифметических операций сложения, вычитания, умножения и деления (в том числе, вычисления «столбиком») являются символьными, потому что оперируют входными, выходными и промежуточными данными как строками символов.
Символьные вычисления являются формальными в том смысле, что манипулируют только знаками, не обращаясь к их значениям.
Абстрагирование от смысла данных различной природы и описание алгоритма в терминах чисто символьных преобразований является одним из основных методов программирования обработки данных произвольной природы

Алгоритм А10: сложение двух чисел
Вход: две строки цифр, представляющие слагаемые;
• выравнивание: расположить слагаемые одно под другим в произвольном порядке так, чтобы разряды с одинаковым весом находились друг под другом; если какое-то число короче других слева или справа, дополнить его нулями;
• начальные установки:
обнулить цифру переноса в следующий разряд;
установить результат равным пустой строке;
• цикл по текущему разряду от младшего до старшего:
определить сумму переноса и цифр в столбце текущего разряда чисел; младшую цифру суммы записать в текущий разряд результата, старшую — в перенос;
конец цикла;
• окончание: если перенос не равен 0, то дописать перенос в начало результата
Выход: строка, представляющая результат.

Единственное место в этом алгоритме, где присутствует
обращение к значениям цифровых символов, — это поразрядное сложение в цикле.
Действительно, из одного лишь вида знаков «2» и «3» нельзя извлечь информацию, что результатом их сложения будет знак «5».
Эти сведения можно задать, например, двумя таблицами сложения: в одной для каждой пары цифр записать младшую цифру результата, в другой — цифру переноса («0» или «1»);
исчерпав таким образом все немногочисленные случаи, можно заменить операцию сложения значений операцией выборки знака из таблицы.
Чтобы учесть сложение с переносом, можно завести две пары
таблиц или записать в каждую клетку по две цифры.

Алгоритм А10 замечателен тем, что применим к произвольной позиционной с. с. при соответствующей замене таблиц сложения.