Р. 4. Портфельный анализ

Две проблемы выбора инвестора:
В какие активы из имеющихся и в каких пропорциях вкладывать средства?
2. На практике более высокий уровень доходности связан с более высоким риском. Поэтому инвестор может выбрать актив с высокой доходностью и большим риском или с гарантированной низкой доходностью и с меньшим риском.

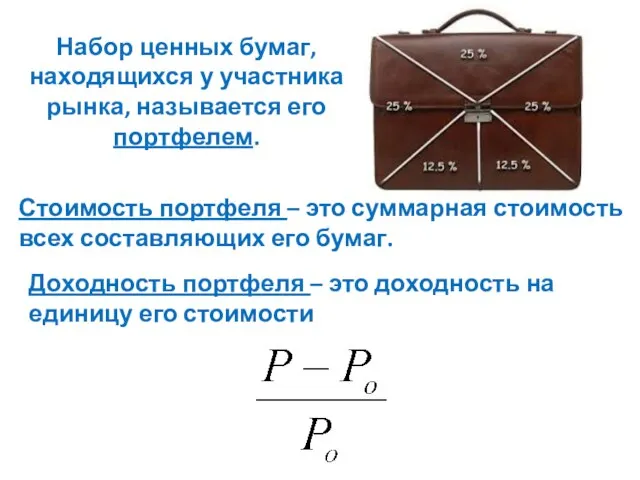
Набор ценных бумаг, находящихся у участника рынка, называется его портфелем.
Стоимость портфеля – это суммарная стоимость всех составляющих его бумаг.
Доходность портфеля – это доходность на единицу его стоимости

С каждым портфелем Х связаны две величины:
1) эффективность (ожидаемая доходность)
2) риск
Величина называется ковариацией доходностей ценных бумаг i-го и j-го видов и характеризует степень их взаимной изменчивости (связи).

4.2. Портфель из двух бумаг
Дисперсия портфеля из двух бумаг
Риск
Доходность

В случае полной корреляции

В случае полной антикорреляции
При полной антикорреляции возможен портфель нулевого риска

Для независимых бумаг
Найдем портфель минимального риска и его доходность и риск

Модель задачи нелинейного программирования
Решение задачи дает портфель
Его доходность
Его риск
Принцип диверсификации: при «размазывании» портфеля по независимым бумагам его риск уменьшается

Для случая трех независимых бумаг
Портфель
Доходность
Риск
Для решения поставленной задачи можно использовать надстройку Excel «Поиск решений»

Безрисковая бумага
Допустимое множество портфелей
Допустимое множество портфелей представлено отрезком [1,2].

Портфель заданной эффективности
Портфель однозначно находится как решение системы
Портфель заданного риска
Находится как решение системы

4.3. Портфели из n–бумаг. Портфели Марковица
Задача: требуется найти портфель, который минимизировал бы риск и обеспечивал заданную величину ожидаемой доходности.
На практике для решения поставленной задачи можно использовать надстройку Excel «Поиск решений», которая применяется как для решения задач линейного, так и для решения задач нелинейного программирования, каковой является поставленная задача

Для каждого значения ожидаемой доходности имеется единственный портфель Х, обеспечивающий минимальное значение риска , т.е. определена функция
График этой функции называют минимальной границей
Кривая МВ, которая называется эффективной границей

4.4. Портфели Тобина
Портфель Тобина – это портфель Марковица при наличии на рынке безрисковых ценных бумаг
Обычно предполагают, что ожидаемая доходность портфеля должна быть не меньше доходности безрискового актива

Минимальная граница риска для портфеля Тобина превращается в прямую, касательную к графику минимальной границы
Всякий минимальный портфель является линейной комбинацией безрискового актива и рисковой части, лежащей на минимальной границе. Поэтому всякая такая точка лежит на луче FA, где точка F соответствует безрисковому активу. Из точки А можно переместиться вдоль горизонтальной оси в точку В, лежащую на касательной FT, у которой риск тот же, а доходность выше. Поэтому касательная FT является искомой минимальной границей.

4.5. Диверсификация портфеля
Диверсификация в области финансов – это распределение инвестиций по разным финансовым инструментам.
Диверсификация инвестиционного портфеля – это распределение средств между различными объектами инвестирования с целью избежания серьезных потерь в случае падения цен одного или нескольких активов инвестиционного портфеля.