Содержание
- 2. Математическая логика § 5. Логика и компьютер
- 3. Логика, высказывания Логика (др.греч. λογικος) – это наука о том, как правильно рассуждать, делать выводы, доказывать
- 4. Высказывание или нет? Сейчас идет дождь. Жирафы летят на север. История – интересный предмет. У квадрата
- 5. Логика и компьютер Логика изучает операции между 0 и 1! Джордж Буль Алгебра логики — это
- 6. Простые и составные высказывания A – Сейчас идет дождь. B – Форточка открыта. простые высказывания (элементарные)
- 7. Операция НЕ (инверсия) Если высказывание A истинно, то «не А» ложно, и наоборот. 1 0 0
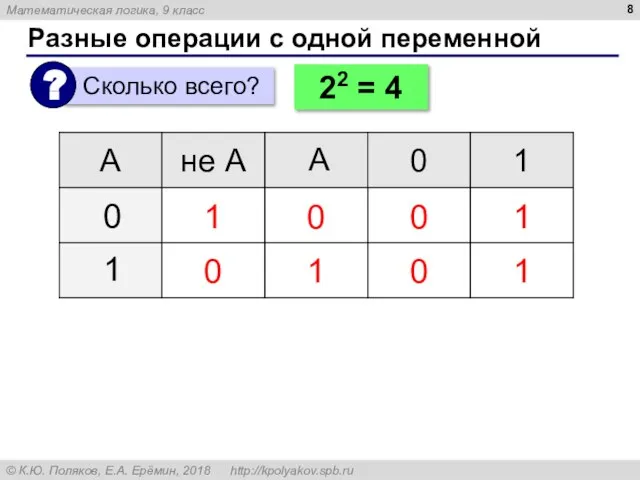
- 8. Разные операции с одной переменной 1 0 0 1 1 0 А 0 0 1 1
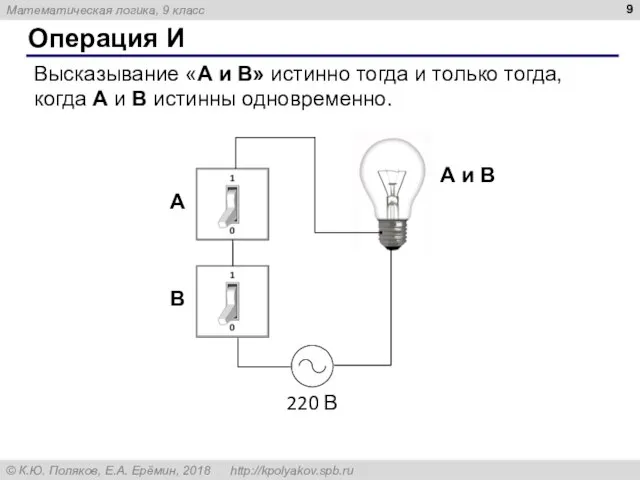
- 9. Операция И Высказывание «A и B» истинно тогда и только тогда, когда А и B истинны
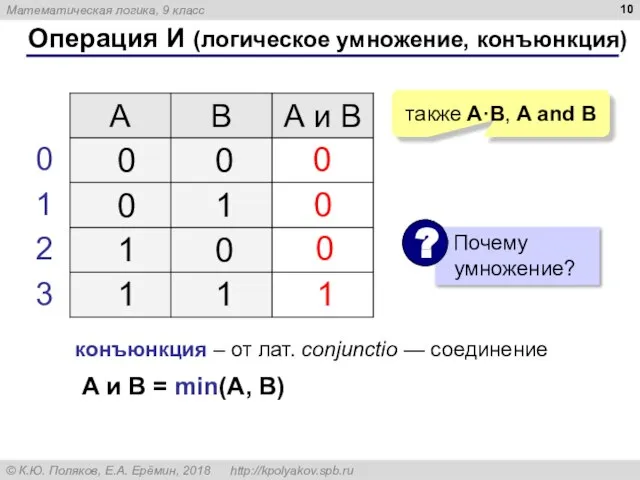
- 10. Операция И (логическое умножение, конъюнкция) 1 0 также A·B, A and B 0 0 конъюнкция –
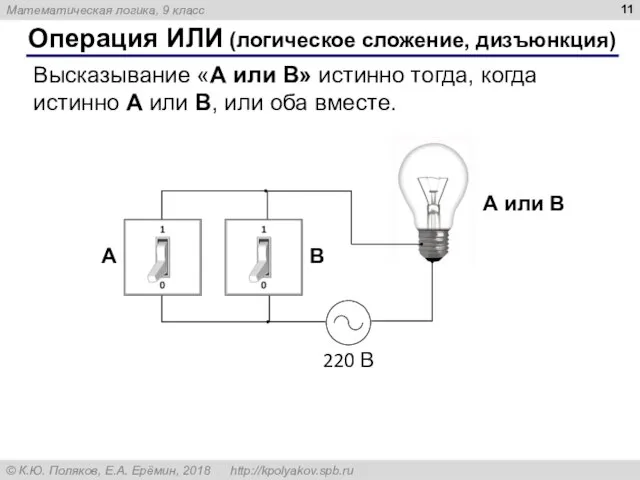
- 11. Операция ИЛИ (логическое сложение, дизъюнкция) Высказывание «A или B» истинно тогда, когда истинно А или B,
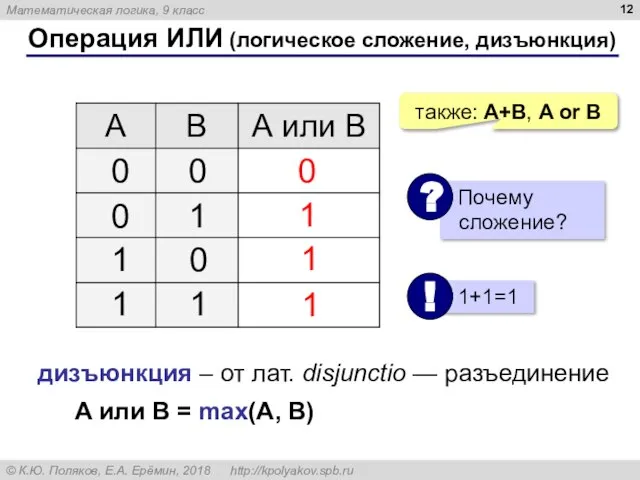
- 12. Операция ИЛИ (логическое сложение, дизъюнкция) 1 0 также: A+B, A or B 1 1 дизъюнкция –
- 13. Упрощение логических выражений A и 0 = A ∙ 0 = A и 1 = A
- 14. Математическая логика § 6. Логические элементы
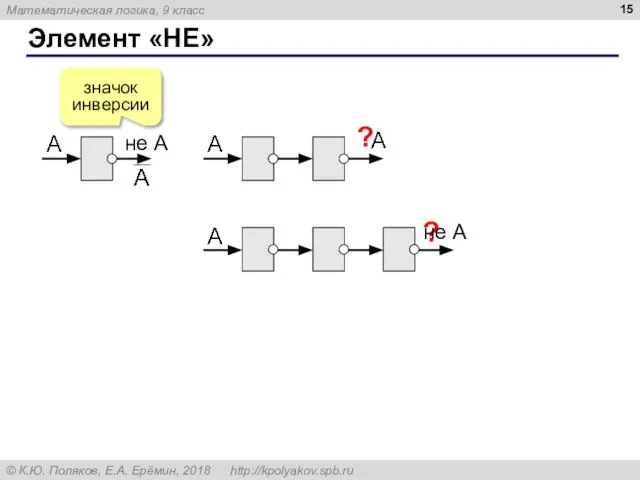
- 15. Элемент «НЕ» значок инверсии ? ? не A не A
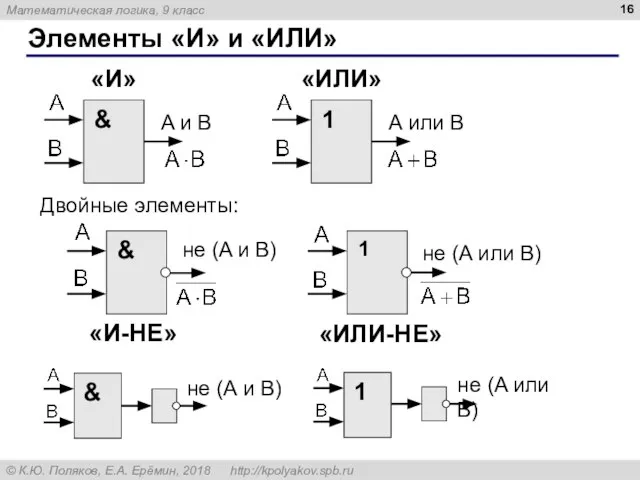
- 16. Элементы «И» и «ИЛИ» A и B A или B Двойные элементы: «ИЛИ-НЕ» «И-НЕ» не (A
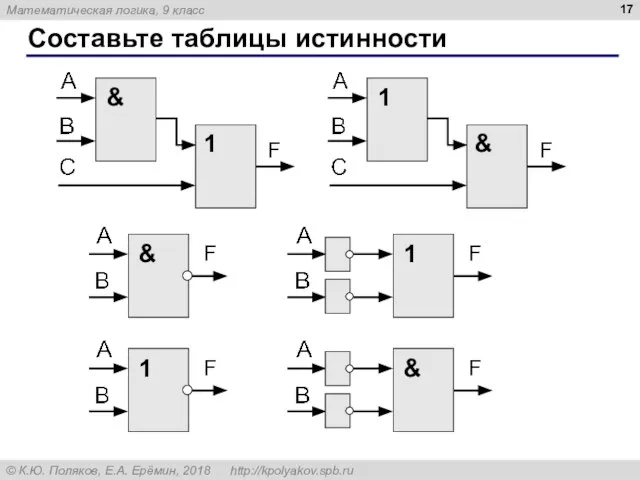
- 17. Составьте таблицы истинности
- 18. Математическая логика § 7. Другие логические операции
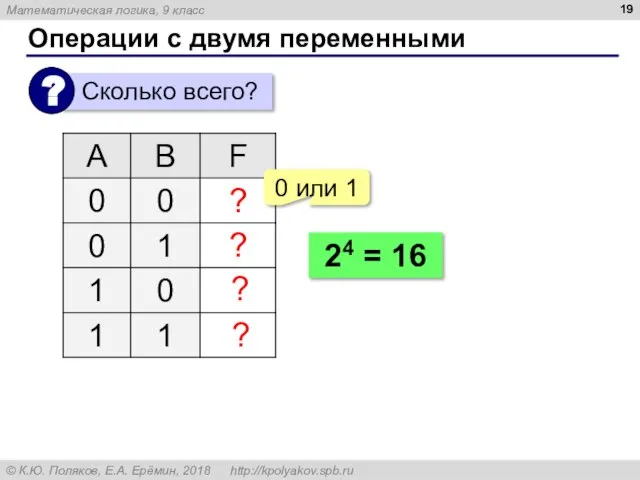
- 19. Операции с двумя переменными ? ? ? ? 0 или 1 24 = 16
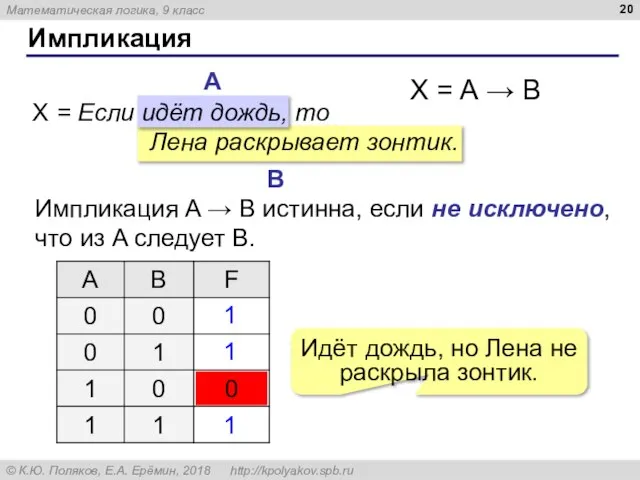
- 20. Импликация X = Если идёт дождь, то Лена раскрывает зонтик. X = A → B Импликация
- 21. Постройте таблицы истинности B → A ≠ A → B X = B → A
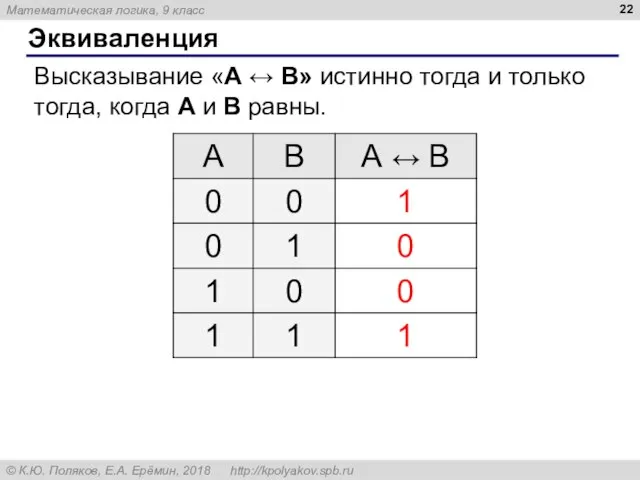
- 22. Эквиваленция Высказывание «A ↔ B» истинно тогда и только тогда, когда А и B равны.
- 23. Постройте таблицы истинности
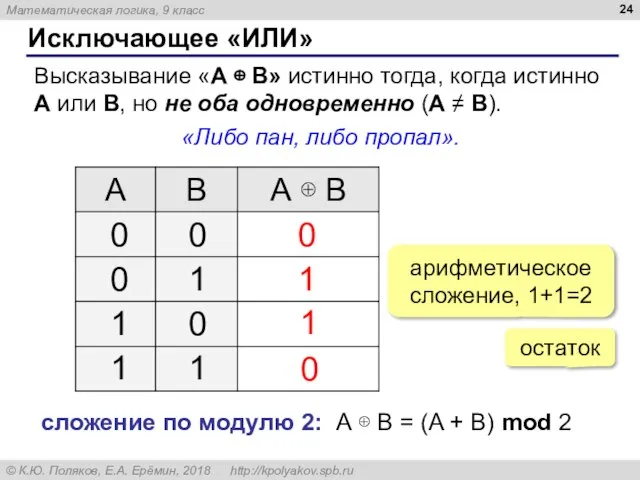
- 24. Исключающее «ИЛИ» Высказывание «A ⊕ B» истинно тогда, когда истинно А или B, но не оба
- 25. Постройте таблицы истинности
- 26. Упрощение логических выражений A ⊕ 0 = A ⊕ 1 = A ⊕ A = (A
- 27. Шифрование (A ⊕ B) ⊕ B = A данные шифровка дешифровка A = 1 0 0
- 28. Математическая логика § 8. Логические выражения
- 29. Логические выражения Логическое выражение — это выражение, результат вычисления которого — логическое значение (истина или ложь).
- 30. Порядок вычисления скобки НЕ И ИЛИ импликация эквиваленция 1 2 3 4 5 6 , исключающее
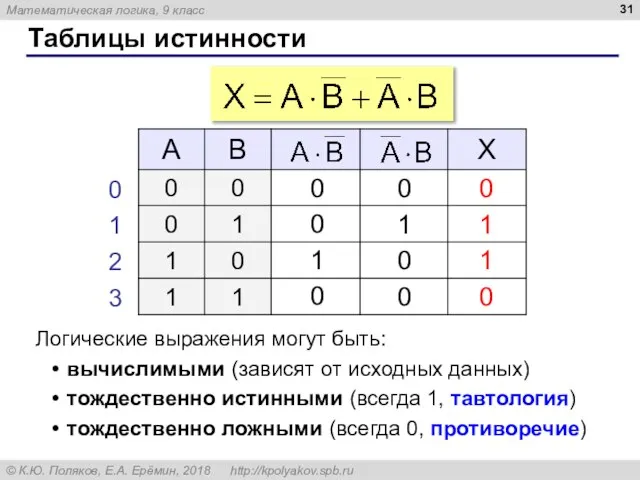
- 31. Таблицы истинности Логические выражения могут быть: вычислимыми (зависят от исходных данных) тождественно истинными (всегда 1, тавтология)
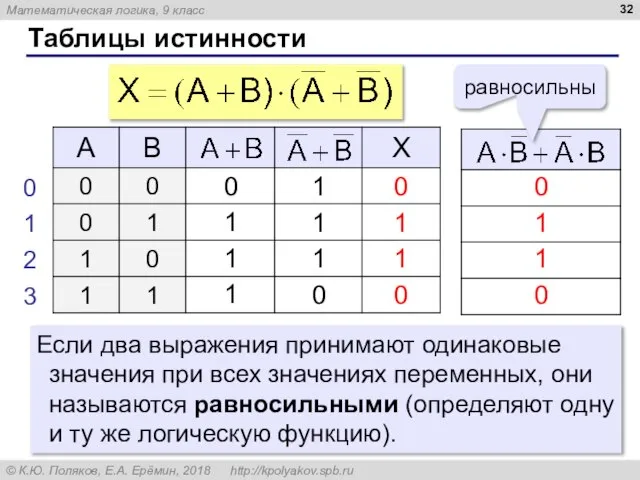
- 32. Таблицы истинности Если два выражения принимают одинаковые значения при всех значениях переменных, они называются равносильными (определяют
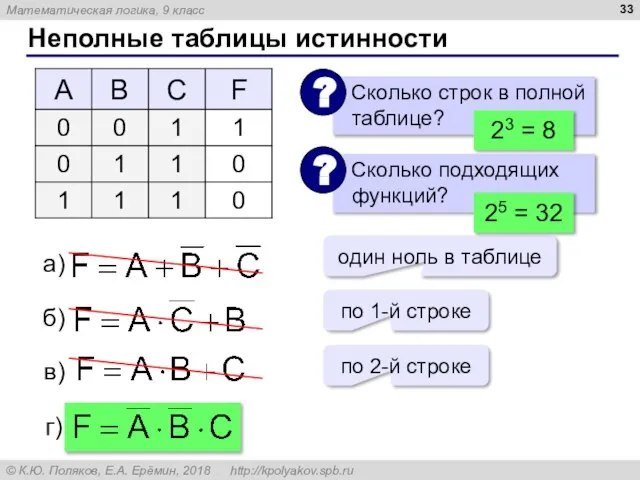
- 33. Неполные таблицы истинности 23 = 8 один ноль в таблице по 1-й строке по 2-й строке
- 34. Сколько нулей и единиц? в таблице истинности функции от 3-х переменных: 1 7 7 1 7
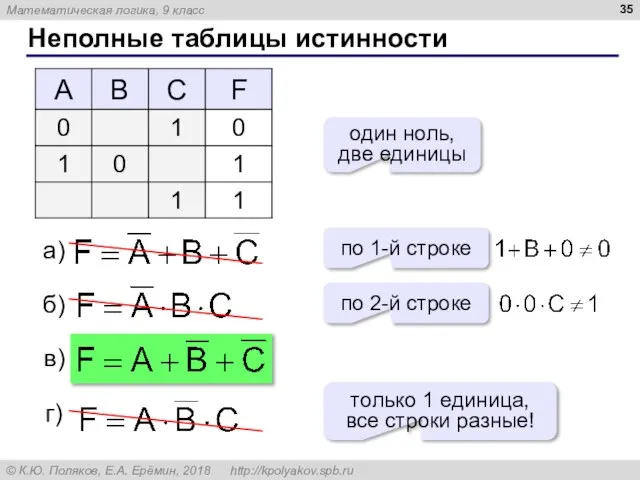
- 35. Неполные таблицы истинности один ноль, две единицы по 1-й строке по 2-й строке только 1 единица,
- 36. Составление условий (x ≥ 3) и (x ≤ 6) (3 ≤ x) и (x ≤ 6)
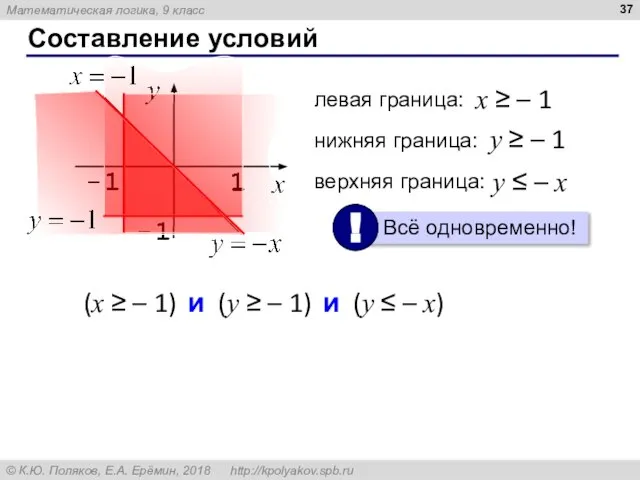
- 37. Составление условий левая граница: x ≥ – 1 нижняя граница: y ≥ – 1 верхняя граница:
- 38. Составление условий (x2+y2 ≤ 1) и (x ≤ 0) левая правая (x ≥ 0) и (x2+y2
- 39. Составление условий = + ((x2+y2 ≤ 1) и (x ≤ 0)) или ((x2+y2 ≤ 1) и
- 40. Определение истинности выражений Для каких из указанных значений числа X истинно высказывание: (X X = 2:
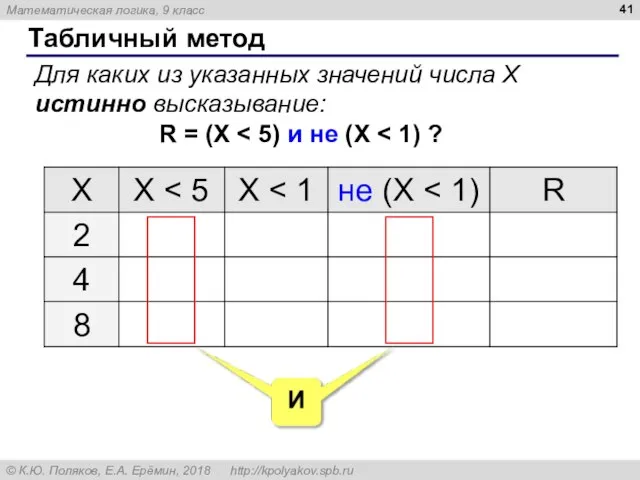
- 41. Табличный метод Для каких из указанных значений числа X истинно высказывание: R = (X
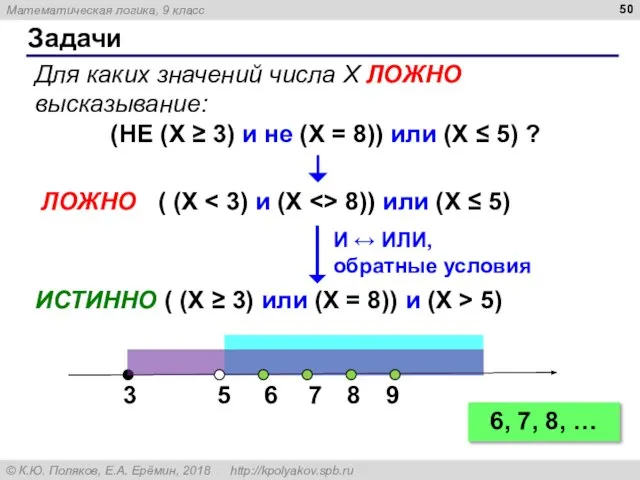
- 42. Задачи Для каких из указанных значений числа X ЛОЖНО высказывание: (не (X ≥ 3) и не
- 43. Задачи Для каких значений числа X истинно высказывание: (X (X = 1) 1, 2, 3, 4
- 44. Задачи Для каких из приведённых имён ЛОЖНО высказывание: НЕ(Первая буква гласная) или (Последняя буква гласная) ?
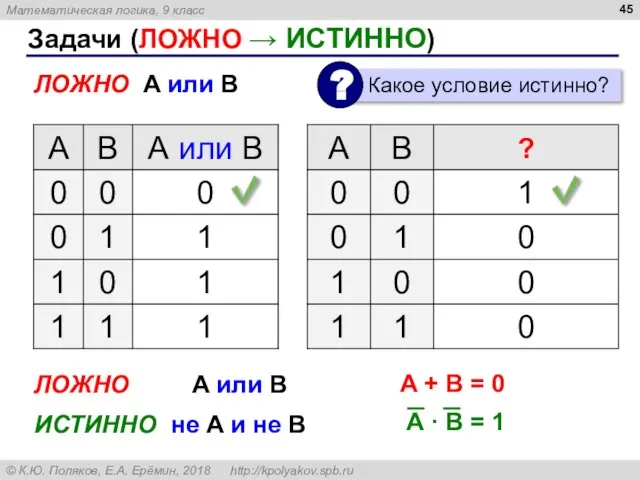
- 45. Задачи (ЛОЖНО → ИСТИННО) ЛОЖНО A или B ЛОЖНО A или B ИСТИННО не A и
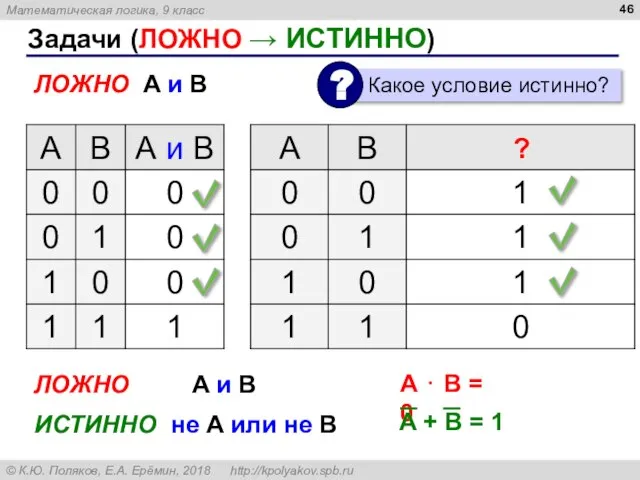
- 46. Задачи (ЛОЖНО → ИСТИННО) ЛОЖНО A и B ЛОЖНО A и B ИСТИННО не A или
- 47. Задачи (ЛОЖНО → ИСТИННО)
- 48. Задачи Для каких из приведённых имён ЛОЖНО высказывание: НЕ(Первая буква гласная) или (Последняя буква гласная) ?
- 49. Задачи Для каких из приведённых имён ЛОЖНО высказывание: НЕ(Первая буква гласная) и (Последняя буква гласная) ?
- 50. Задачи Для каких значений числа X ЛОЖНО высказывание: (НЕ (X ≥ 3) и не (X =
- 51. Задачи Напишите наибольшее число x, для которого истинно высказывание: (x (x 33
- 52. Задачи Напишите наименьшее число x, для которого ЛОЖНО высказывание: (x (x ≥ 42) и (x не
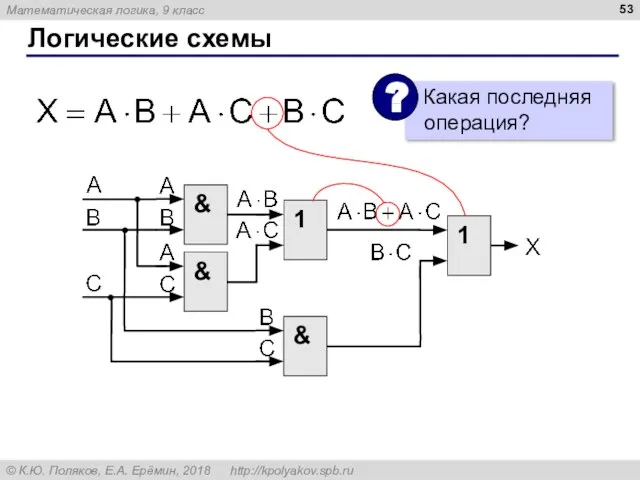
- 53. Логические схемы
- 54. Математическая логика § 12. Множества и логика
- 55. Что такое множество? Множество – некоторый набор элементов, каждый из которых отличается от остальных. пустое множество:
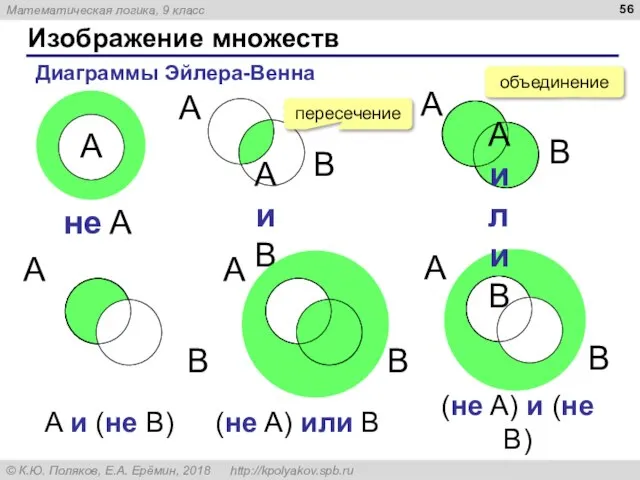
- 56. Изображение множеств Диаграммы Эйлера-Венна A и B A или B (не A) или B пересечение объединение
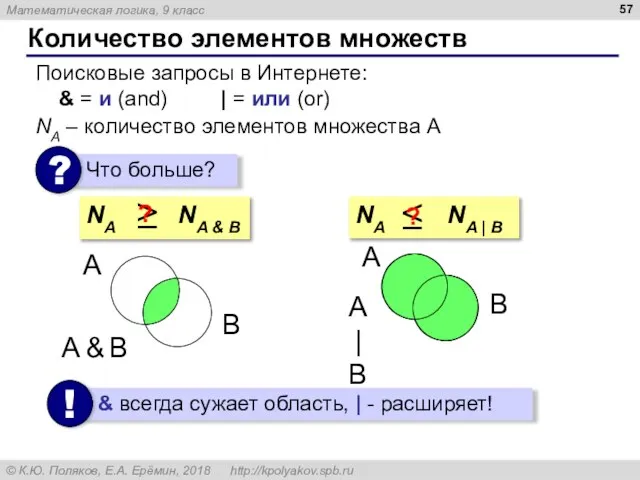
- 57. Количество элементов множеств Поисковые запросы в Интернете: & = и (and) | = или (or) NA
- 58. Задачи В таблице приведены запросы к поисковому серверу. Расположите номера запросов в порядке возрастания количества страниц,
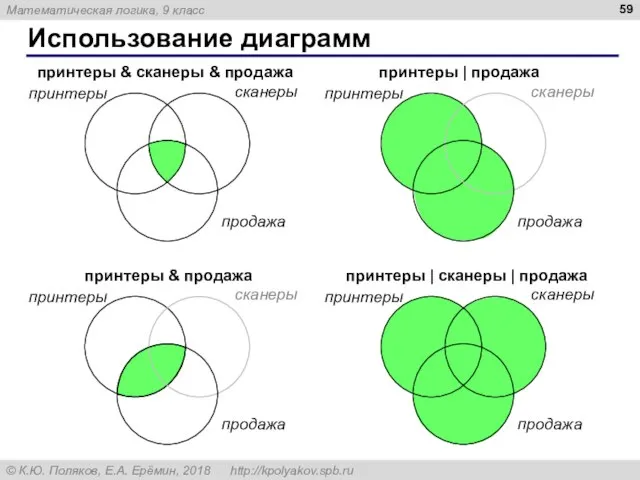
- 59. Использование диаграмм принтеры сканеры продажа принтеры & сканеры & продажа
- 60. Задачи В таблице приведены запросы к поисковому серверу. Расположите номера запросов в порядке убывания количества страниц,
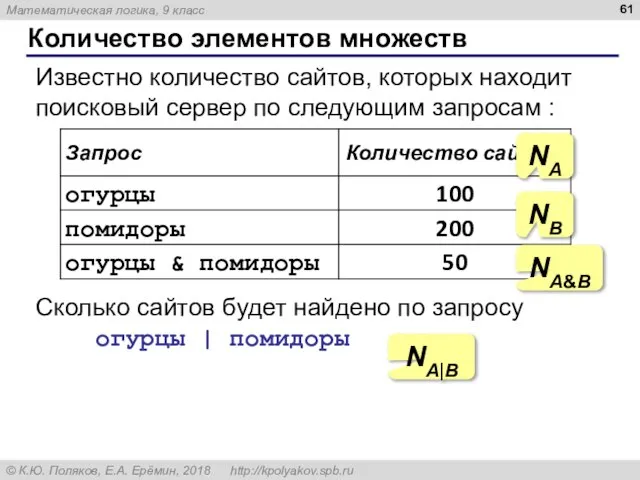
- 61. Количество элементов множеств Известно количество сайтов, которых находит поисковый сервер по следующим запросам : Сколько сайтов
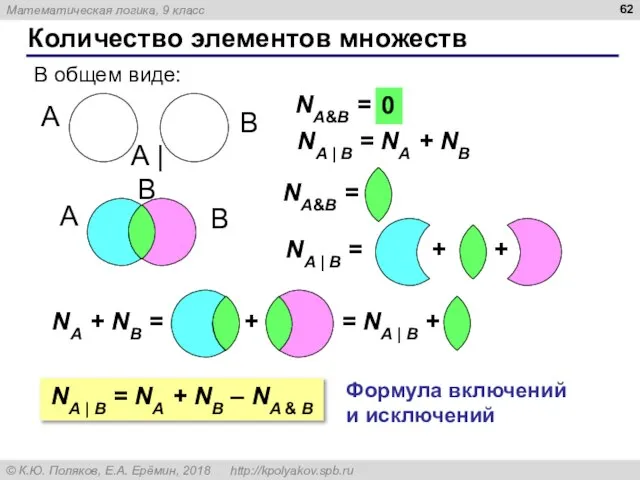
- 62. Количество элементов множеств A B В общем виде: NA&B = ? 0 NA | B =
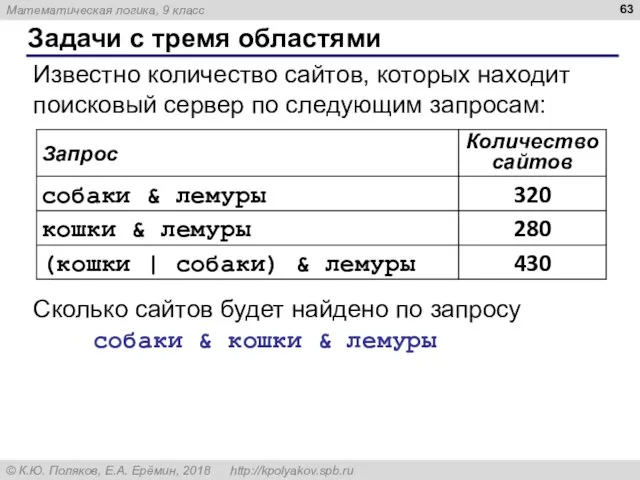
- 63. Задачи с тремя областями Известно количество сайтов, которых находит поисковый сервер по следующим запросам: Сколько сайтов
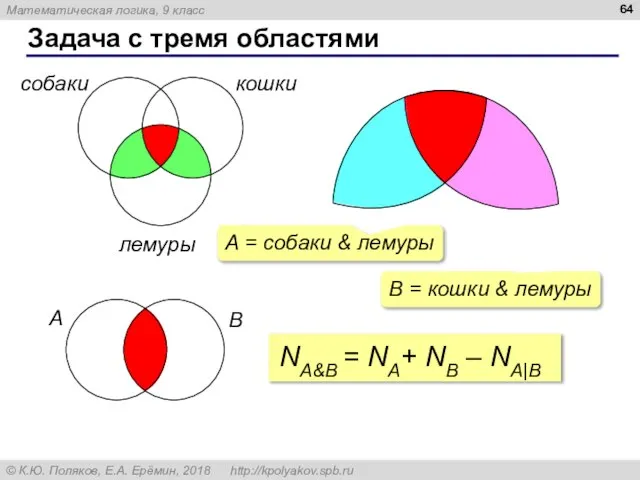
- 64. Задача с тремя областями собаки кошки лемуры B = кошки & лемуры A B NA&B =
- 65. Задачи с тремя областями Известно количество сайтов, которых находит поисковый сервер по следующим запросам: Сколько сайтов
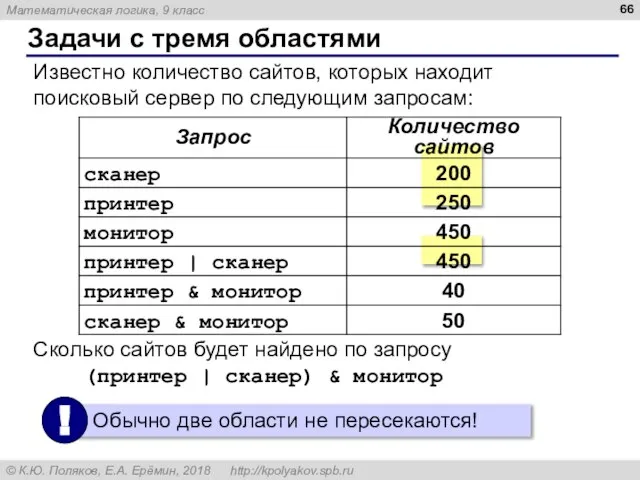
- 66. Известно количество сайтов, которых находит поисковый сервер по следующим запросам: Сколько сайтов будет найдено по запросу
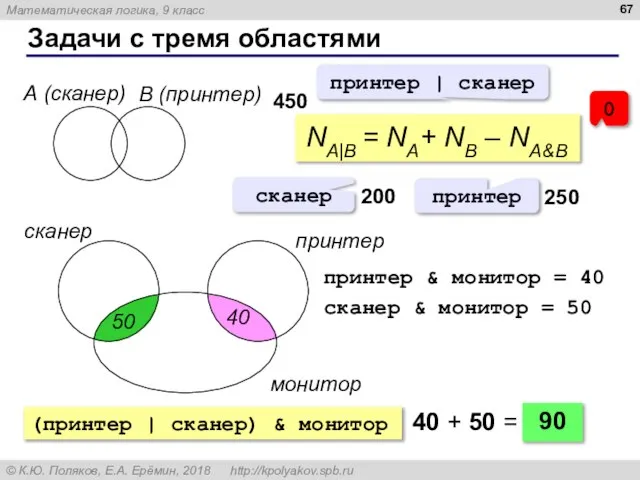
- 67. Задачи с тремя областями А (сканер) B (принтер) NA|B = NA+ NB – NA&B принтер |
- 68. Конец фильма ПОЛЯКОВ Константин Юрьевич д.т.н., учитель информатики ГБОУ СОШ № 163, г. Санкт-Петербург [email protected] ЕРЕМИН
- 70. Скачать презентацию




































 Состав компьютера
Состав компьютера Управление звуком от таймера, генерация тона
Управление звуком от таймера, генерация тона Одобрение Онлайн по объектам на ДомКлик
Одобрение Онлайн по объектам на ДомКлик Конфігурація комп’ютера
Конфігурація комп’ютера HMI Screen 01
HMI Screen 01 Внеклассное мероприятие по информатике «Турнир знатоков компьютера» Учитель информатики МБОУ лицея с. Хлевное Чеканова Н.В.
Внеклассное мероприятие по информатике «Турнир знатоков компьютера» Учитель информатики МБОУ лицея с. Хлевное Чеканова Н.В. Алгоритмизация и требования к алгоритму
Алгоритмизация и требования к алгоритму ConnectKey 2017. Приложения и инструменты
ConnectKey 2017. Приложения и инструменты Доработка игры
Доработка игры Автоматизация схемы охраны и контроля образовательного учреждения
Автоматизация схемы охраны и контроля образовательного учреждения Варианты публикации вакансии на сайте
Варианты публикации вакансии на сайте Презентация на тему История Интернета и WEB
Презентация на тему История Интернета и WEB  Разработка виртуального тренажера обслуживания автоматизированной групповой замерной установки
Разработка виртуального тренажера обслуживания автоматизированной групповой замерной установки Data PowerPoint
Data PowerPoint Презентация - Комплексная система обеспечения информационной безопасности
Презентация - Комплексная система обеспечения информационной безопасности Мастер-класс. Создание поздравительной анимационной открытки
Мастер-класс. Создание поздравительной анимационной открытки Мордовия. Энергосбыт. Личный кабинет для юридических лиц
Мордовия. Энергосбыт. Личный кабинет для юридических лиц Разработка авторулевого для морских и речных судов
Разработка авторулевого для морских и речных судов Что умеет компьютер. О профессиях
Что умеет компьютер. О профессиях Электронная почта
Электронная почта Географические информационные системы
Географические информационные системы Коммуникационная стратегия Новосибирской области. Разработка рекомендаций по упрощению работы Интернет-портала
Коммуникационная стратегия Новосибирской области. Разработка рекомендаций по упрощению работы Интернет-портала PUG_МахровСемён_ИЭоз-61-22
PUG_МахровСемён_ИЭоз-61-22 Zakipki.Hack. Библиотека программиста
Zakipki.Hack. Библиотека программиста Что такое моделирование?
Что такое моделирование? Информационные технологии
Информационные технологии Универсальная битва полов
Универсальная битва полов Разработка инструмента для автоматизации процессов планирования и управления производственными ресурсами в авиастроении
Разработка инструмента для автоматизации процессов планирования и управления производственными ресурсами в авиастроении