Содержание
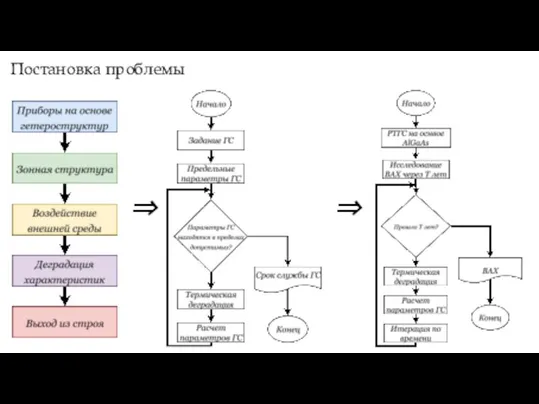
- 2. Постановка проблемы ⇒ ⇒
- 3. Цели и задачи Цель работы: ) Разработка алгоритма прогнозирования деградации слоистых гетероструктур на основе GaAs. Задачи
- 4. Численное моделирование физических процессов 0 S(x ) = 0 0 S(x ) d S(x + ∆x)
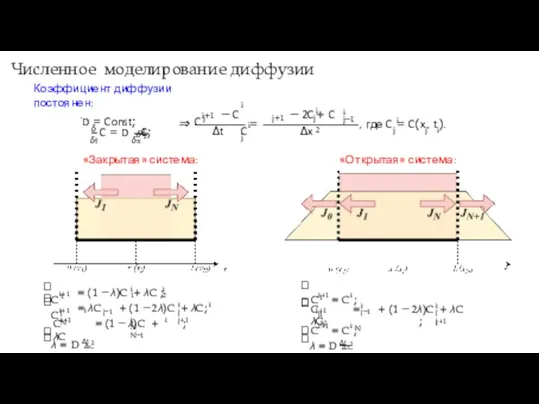
- 5. Численное моделирование диффузии Коэффициент диффузии постоянен: .D = Const; δ2 δ δt δx 2 C =
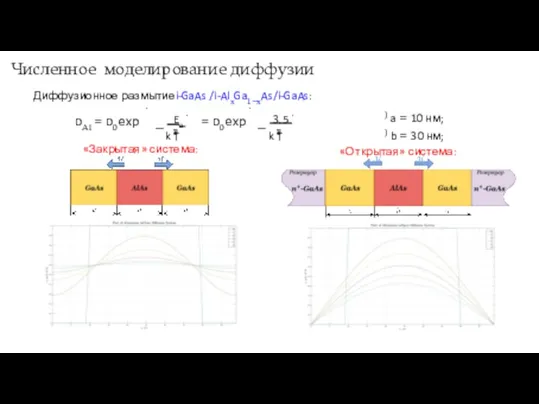
- 6. Численное моделирование диффузии Диффузионное размытиеi-GaAs /i-AlxGa1−xAs/i-GaAs: DAl = D0 exp . B − k T Ea
- 7. Численное моделирование диффузии Коэффициент диффузии зависит от концентрации: .D ƒ= Const; δ δ δ δt C
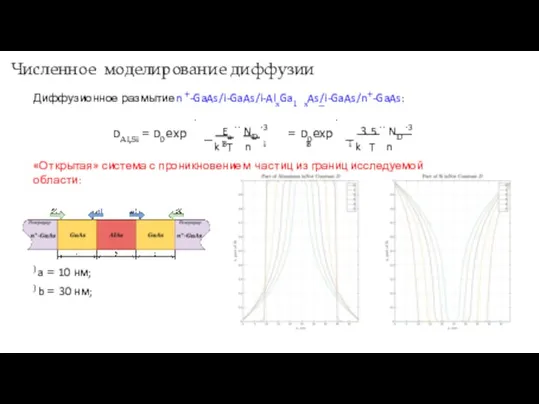
- 8. Численное моделирование диффузии Диффузионное размытиеn +-GaAs/i-GaAs/i-AlxGa1 xAs/i-GaAs/n+-GaAs: − DAl,Si = D0 exp . − k T
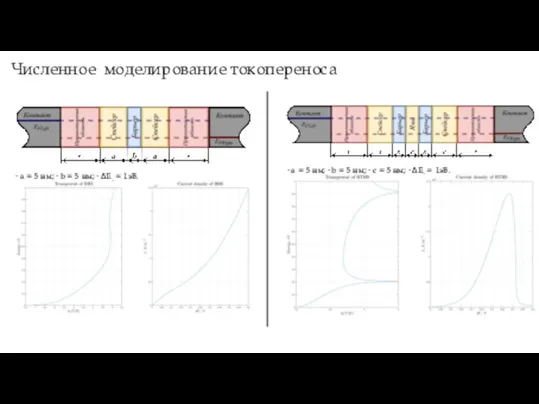
- 9. Численное моделирование токопереноса Формула Цу-Есаки: Численное решение уравнение Шредингера: J(V) = 2mekBT (2π)2k3 ¸∞ T(E)D(E)dE; 0
- 10. Численное моделирование токопереноса • a = 5 нм; • b = 5 нм; • ∆Ec =
- 11. Учет самосогласованного потенциала Уравнеие Пуассона: ε(x) Vs = d d e dx x ε0 [n(x) −
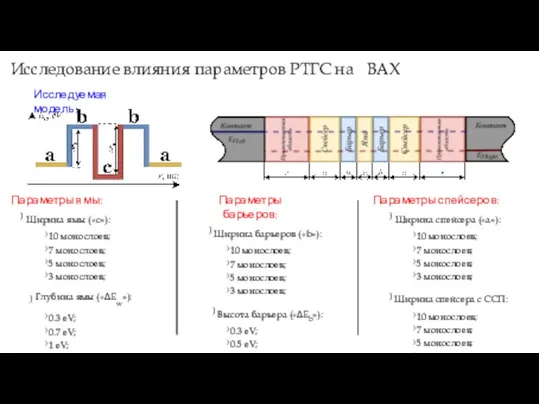
- 12. Исследование влияния параметров РТГС на ВАХ Исследуемая модель: Параметры ямы: ) Ширина ямы («c»): ) 10
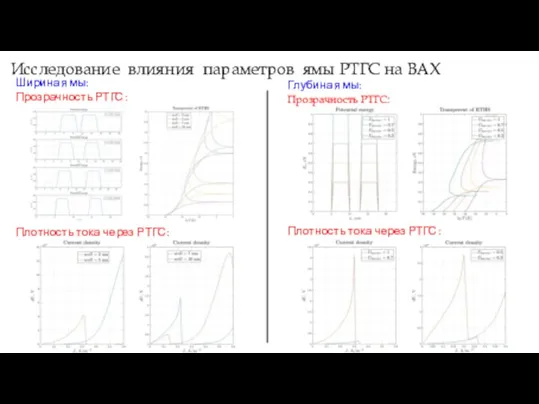
- 13. Исследование влияния параметров ямы РТГС на ВАХ Ширина ямы: Прозрачность РТГС: Плотность тока через РТГС: Глубина
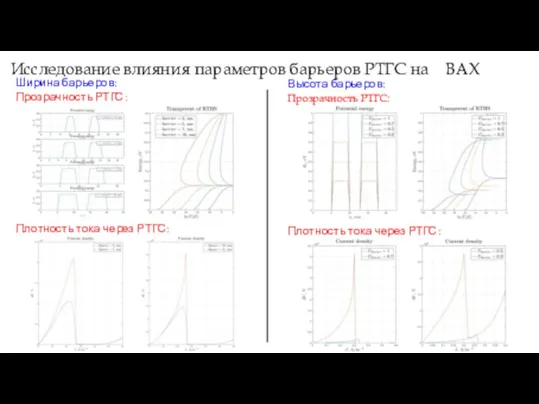
- 14. Исследование влияния параметров барьеров РТГС на ВАХ Ширина барьеров: Прозрачность РТГС: Плотность тока через РТГС: Высота
- 15. Исследование влияния параметров спейсера РТГС на ВАХ Ширина спейсера: Прозрачность РТГС: Плотность тока через РТГС: Ширина
- 16. Моделирование термической деградации ВАХ AlxGa1−xAs РТГС Исследуемая модель: Схема: Зонная структура: AlxGa1−xAs: EΓ g = Период
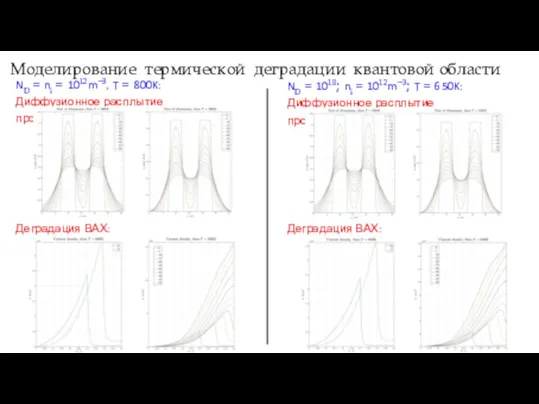
- 17. Моделирование термической деградации квантовой области ND = ni = 1012m−3, T = 800K: Диффузионное расплытие профиля:
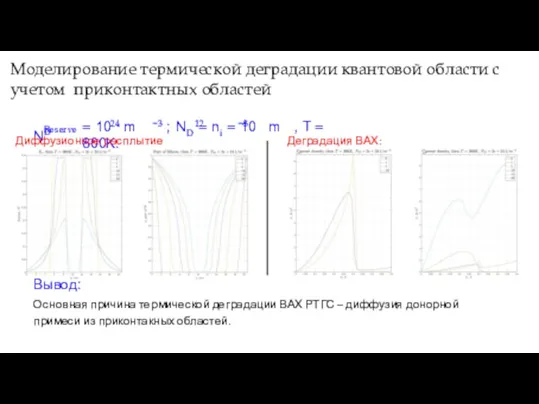
- 18. Моделирование термической деградации квантовой области с учетом приконтактных областей NReserve D 24 −3 12 −3 =
- 19. Заключение В ходе работы были: ) Исследована модель токопереноса через гетеростуктуру с учетом самосогласованного потенциала; )
- 21. Скачать презентацию








 Выполнила: ученица 10класса МОУ СОШ №14 Чекундинского сельского поселения. Журавлева Лариса.
Выполнила: ученица 10класса МОУ СОШ №14 Чекундинского сельского поселения. Журавлева Лариса. Интернет сайты: знакомимся, изучаем, учимся на примерах педагогов России
Интернет сайты: знакомимся, изучаем, учимся на примерах педагогов России Компьютерные игры. Рисование огнём
Компьютерные игры. Рисование огнём Разработка (оформление) презентации под ключ
Разработка (оформление) презентации под ключ Тенденции web-дизайна
Тенденции web-дизайна Диаграмма и её виды
Диаграмма и её виды Синтез цифровой системы автоматического регулирования угловой скорости электродвигателя
Синтез цифровой системы автоматического регулирования угловой скорости электродвигателя Средства обеспечения безопасности информации
Средства обеспечения безопасности информации Трояны
Трояны Убираем белый фон. Инструмент Волшебная палочка
Убираем белый фон. Инструмент Волшебная палочка Практическая работа №4. Настройка VPN
Практическая работа №4. Настройка VPN Госслужащие и социальные сети
Госслужащие и социальные сети 7-1-5
7-1-5 Textovye_redaktory
Textovye_redaktory Виды и форматы электронных изданий
Виды и форматы электронных изданий Интернет: интересно, полезно, безопасно!
Интернет: интересно, полезно, безопасно! Основы рисования в Microsoft Word
Основы рисования в Microsoft Word Implementation of std::common_type
Implementation of std::common_type Достучаться до поколения Z
Достучаться до поколения Z База данных (БД)
База данных (БД) Онлайн магазин Avon
Онлайн магазин Avon Роль средств массовой информации
Роль средств массовой информации Носители информации
Носители информации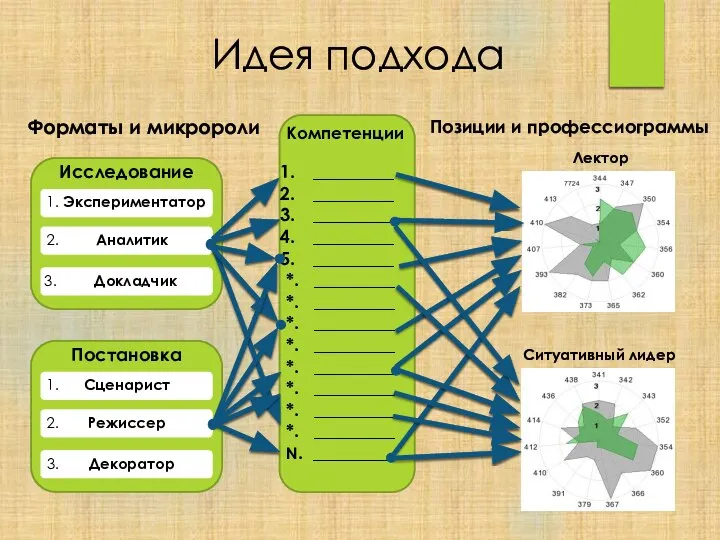 Идея подхода. Форматы и микророли. Исследование
Идея подхода. Форматы и микророли. Исследование Портал Дошкола Тилли
Портал Дошкола Тилли Обзор активности конкурентов в интернете
Обзор активности конкурентов в интернете Основы алгоритмизации
Основы алгоритмизации Системное моделирование
Системное моделирование