- Главная
- Информатика
- Сложение двоичных чисел в коде прямого замещения (Д1)

Содержание
- 2. Сложение двоичных чисел в коде прямого замещения (Д1) 184+298=482 0001 1000 0100 0010 1001 1000 --------------------------------
- 3. Вычитание двоичных чисел в коде прямого замещения (Д1) 0110 0001 0101 0011 1001 0110 -----------------------------0010→0111→1111 0000
- 4. Знаковый разряд двоичных чисел весом 2m для целых и 20 для дробных чисел участвует совместно с
- 5. Сложение в коде D1 с использованием обратного кода Рассмотрим сложение чисел: -298+127=-171 Предварительно перед сложением представим
- 7. Скачать презентацию
Слайд 2Сложение двоичных чисел в коде прямого замещения (Д1)
184+298=482
0001 1000 0100
0010 1001 1000
--------------------------------
1100
0001
0100
>10
перенос
<10
1100
0001
0100
0000 0110 0110
-------------------------------
+
0100 1000 0010
4
8
2
На
Сложение двоичных чисел в коде прямого замещения (Д1)
184+298=482
0001 1000 0100
0010 1001 1000
--------------------------------
1100
0001
0100
>10
перенос
<10
1100
0001
0100
0000 0110 0110
-------------------------------
+
0100 1000 0010
4
8
2
На

Слайд 3Вычитание двоичных чисел в коде прямого замещения (Д1)
0110 0001 0101
0011 1001 0110
-----------------------------0010→0111→1111
0000 0110 0110
------------------------------
0010 0001
Вычитание двоичных чисел в коде прямого замещения (Д1)
0110 0001 0101
0011 1001 0110
-----------------------------0010→0111→1111
0000 0110 0110
------------------------------
0010 0001
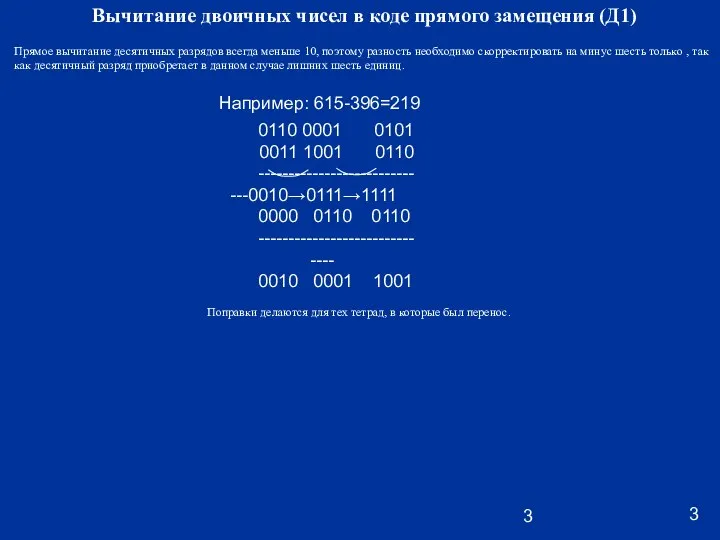
Например: 615-396=219
Прямое вычитание десятичных разрядов всегда меньше 10, поэтому разность необходимо скорректировать на минус шесть только , так как десятичный разряд приобретает в данном случае лишних шесть единиц.
Поправки делаются для тех тетрад, в которые был перенос.
Слайд 4Знаковый разряд двоичных чисел весом 2m для целых и 20 для дробных
Знаковый разряд двоичных чисел весом 2m для целых и 20 для дробных
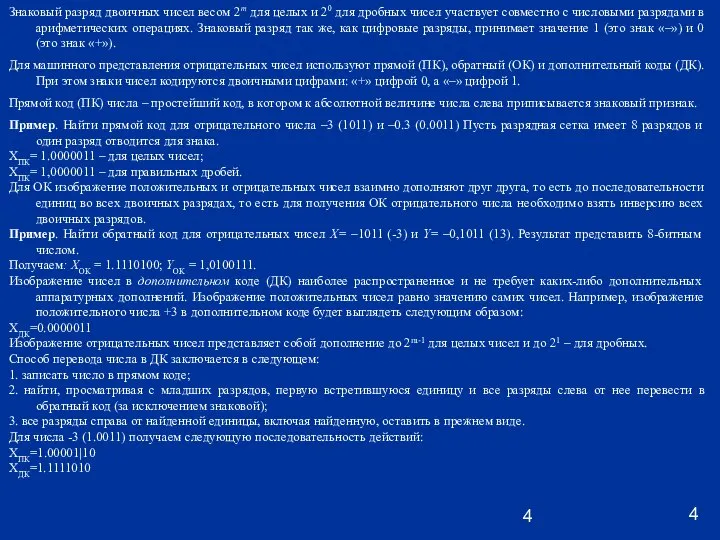
Для машинного представления отрицательных чисел используют прямой (ПК), обратный (ОК) и дополнительный коды (ДК). При этом знаки чисел кодируются двоичными цифрами: «+» цифрой 0, а «–» цифрой 1.
Прямой код (ПК) числа – простейший код, в котором к абсолютной величине числа слева приписывается знаковый признак.
Пример. Найти прямой код для отрицательного числа –3 (1011) и –0.3 (0.0011) Пусть разрядная сетка имеет 8 разрядов и один разряд отводится для знака.
ХПК= 1.0000011 – для целых чисел;
ХПК= 1,0000011 – для правильных дробей.
Для ОК изображение положительных и отрицательных чисел взаимно дополняют друг друга, то есть до последовательности единиц во всех двоичных разрядах, то есть для получения ОК отрицательного числа необходимо взять инверсию всех двоичных разрядов.
Пример. Найти обратный код для отрицательных чисел X= –1011 (-3) и Y= –0,1011 (13). Результат представить 8-битным числом.
Получаем: XОК = 1.1110100; YОК = 1,0100111.
Изображение чисел в дополнительном коде (ДК) наиболее распространенное и не требует каких-либо дополнительных аппаратурных дополнений. Изображение положительных чисел равно значению самих чисел. Например, изображение положительного числа +3 в дополнительном коде будет выглядеть следующим образом:
ХДК=0.0000011
Изображение отрицательных чисел представляет собой дополнение до 2m-1 для целых чисел и до 21 – для дробных.
Способ перевода числа в ДК заключается в следующем:
1. записать число в прямом коде;
2. найти, просматривая с младших разрядов, первую встретившуюся единицу и все разряды слева от нее перевести в обратный код (за исключением знаковой);
3. все разряды справа от найденной единицы, включая найденную, оставить в прежнем виде.
Для числа -3 (1.0011) получаем следующую последовательность действий:
ХПК=1.00001|10
ХДК=1.1111010
Слайд 5Сложение в коде D1 с использованием обратного кода
Рассмотрим сложение чисел:
-298+127=-171
Предварительно перед
Сложение в коде D1 с использованием обратного кода
Рассмотрим сложение чисел:
-298+127=-171
Предварительно перед

-298ПК: 1. 0010 1001 1000
-298ОК: 1. 0111 0000 0001
В данном случае для дополнения младшей тетрады до числа 9 необходимо число 1, для дополнения второй тетрады необходим ноль, а для дополнения старшей тетрады – число 7. После перевода отрицательного числа в ОК проводим основной цикл сложения:
1. 0111 0000 0001
0. 0001 0010 0111
------------------------
1. 1000 0010 1000
Получили результат, записанный в обратном коде. Для получения конечного результата находим его дополнение до числа 9. Аналогично, дополняя разряды до девяти, получаем:
1. 0001 0111 0001 или -171.
При этом необходимо учитывать, что если существует перенос из знакового разряда, то эту единицу прибавляем к младшей тетраде.
 Кодирование информации
Кодирование информации Механизм обработки и генерирования исключительных ситуаций. Лекция 21
Механизм обработки и генерирования исключительных ситуаций. Лекция 21 Rukki. Проект для строителей
Rukki. Проект для строителей Алгоритмизация и программирование С#. (Лекция 1.1)
Алгоритмизация и программирование С#. (Лекция 1.1) Осциллограф портативный FNIRSI DSO 2031H
Осциллограф портативный FNIRSI DSO 2031H Разница между проводным и беспроводным подключением
Разница между проводным и беспроводным подключением Единый региональный информационный просветительский проект
Единый региональный информационный просветительский проект Управление микроклиматом фермерской теплицы
Управление микроклиматом фермерской теплицы Требования к интернет-системам
Требования к интернет-системам Kodlayici (encoder)
Kodlayici (encoder) Telegram-бот Медицинский консультант
Telegram-бот Медицинский консультант Нелинейная детерминированная система
Нелинейная детерминированная система Интерфейс графических редакторов
Интерфейс графических редакторов Викторина по информатике
Викторина по информатике SpegilMynd Present. Правила игры
SpegilMynd Present. Правила игры Что такое Osint?
Что такое Osint? Сайт
Сайт Работа с формулами в MS Excel
Работа с формулами в MS Excel Графический интерфейс операционной системы
Графический интерфейс операционной системы Разработка игры “Sokoban”
Разработка игры “Sokoban” Сервис Bot Money
Сервис Bot Money Словесные информационные модели
Словесные информационные модели Этапы проектирования ИС с применением UML
Этапы проектирования ИС с применением UML Кодирование и декодирование данных
Кодирование и декодирование данных Мультимедиа. Классификация
Мультимедиа. Классификация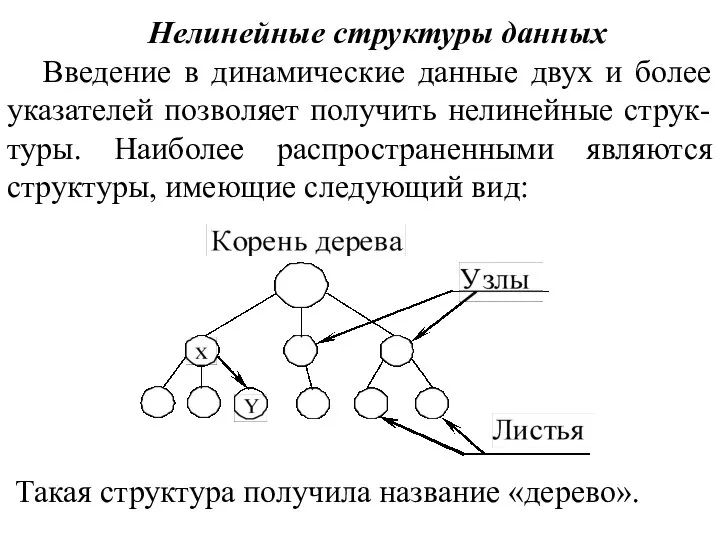 Нелинейные структуры данных. Тема 5
Нелинейные структуры данных. Тема 5 Электронная подпись для ЕГАИС
Электронная подпись для ЕГАИС Что такое Page Object
Что такое Page Object