Содержание
- 2. Цели и задачи Цель: Моделирование четырёхмерных пространств с использованием современных технологий. Задачи: Изучить модели одномерного, двумерного
- 3. Пространство Чёткого определения у пространства нет, но существуют рассуждения по описанию и определению этого понятия. Наиболее
- 4. Создание пространств из точки. Для начала возьмём нульмерное пространство – точку, и скопируем её на некоторую
- 5. Создание пространств из точки. Аналогично мы делаем и с квадратом, создавая из него куб, и, наконец,
- 6. Многомерные фигуры Благодаря ортогональным проекциям мы можем увидеть форму тел, спроецировав их на измерение n-1. Здесь
- 7. Вот пример ортогональное проекции гиперкуба. Мы видим стержни двух кубов, соединённых вершинами. Многомерные фигуры
- 8. Гиперсфера и пятиячейник Одни из четырёхмерных фигур это четырёхмерная сфера - гиперсфера и пятиячейник.
- 9. Для примера возьмем плоскость двигающуюся сквозь трёхмерное пространство. Как мы видим срез сферы, при движении плоскости
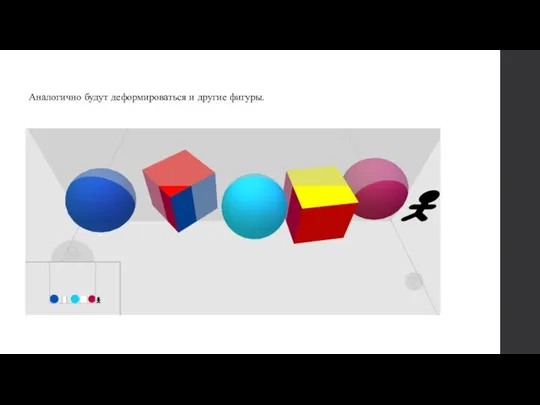
- 10. Аналогично будут деформироваться и другие фигуры.
- 11. Аналогично будет моделироваться и четырёхмерное пространство. Мы будем видеть срез четырёхмерной фигуры. Вот один из примеров.
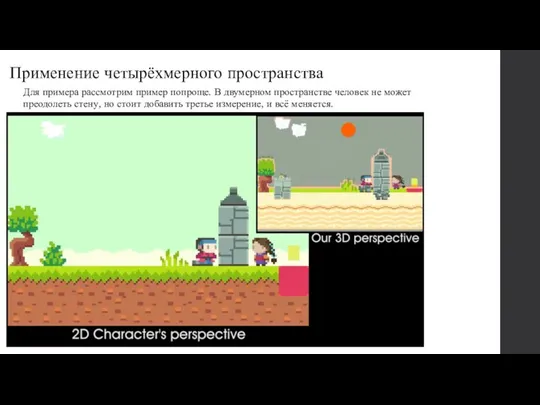
- 12. Применение четырёхмерного пространства Для примера рассмотрим пример попроще. В двумерном пространстве человек не может преодолеть стену,
- 13. Теперь та же самая ситуация, но с третьим и четвёртым измерениями. Применение четырёхмерного пространства
- 14. В то время как на компьютерах мы можем моделировать многомерные пространства, то развёртки четырёхмерных фигур мы
- 16. Скачать презентацию











 Альбом. Дипломное проектирование
Альбом. Дипломное проектирование Разработка функционала информационной системы для автоматизации деятельности индивидуального предпринимателя
Разработка функционала информационной системы для автоматизации деятельности индивидуального предпринимателя Образец Защита проекта
Образец Защита проекта Разработка электронного учебника по дисциплине Сети ЭВМ и телекоммуникаций
Разработка электронного учебника по дисциплине Сети ЭВМ и телекоммуникаций Тестовое задание для Frontend разработчика
Тестовое задание для Frontend разработчика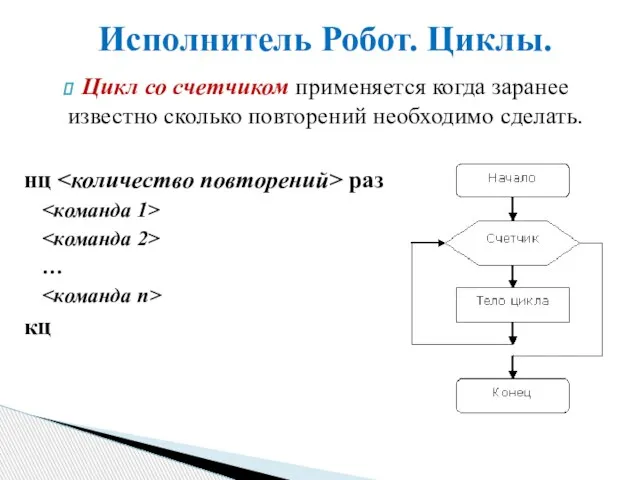 Исполнитель Робот. Циклы
Исполнитель Робот. Циклы Анализ проблемы и моделирование предметной области с использованием системного подхода
Анализ проблемы и моделирование предметной области с использованием системного подхода Децентрализованная самостоятельная видеоплощадка с поддержкой NFT
Децентрализованная самостоятельная видеоплощадка с поддержкой NFT Функции И+ПРГ C \ С++
Функции И+ПРГ C \ С++ Neom. Crowd Funder: Motion Principles
Neom. Crowd Funder: Motion Principles Средства мультимедиа
Средства мультимедиа Информационные процессы. Информация в жизни человека. Понятие информационных ресурсов. Роль информационных ресурсов в развитии
Информационные процессы. Информация в жизни человека. Понятие информационных ресурсов. Роль информационных ресурсов в развитии Безопасность в сети Интернет
Безопасность в сети Интернет Файловый архивы
Файловый архивы Основные режимы работы табличного редактора
Основные режимы работы табличного редактора Разработка мобильного приложения для контроля соблюдения ПДД
Разработка мобильного приложения для контроля соблюдения ПДД Гибридные информационные системы в промышленности
Гибридные информационные системы в промышленности Использование диаграмм Эйлера-Венна при решении логических задач
Использование диаграмм Эйлера-Венна при решении логических задач Понятие операционного окружения, состав, назначение
Понятие операционного окружения, состав, назначение Lektsia_1_Word
Lektsia_1_Word Анализ средств и методов администрирования сети
Анализ средств и методов администрирования сети Обзор решений (продуктов) для обеспечения безопасности баз данных
Обзор решений (продуктов) для обеспечения безопасности баз данных Фотография и компьютер. Документ или фальсификация: факт и его компьютерная трактовка
Фотография и компьютер. Документ или фальсификация: факт и его компьютерная трактовка Планета алгоритмика. Клад
Планета алгоритмика. Клад Сетевая модель OSI
Сетевая модель OSI Алгоритмическая конструкция ветвление. Основные алгоритмические конструкции
Алгоритмическая конструкция ветвление. Основные алгоритмические конструкции Алгоритмический турнир
Алгоритмический турнир 5. Python-3 Управляющие конструкции
5. Python-3 Управляющие конструкции