Статистические методы в искусственном интеллекте. Предсказание. Наивный Байесовский алгоритм и реализация Байесовского выражения

Представьте себе следующую ситуацию: вы работаете над задачей классификации, уже создали набор гипотез и сформировали признаки. Через час заказчики хотят увидеть первый вариант модели.
Перед вами обучающий набор данных, содержащий несколько сотен тысяч элементов и большое количество признаков. Что вы будете делать? На вашем месте я бы воспользовался наивным байесовским алгоритмом (naive Bayes algorithm, НБА), который превосходит по скорости многие другие алгоритмы классификации. В его основе лежит теорема Байеса.

Содержание
Что такое наивный байесовский алгоритм?
Как он работает?
Положительные и отрицательные.
4 приложения наивного байесовского алгоритма.
Как создать базовую модель на его основе с помощью Python?
Советы по оптимизации модели.

Что такое наивный байесовский алгоритм?
Наивный байесовский алгоритм – это алгоритм классификации, основанный на теореме Байеса с допущением о независимости признаков. Другими словами, НБА предполагает, что наличие какого-либо признака в классе не связано с наличием какого-либо другого признака. Например, фрукт может считаться яблоком, если он красный, круглый и его диаметр составляет порядка 8 сантиметров. Даже если эти признаки зависят друг от друга или от других признаков, в любом случае они вносят независимый вклад в вероятность того, что этот фрукт является яблоком. В связи с таким допущением алгоритм называется «наивным».
Модели на основе НБА достаточно просты и крайне полезны при работе с очень большими наборами данных. При своей простоте НБА способен превзойти даже некоторые сложные алгоритмы классификации.

Теорема Байеса позволяет рассчитать апостериорную вероятность P(c|x) на основе P(c), P(x) и P(x|c).
P(c|x) – апостериорная вероятность данного класса c (т.е. данного значения целевой переменной) при данном значении признака x.
P(c) – априорная вероятность данного класса.
P(x|c) – правдоподобие, т.е. вероятность данного значения признака при данном классе.
P(x) – априорная вероятность данного значения признака.

Как работает наивный байесовский алгоритм?
Давайте рассмотрим пример. Ниже представлен обучающий набор данных, содержащий один признак «Погодные условия» (weather) и целевую переменную «Игра» (play), которая обозначает возможность проведения матча. На основе погодных условий мы должны определить, состоится ли матч. Чтобы сделать это, необходимо выполнить следующие шаги.
Шаг 1. Преобразуем набор данных в частотную таблицу (frequency table).
Шаг 2. Создадим таблицу правдоподобия (likelihood table), рассчитав соответствующие вероятности. Например, вероятность облачной погоды (overcast) составляет 0,29, а вероятность того, что матч состоится (yes) – 0,64.

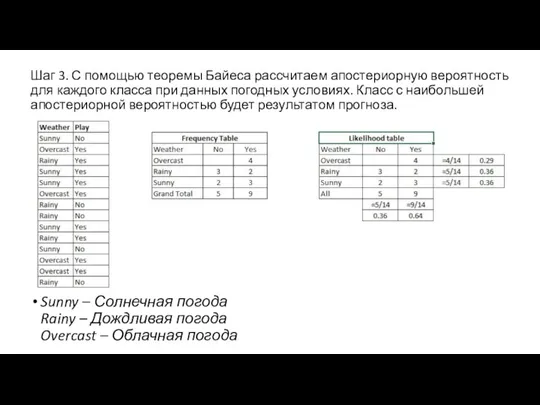
Шаг 3. С помощью теоремы Байеса рассчитаем апостериорную вероятность для каждого класса при данных погодных условиях. Класс с наибольшей апостериорной вероятностью будет результатом прогноза.
Sunny – Солнечная погода
Rainy – Дождливая погода
Overcast – Облачная погода

Задача. Состоится ли матч при солнечной погоде (sunny)?
Мы можем решить эту задачу с помощью описанного выше подхода.
P(Yes | Sunny) = P(Sunny | Yes) * P(Yes) / P(Sunny)
Здесь мы имеем следующие значения:
P(Sunny | Yes) = 3 / 9 = 0,33
P(Sunny) = 5 / 14 = 0,36
P(Yes) = 9 / 14 = 0,64
Теперь рассчитаем P(Yes | Sunny):
P(Yes | Sunny) = 0,33 * 0,64 / 0,36 = 0,60
Значит, при солнечной погоде более вероятно, что матч состоится.
Аналогичным образом с помощью НБА можно прогнозировать несколько различных классов на основе множества признаков. Этот алгоритм в основном используется в области классификации текстов и при решении задач многоклассовой классификации.

Положительные и отрицательные стороны наивного байесовского алгоритма
Положительные стороны:
Классификация, в том числе многоклассовая, выполняется легко и быстро.
Когда допущение о независимости выполняется, НБА превосходит другие алгоритмы, такие как логистическая регрессия (logistic regression), и при этом требует меньший объем обучающих данных.
НБА лучше работает с категорийными признаками, чем с непрерывными. Для непрерывных признаков предполагается нормальное распределение, что является достаточно сильным допущением.

Отрицательные стороны:
Если в тестовом наборе данных присутствует некоторое значение категорийного признака, которое не встречалось в обучающем наборе данных, тогда модель присвоит нулевую вероятность этому значению и не сможет сделать прогноз. Это явление известно под названием «нулевая частота» (zero frequency). Данную проблему можно решить с помощью сглаживания. Одним из самых простых методов является сглаживание по Лапласу (Laplace smoothing).
Хотя НБА является хорошим классификатором, значения спрогнозированных вероятностей не всегда являются достаточно точными. Поэтому не следует слишком полагаться на результаты, возвращенные методом predict_proba.
Еще одним ограничением НБА является допущение о независимости признаков. В реальности наборы полностью независимых признаков встречаются крайне редко.

4 приложения наивного байесовского алгоритма
Классификация в режиме реального времени. НБА очень быстро обучается, поэтому его можно использовать для обработки данных в режиме реального времени.
Многоклассовая классификация. НБА обеспечивает возможность многоклассовой классификации. Это позволяет прогнозировать вероятности для множества значений целевой переменной.
Классификация текстов, фильтрация спама, анализ тональности текста. При решении задач, связанных с классификацией текстов, НБА превосходит многие другие алгоритмы. Благодаря этому, данный алгоритм находит широкое применение в области фильтрации спама (идентификация спама в электронных письмах) и анализа тональности текста (анализ социальных медиа, идентификация позитивных и негативных мнений клиентов).
Рекомендательные системы. Наивный байесовский классификатор в сочетании с коллаборативной фильтрацией (collaborative filtering) позволяет реализовать рекомендательную систему. В рамках такой системы с помощью методов машинного обучения и интеллектуального анализа данных новая для пользователя информация отфильтровывается на основании спрогнозированного мнения этого пользователя о ней.

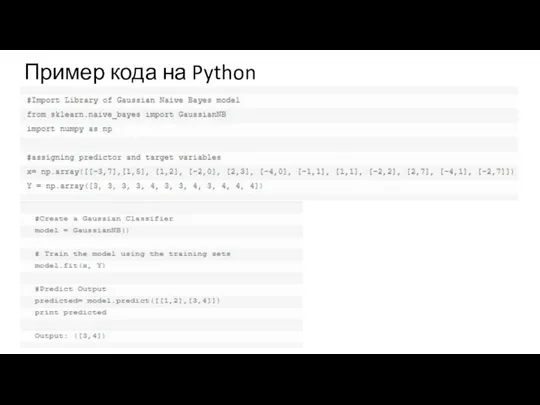
Как создать базовую модель на основе наивного байесовского алгоритма с помощью Python?
В этом нам поможет библиотека scikit-learn. Данная библиотека содержит три типа моделей на основе наивного байесовского алгоритма:
Gaussian (нормальное распределение). Модель данного типа используется в случае непрерывных признаков и предполагает, что значения признаков имеют нормальное распределение.
Multinomial (мультиномиальное распределение). Используется в случае дискретных признаков. Например, в задаче классификации текстов признаки могут показывать, сколько раз каждое слово встречается в данном тексте.
Bernoulli (распределение Бернулли). Используется в случае двоичных дискретных признаков (могут принимать только два значения: 0 и 1). Например, в задаче классификации текстов с применением подхода «мешок слов» (bag of words) бинарный признак определяет присутствие (1) или отсутствие (0) данного слова в тексте.
В зависимости от набора данных вы можете выбрать подходящую модель из описанных выше. Далее представлен пример кода для модели Gaussian.

Пример кода на Python

Пример:
Байесовский классификатор относится к разряду машинного обучения. Суть такова: система, перед которой стоит задача определить, является ли следующее письмо спамом, заранее обучена каким-то количеством писем точно известных где «спам», а где «не спам». Уже стало понятно, что это обучение с учителем, где в роли учителя выступаем мы. Байесовский классификатор представляет документ (в нашем случае письмо) в виде набора слов, которые якобы не зависят друг от друга (вот от сюда и вытекает та самая наивность).

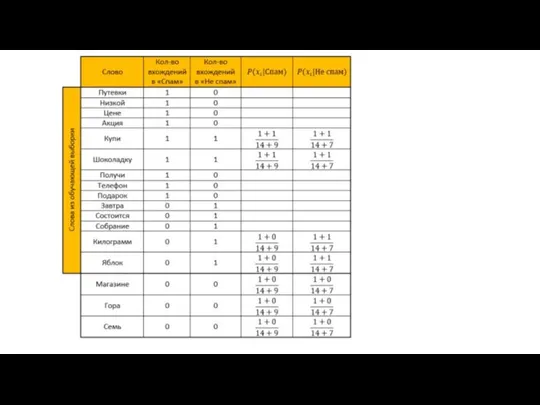
Необходимо рассчитать оценку для каждого класса (спам/не спам) и выбрать ту, которая получилась максимальной. Для этого используем следующую формулу:

Когда объем текста очень большой, приходится работать с очень маленькими числами. Для того чтобы этого избежать, можно преобразовать формулу по свойству логарифма**:
Подставляем и получаем:

*Во время выполнения подсчетов вам может встретиться слово, которого не было на этапе обучения системы. Это может привести к тому, что оценка будет равна нулю и документ нельзя будет отнести ни в одну из категорий (спам/не спам). Как бы вы не хотели, вы не обучите свою систему всем возможным словам. Для этого необходимо применить сглаживание, а точнее – сделать небольшие поправки во все вероятности вхождения слов в документ. Выбирается параметр 0<α≤1 (если α=1, то это сглаживание Лапласа)
**Логарифм – монотонно возрастающая функция. Как видно из первой формулы – мы ищем максимум. Логарифм от функции достигнет максимума в той же точке (по оси абсцисс), что и сама функция. Это упрощает вычисление, ибо меняется только численное значение.

От теории к практике
Пусть наша система обучалась на следующих письмам, заранее известных где «спам», а где «не спам» (обучающая выборка):
Спам:
«Путевки по низкой цене»
«Акция! Купи шоколадку и получи телефон в подарок»
Не спам:
«Завтра состоится собрание»
«Купи килограмм яблок и шоколадку»

Задание: определить, к какой категории отнести следующее письмо:
«В магазине гора яблок. Купи семь килограмм и шоколадку»
Решение:
Составляем таблицу. Убираем все «стоп-слова», рассчитываем вероятности, параметр для сглаживания принимаем за единицу.

Оценка для категории «Спам»:
Оценка для категории «Не спам»:
Ответ: оценка «Не спам» больше оценки «Спам». Значит проверочное письмо — не спам!

То же самое рассчитаем и с помощью функции, преобразованной по свойству логарифма:
Оценка для категории «Спам»:
Оценка для категории «Не спам»:
Ответ: аналогично предыдущему ответу. Проверочное письмо – не спам!

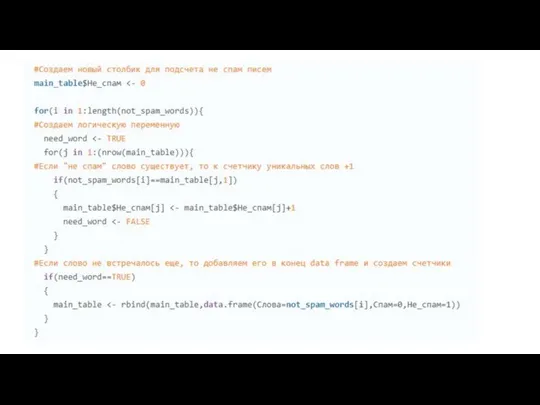
Реализация на языке программирования R

#Используем ту же логическую переменную, чтобы не создавать новую
need_word <- TRUE
for(j in 1:nrow(main_table))
{
#Если слово из проверочного письма уже существует в нашей выборке то считаем вероятность каждой категории
if(test_letter[i]==main_table$Слова[j])
{
main_table$Вероятность_спам[j] <- formula_1(main_table$Спам[j],quantity,sum(main_table$Спам)) main_table$Вероятность_не_спам[j] <- formula_1(main_table$Не_спам[j],quantity,sum(main_table$Не_спам))
need_word <- FALSE } }
#Если слова нет, то добавляем его в конец data frame, и считаем вероятность спама/не спама if(need_word==TRUE)
{
main_table <- rbind(main_table,data.frame(Слова=test_letter[i],Спам=0,Не_спам=0,Вероятность_спам=NA,Вероятность_не_спам=NA))
main_table$Вероятность_спам[nrow(main_table)] <- formula_1(main_table$Спам[nrow(main_table)],quantity,sum(main_table$Спам)) main_table$Вероятность_не_спам[nrow(main_table)] <- formula_1(main_table$Не_спам[nrow(main_table)],quantity,sum(main_table$Не_спам)) } }