Свойства логических операций

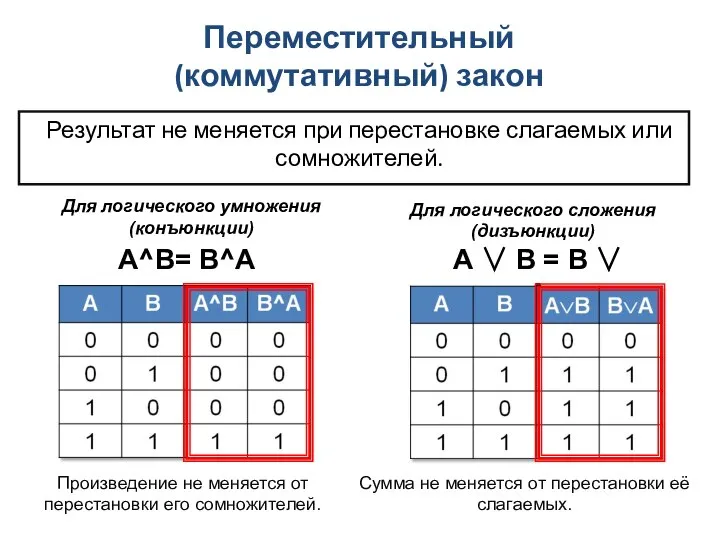
Переместительный
(коммутативный) закон
Результат не меняется при перестановке слагаемых или сомножителей.
Для логического умножения (конъюнкции)
A^B= B^A
Для логического сложения (дизъюнкции)
A ∨ B = B ∨ A
Сумма не меняется от перестановки её слагаемых.
Произведение не меняется от перестановки его сомножителей.

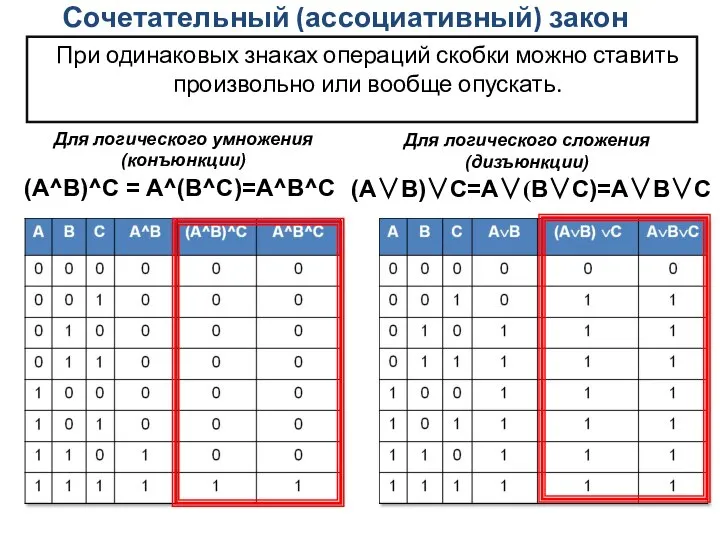
Сочетательный (ассоциативный) закон
При одинаковых знаках операций скобки можно ставить произвольно или вообще опускать.
Для логического умножения (конъюнкции)
(A^B)^C = A^(B^C)=A^B^C
Для логического сложения (дизъюнкции)
(A∨B)∨C=A∨(B∨C)=A∨B∨C

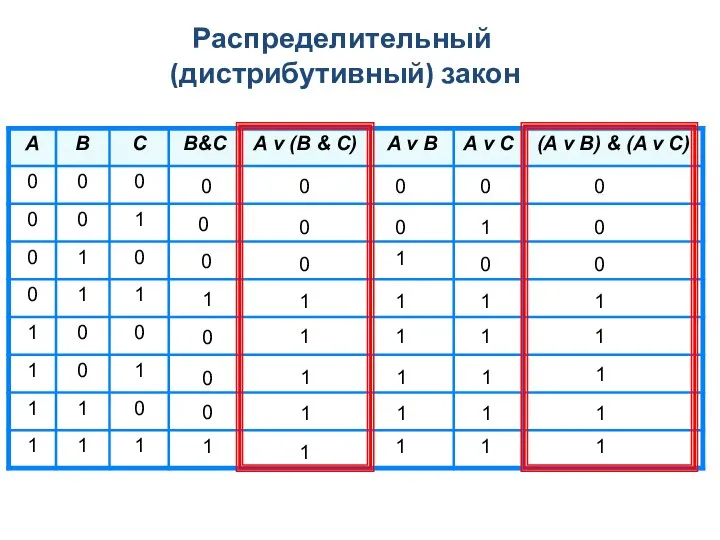
Распределительный
(дистрибутивный) закон
Операцию можно выполнить по частям – для каждого слагаемого, входящего во второй сомножитель.
Для логического умножения (конъюнкции)
A ^ (B ∨ C)
=
(A ^ B) ∨ (A ^ C)
Для логического сложения (дизъюнкции)
A ∨ (B ^ C)
=
(A ∨ B) ^ (A ∨ C)

Распределительный
(дистрибутивный) закон
0
0
0
0
0
0
1
1
0
0
0
1
1
1
1
1
0
0
1
1
1
1
1
1
0
0
1
1
1
1
1
1
0
0
0
1
1
1
1
1

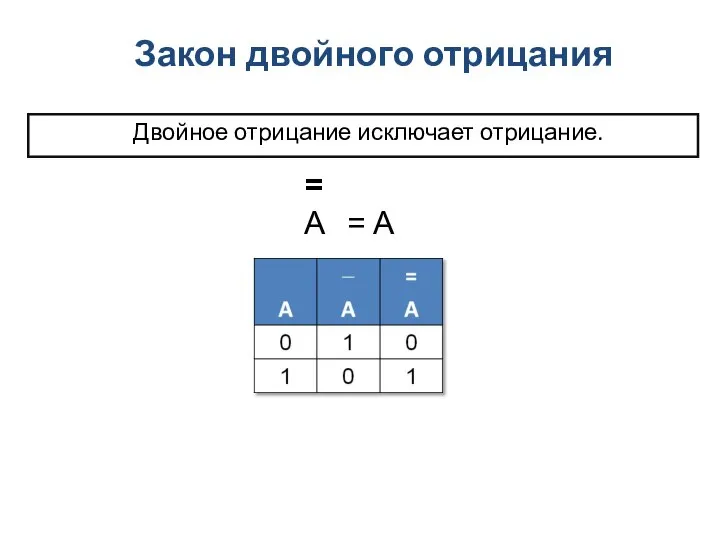
Закон двойного отрицания
Двойное отрицание исключает отрицание.
=
A
= A

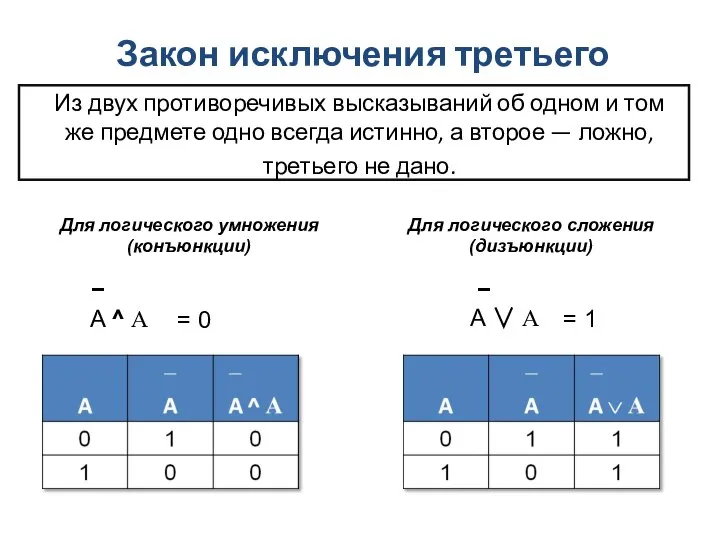
Закон исключения третьего
Из двух противоречивых высказываний об одном и том же предмете одно всегда истинно, а второе — ложно,
третьего не дано.
Для логического умножения (конъюнкции)
Для логического сложения (дизъюнкции)
−
A ^ A
= 0
−
A ∨ A
= 1

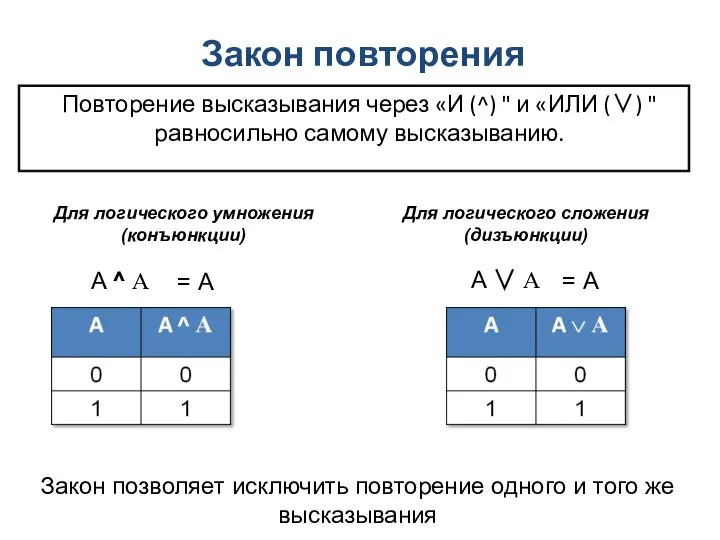
Закон повторения
Повторение высказывания через «И (^) " и «ИЛИ (∨) " равносильно самому высказыванию.
Для логического умножения (конъюнкции)
Для логического сложения (дизъюнкции)
A ^ A
= А
A ∨ A
= А
Закон позволяет исключить повторение одного и того же высказывания

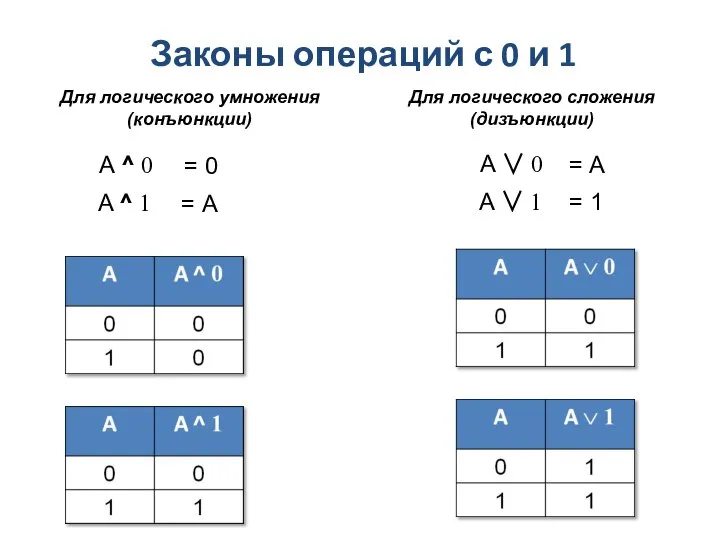
Законы операций с 0 и 1
Для логического умножения (конъюнкции)
Для логического сложения (дизъюнкции)
A ^ 0
= 0
A ∨ 0
= А
A ^ 1
= А
A ∨ 1
= 1

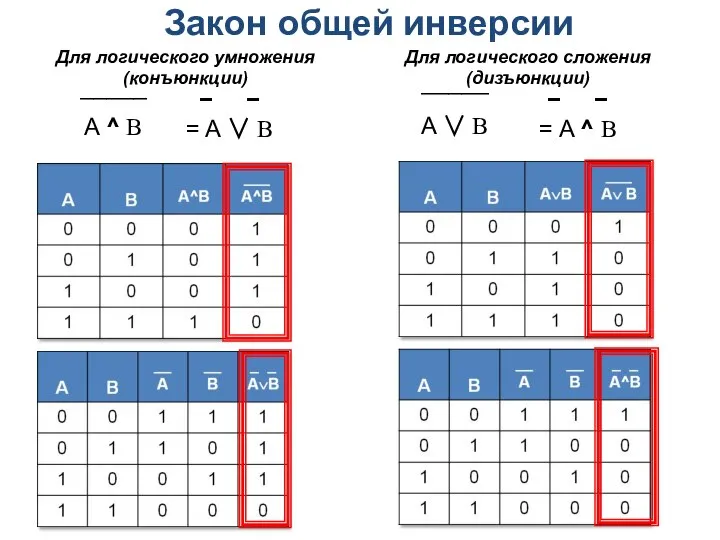
Закон общей инверсии
Для логического умножения (конъюнкции)
Для логического сложения (дизъюнкции)
A ^ B − −
= A ∨ B
_____
A ∨ B
− −
= A ^ B
_____

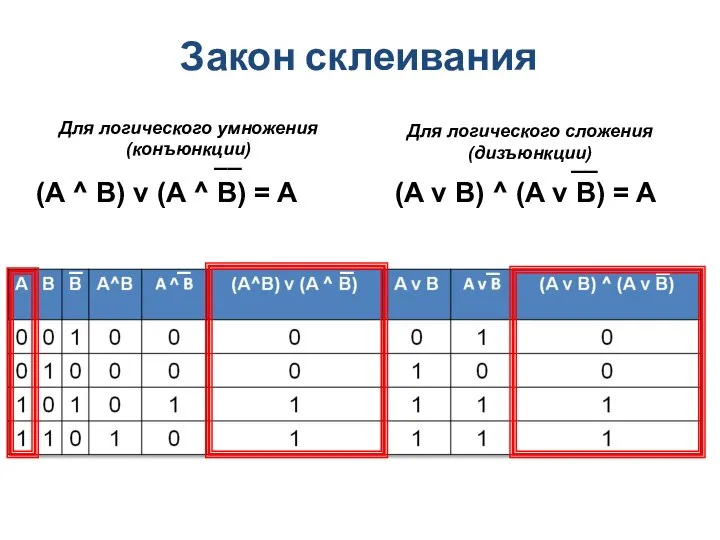
Закон склеивания
Для логического умножения (конъюнкции)
(A ^ B) v (A ^ B) = A
Для логического сложения (дизъюнкции)
__
(A v B) ^ (A v B) = A
__
_
_
_
_
_