Содержание
- 2. Для чего нужно сжатие данных? Уменьшение V памяти для хранения ЭКГ в автоматизированных архивах Снижение требований
- 3. Структурные методы сжатия Осуществляется контроль абсолютной ошибки при определении избыточных отсчетов и выборе существенных ординат Суть
- 4. Двухпараметрическая адаптация (повышает эффективность апертурных методов сжатия, автоматически определяет длительность интервала аппроксимизации и степень аппроксимизирующего полинома)
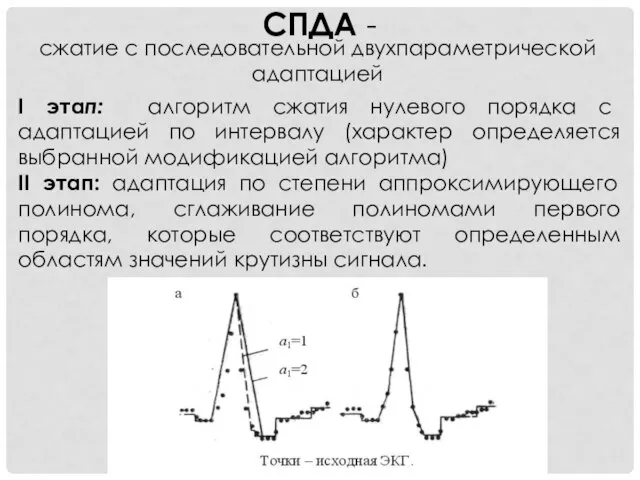
- 5. СПДА - сжатие с последовательной двухпараметрической адаптацией I этап: алгоритм сжатия нулевого порядка с адаптацией по
- 6. На первом этапе используется интерполяционный алгоритм сжатия нулевого порядка для сокращенного представления сигнала. При поступлении каждого
- 7. На втором этапе построения сжатого сигнала каждый j-й участок анализируется на возможность сглаживания полиномами первого порядка.
- 8. Выходными параметрами сжатого сигнала на k-ом участке аппроксимации будут величины Vk и τk определяемые выражениями а
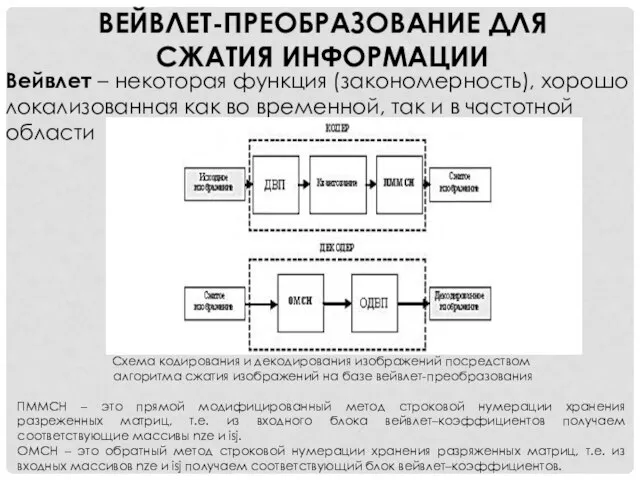
- 9. ВЕЙВЛЕТ-ПРЕОБРАЗОВАНИЕ ДЛЯ СЖАТИЯ ИНФОРМАЦИИ Вейвлет – некоторая функция (закономерность), хорошо локализованная как во временной, так и
- 10. Для оценки результатов алгоритма не только по эффективности сжатия, но и по степени достоверности восстановленного изображения
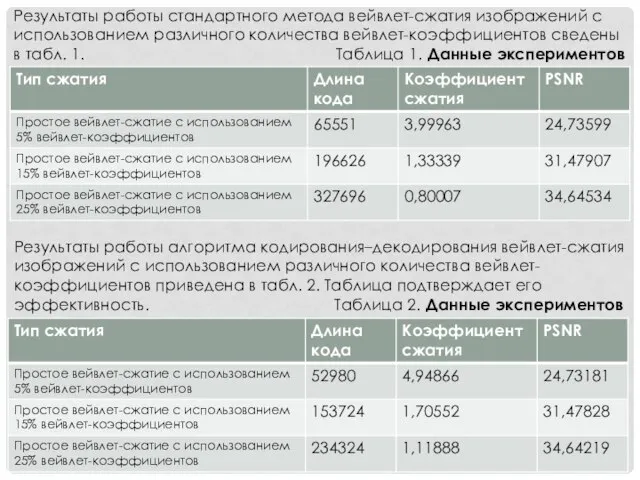
- 11. Результаты работы стандартного метода вейвлет-сжатия изображений с использованием различного количества вейвлет-коэффициентов cведены в табл. 1. Таблица
- 12. Исходное изображение «goldhill.pgm» размерностью 512х512, длина кода изображения 262180 байтов. Исходное изображение «goldhill.pgm» к которому был
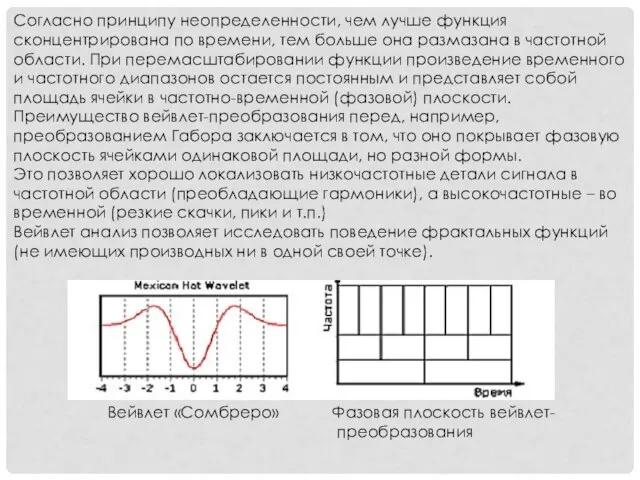
- 13. Согласно принципу неопределенности, чем лучше функция сконцентрирована по времени, тем больше она размазана в частотной области.
- 14. Разрешающая способность анализа во временной области возрастает с ростом частоты, что является принципиальным отличием анализа в
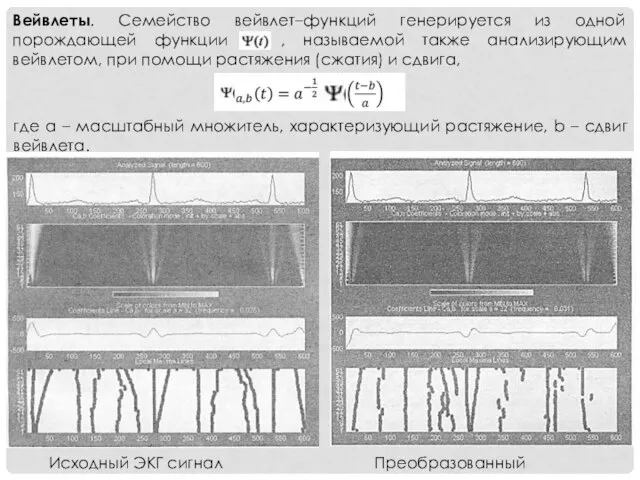
- 15. Исходный ЭКГ сигнал Преобразованный Вейвлеты. Семейство вейвлет–функций генерируется из одной порождающей функции , называемой также анализирующим
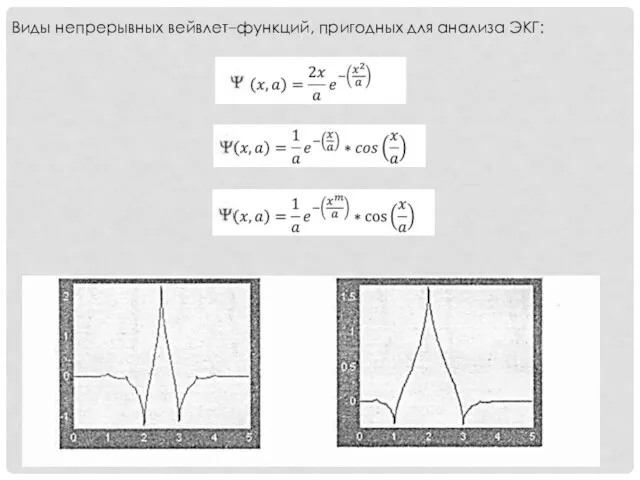
- 16. Виды непрерывных вейвлет–функций, пригодных для анализа ЭКГ:
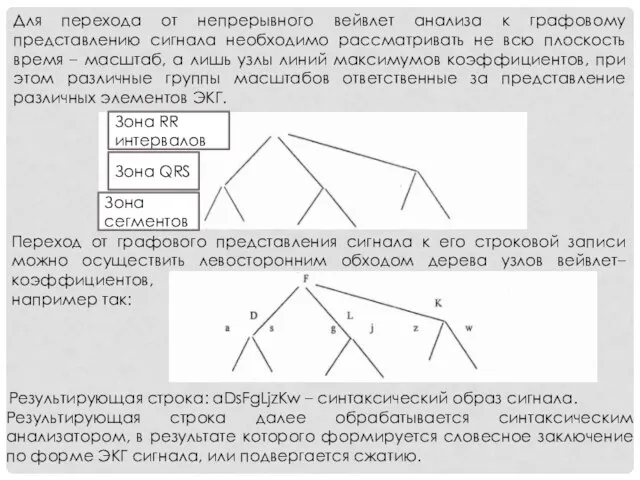
- 17. Результирующая строка далее обрабатывается синтаксическим анализатором, в результате которого формируется словесное заключение по форме ЭКГ сигнала,
- 18. Алгоритм JPEG2000 Основные отличия алгоритма в JPEG 2000 от алгоритма JPEG заключаются в следующем: Лучшее качество
- 19. Шаг 1. В JPEG-2000 предусмотрен сдвиг яркости (DC level shift) каждой компоненты (RGB) изображения перед преобразованием
- 20. Шаг 3. Дискретное wavelet-преобразование (DWT) также может быть двух видов – для случая сжатия с потерями
- 22. Скачать презентацию











 L_6_2
L_6_2 Дискретное (цифровое) представление различной информации
Дискретное (цифровое) представление различной информации Все события в одном мобильном приложении
Все события в одном мобильном приложении ДП
ДП Открытая дискуссия в рамках проекта Путь к цифре. 7 класс
Открытая дискуссия в рамках проекта Путь к цифре. 7 класс Адресация в Интернете
Адресация в Интернете Ввод информации в память компьютера. 5 класс
Ввод информации в память компьютера. 5 класс Количество информации по Шеннону
Количество информации по Шеннону Исполнитель Робот
Исполнитель Робот Регистрации на портале госуслуги
Регистрации на портале госуслуги Программный комплекс AutoCad
Программный комплекс AutoCad Франчайзинг. Проведение фотомониторинга
Франчайзинг. Проведение фотомониторинга Цифровизация в сфере государственного регулирования тарифов на тепловую энергию
Цифровизация в сфере государственного регулирования тарифов на тепловую энергию Оформление проектов
Оформление проектов 85 из 70. Темы 6-11
85 из 70. Темы 6-11 Innovative technologies of event-management in the field of media and information literacy (MIL)
Innovative technologies of event-management in the field of media and information literacy (MIL) Ночной аудитор. Аудит
Ночной аудитор. Аудит Технология мультимедиа
Технология мультимедиа Программное обеспечение ПК
Программное обеспечение ПК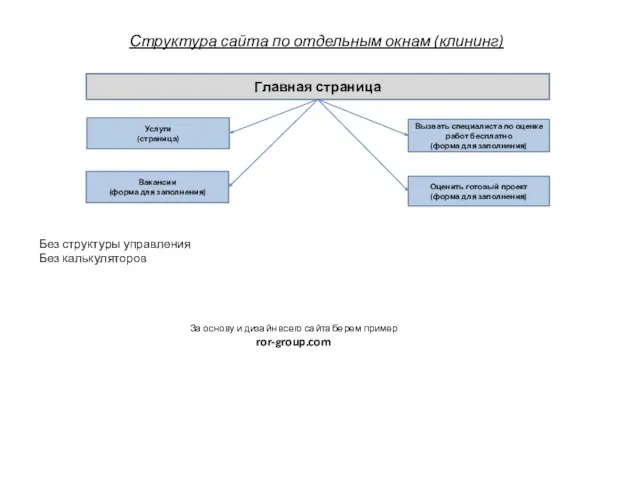 Структура сайта по отдельным окнам (клининг)
Структура сайта по отдельным окнам (клининг) Тестирование информационных систем
Тестирование информационных систем Защита информации
Защита информации Чек-листы и тест-кейсы
Чек-листы и тест-кейсы История развития вычислительной техники
История развития вычислительной техники Настройка динамической маршрутизации на базе протокола RIP на ободуровании MikroTik
Настройка динамической маршрутизации на базе протокола RIP на ободуровании MikroTik Кибербезопасность данных компаний
Кибербезопасность данных компаний Защита информации от утечки на объектах информатизации органов внутренних дел
Защита информации от утечки на объектах информатизации органов внутренних дел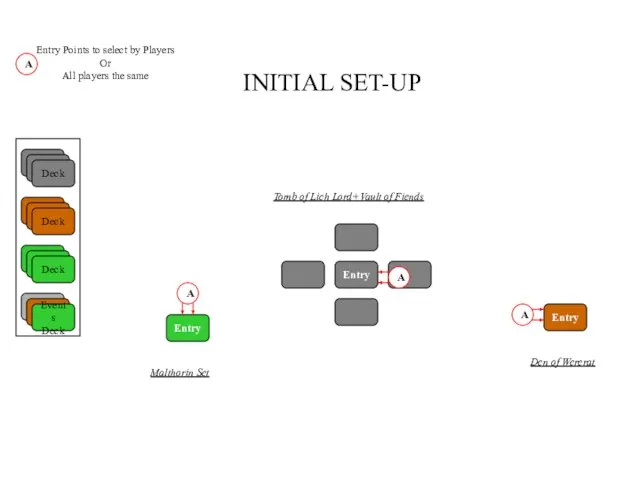 Initial SET-UP
Initial SET-UP