Технология программирования задач с циклами

Виды циклов
Общая характеристика операторов цикла
Счётный оператор цикла for
Оператор цикла с предусловием
Оператор цикла с постусловием
Типовые приемы программирования циклических процессов

for - оператор цикла
с параметром - счетчиком
(счетный оператор цикла)
(или арифметический оператор цикла).
while - оператор цикла
с предварительным условием (с предусловием);
do-while - оператор цикла
с последующим условием
(с постусловием);
В языке C++ имеется
три вида операторов цикла:

Оператор цикла for
применяется при заранее известном количестве повторений.
При этом некоторая переменная, называемая параметром цикла, должна последовательно принимать значения от начального до конечного.

Операторы цикла while и do -while
применяются в тех случаях, когда известно условие выполнения цикла,
а количество повторений может быть заранее не известно.

Счетный (арифметический) оператор цикла
и массивы.

1. Краткие теоретические сведения и программы с оператором for.
Цикл for организуется с помощью специальной переменной, которая называется параметром цикла.
Параметр цикла ‑ это числовая переменная, которая управляет работой цикла. Она изменяется по закону арифметической прогрессии, что обеспечивает повторение цикла нужное количество раз.

Параметры цикла
Для определения количества повторений заранее должны быть известны:
начальное значение параметра - tнач;
конечное значение параметра - tкон;
шаг изменения параметра - Δt.
Тогда количество повторений цикла определится по формуле:

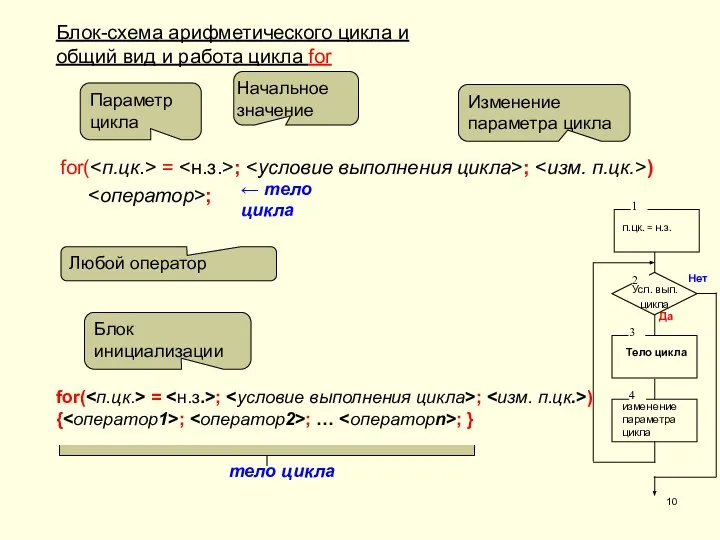
Структура цикла for на C++
имеет 4 блока, выполняющиеся в следующей последовательности:
- блок инициализации параметру цикла присваивается начальное значение;
- условие выхода из цикла (или, напротив - условие повторения цикла) - проверка параметра на конечное значение
- тело цикла основные действия, которые повторяются каждый раз, на каждом витке цикла;
- блок изменения параметра цикла на величину шага.

Блок-схема арифметического цикла и
общий вид и работа цикла for
for(<п.цк.> = <н.з.>; <условие выполнения цикла>; <изм. п.цк.>)
<оператор>;
Любой оператор
Параметр цикла
Начальное
значение
← тело цикла
Изменение
параметра цикла
for(<п.цк.> = <н.з.>; <условие выполнения цикла>; <изм. п.цк.>)
{<оператор1>; <оператор2>; … <операторn>; }
тело цикла
Блок инициализации

Пример 1. Допустим, что в группе из N человек собираются профсоюзные взносы по m рублей. Рассчитать, какую сумму группа перечислит в профсоюзный фонд.
#include
using namespace std;
int main()
{int N=20,m=100,s=0;
for(int i=1; i<=N; i++)
s+=m;
cout<< "Summa = "<
system("pause");
return 0;
}
Метод накопления суммы

2. Программа для определения
максимального элемента в массиве
Дано: массив (x1, x2, x3, … x10), xi = [± xx,xx].
Найти: номер и значение
максимального элемента массива.
Константа:
размер массива (кол-во эл-тов): n;
Входные величины:
массив x;
Параметр цикла: i;
Выходные величины:
номер максимального элемента: im
значение максимального элемента: x[im]

const int n=10;
double x[n];
cout << "enter " << n << " numbers\n";
for ( int i = 0; i < n; i++)
{
cout << "x[" << setw(2) << i << "]: ";
cin >> x[i];
}
cout << endl << "Massiv x " << endl;
for(int i = 0; i < n; i++)
cout << setw(4) << x[i];
cout << endl;
int im = 0;
for(int i = 1; i < n; i++)
if(x[i] > x[im])
im = i;
cout << "im = " << im << " x[im]= " << x[im] << endl;
-
1
2
2
-
+
3
3
4
-
+
-
5
5
6
-
+
-
7
-
-
8
-
-
9
-
-
ФРАГМЕНТ ПРОГРАММЫ: поиск минимакса по индексу

3. Программа для определения
первого по порядку следования элемента массива, значение которого равно заданной величине
Дано: целочисленный массив (f1, f2, f3, … f5),
заданное значение: h.
Найти: номер первого по порядку следования элемента со значением h.
Константа:
размер массива (кол-во эл-тов): n;
Входные величины:
массив f;
значение h.
Параметр цикла: i;
Выходные величины: номер искомого элемента: ih;
значение найденного элемента: f[ih].

const int n=5;
int f[n]; int h, ih=-1; //ih – это флаг
cout << "enter " << n << " numbers\n";
for ( int i=0; i
{ cout << "f[" << setw(2) << i << "]: ";
cin >> f[i]; }
cout << endl << "Massiv f " << endl;
for(int i=0; i
cout << setw(4) << f[i];
cout << endl;
cout << "h: "; cin >> h;
for(int i=0; i
if(f[i] == h)
{ ih = i;
break; }
if(ih != -1)
cout << "ih = " << ih << " h = " << h ;
else
cout << " No " ;
cout << endl;
0
-
-
1
-
-
2
+
2
Метод применения «флага»

4. Программа для определения
среднего арифметического
положительных элементов массива
Дано: массив (b1, b2, b3, … b6), bi = [± x,x].
Найти: среднее арифметическое положительных элементов массива.
Константа:
размер массива (кол-во эл-тов): n;
Входные величины:
массив b;
Параметр цикла: i;
Выходные величины:
кол-во полож. эл-тов: k;
ср. арифм. полож. эл-тов : s.

const int n=6;
double b[n];
cout << "enter " << n << " numbers\n";
for ( int i=0; i
{ cout << "b[" << setw(2) << i << "]: "; cin >> b[i]; }
cout << endl << "Massiv b " << endl;
for(int i = 0; i < n; i++) cout << setw(8) << b[i];
cout << endl;
int k=0; double s = 0; //счётчик k и накопитель суммы s
for(int i = 0; i < n; i++)
if(b[i] > 0)
{ s +=b[i];
k++; }
if(k != 0)
{ s = s / k;
cout << "k = " << k << " s = " << s ; }
else
cout << " No " ;
cout << endl;
-
0
-
-
+
1
2
1
-
2
-
-
+
3
6
2
-
4
-
-
+
5
12
3
Метод включения счётчика

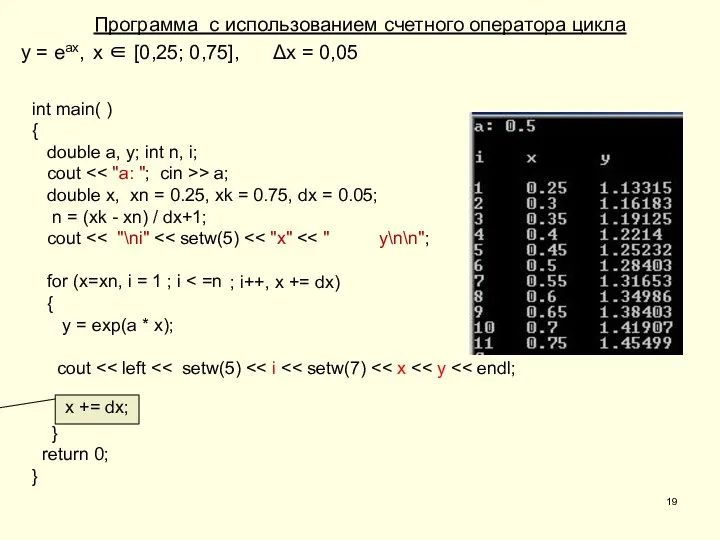
5. Пример программы
с использованием счетного оператора цикла
y = еах, х ∈ [0,25; 0,75], Δх = 0,05

Программа с использованием счетного оператора цикла
y = еах, х ∈ [0,25; 0,75], Δх = 0,05
int main( )
{
double a, y; int n, i;
cout << "a: "; cin >> a;
double x, xn = 0.25, xk = 0.75, dx = 0.05;
n = (xk - xn) / dx+1;
cout << "\ni" << setw(5) << "x" << " y\n\n";
for (x=xn, i = 1 ; i < =n ; i++ )
{
y = exp(a * x);
cout << left << setw(5) << i << setw(7) << x << y << endl;
}
return 0;
}
; i++, x += dx)
x += dx;

6. Параметр цикла вещественного типа
y = еах, х ∈ [0,25; 0,75], Δх = 0,05
#include
#include
#include
using namespace std;
int main( )
{
double a, y;
cout << "a: "; cin >> a;
double xn = 0.25, xk=0.75, dx=0.05;
for(double x = xn; x < = xk; x += dx)
{
y = exp(a * x);
cout << left << setw(7) << x << y << endl;
}
return 0;
}
Вещественные значения НЕЛЬЗЯ сравнивать на «равно»: в силу приближённого представления в цифровом ПК вещественных чисел.

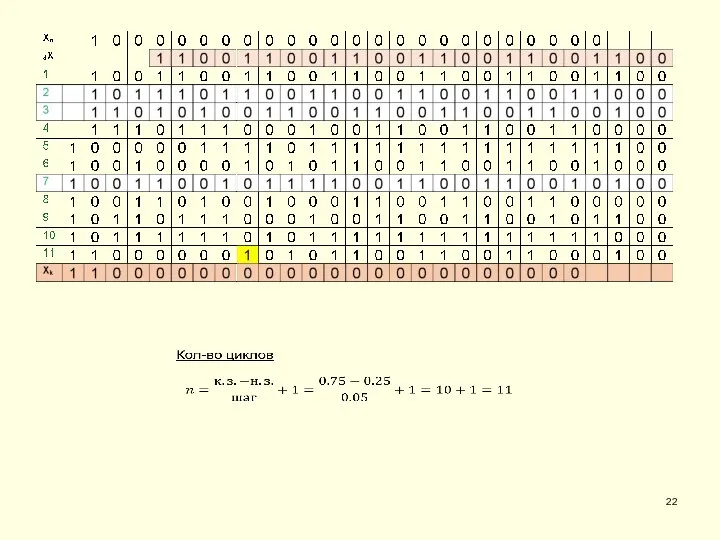
XN=0.2510=0.012=0.1⋅2-1
dX=0.0510=0.0000 1100 11002=0.(1100)⋅2-4
Xk=0.7510=0.112=0.11⋅20
Нормализованный экспоненциальный формат

6. Параметр цикла вещественного типа
y = еах, х ∈ [0,25; 0,75], Δх = 0,05
#include
#include
#include
using namespace std;
int main( )
{
double a, y;
cout << "a: "; cin >> a;
double xn = 0.25, xk=0.75, dx=0.05;
for(double x = xn; x < xk + dx/2; x += dx)
{
y = exp(a * x);
cout << left << setw(7) << x << y << endl;
}
return 0;
}

7. Использование нескольких переменных управления циклом
Цикл for является одним из наиболее гибких операторов, т.к. допускает большое кол-во разнообразных вариантов.
Например, допустимо использовать несколько переменных управления.
Пример:
for (x = 0, y = 10; x <= y; ++x, --y)
cout << x << ' ' << y <<'\n';

8. Пропущенные секции в операторе for
Пример (отсутствует секция приращения):
Цикл, который должен выполняться до тех пор, пока с клавиатуры не будет введено число 123.
int x;
for (x = 0; x != 123; )
{
cout << "enter number: ";
cin >> x;
}

Пример (отсутствуют секции инициализации и приращения):
x = 0;
for ( ; x < 10; )
{
cout << x << ' ';
x++;
}

Пример (отсутствуют все секции – бесконечный цикл):
for ( ; ; )
{
// …
}
Для выхода из такого цикла необходимо в теле цикла использовать оператор break, размещенный внутри условного оператора if.
Например: кроты запасли в своей норке S штук зерен. С определенной периодичностью они обновляют запасы своих норок ds1= a | sin (3t+2) | и поедают их с величиной ds2 = 5⋅103. Хитрые же мыши с другой периодичностью иногда обворовывают, а иногда и возвращают награбленное у кротов на величину
ds3 = b (sin (5t-4) ). Запустить процесс заполнения/опустошения норки.
double s=2.3e20; int t=0; float a=35,b=52;
for ( ; ; )
{t++; ds1 = a*abs(sin(3*t)+2; ds2=5e3 ; ds3 = b *(sin (5t-4));
s+=ds1-ds2- ds3;
}
If (s<=0) break;

Пример (отсутствует тело цикла):
(бестелесые циклы весьма полезны)
int i;
int sum = 0;
// суммирование чисел от 1 до 10
for ( i = 1 ; i <= 10 ; sum += i++ ) ; // цикл без тела цикла
Чтобы понять смысл оператора sum += i++ (это обычная запись для C++)
необходимо разобрать его на составные части:
sum = sum + i;
i = i + 1;

2.3 Табулирование функции счетным оператором

Словесный алгоритм задачи

Решение задачи
#include
#include
using namespace std;
int main()
{
float xn, xk, dx, t , y;
printf("Enter xn, xk, dx,t \n");// \n -переход на новую
// строку = endl
cin>>xn>>xk>>dx>>t;
for (float x=xn;x<=xk;x+=dx)
{
if(x<0) y=t;
else if (x>=0 && x<10) y=t*x;
else y=2*t;
if (t>100) printf("%9.2f %9d \n", x,(int)y);
else printf("%9.2f %9.2f \n", x, y);
}
system("pause");
return 0;
}

Замечание о внутренних переменных
Переменная х описана ВНУТРИ цикла, после его завершения, переменная х УДАЛЯЕТСЯ из памяти и мы не можем получить доступ к ее значению!!!
Область видимости этой переменной – только тело оператора for.

Операторы цикла while и do -while
применяются в тех случаях, когда известно условие выполнения цикла,
а количество повторений может быть заранее не известно.

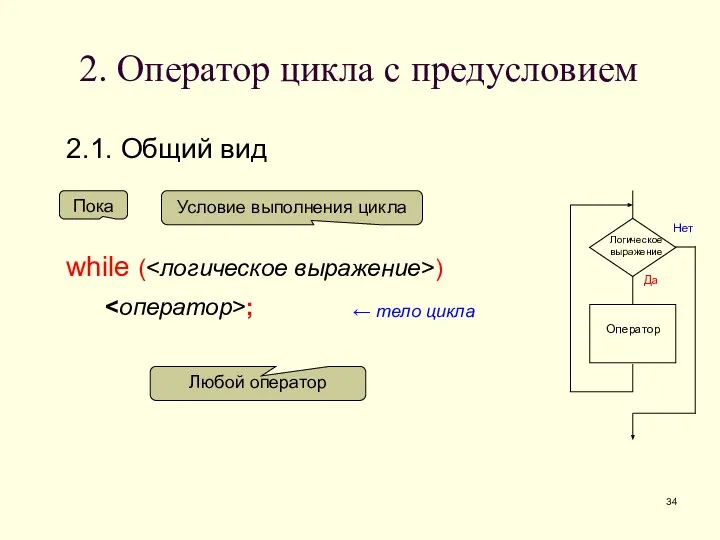
2. Оператор цикла с предусловием
2.1. Общий вид
while (<логическое выражение>)
<оператор>;
Любой оператор
Пока
Условие выполнения цикла
← тело цикла

Пример 1. Автомобиль движется со скоростью 5 км/ч и начинает наращивать скорость с ускорением 10 км/ч2 до тех пор пока не будет достигнута скорость 60 км/час. Определить, за какое время эта скорость будет достигнута.

#include
using namespace std;
int main()
{int speed = 5, time = 0, count=0;
while ( speed < 60 )
{
cout << count <<"-speed = " << speed << " time= "<
speed += 10; // приращение скорости
count++; // подсчёт повторений цикла
time++;// наращивание времени
}
cout<< "final speed "<
system("pause"); return 0;}

Анализ программы
инициализация трёх переменных (скорости speed, времени time и счётчика цикла count реализуется до начала цикла;
условие speed < 60 определяет возможность выполнения цикла, и пока скорость остаётся меньше 60, условие истинно и скорость будет нарщиваться;
управление условием реализуется оператором speed += 10;
тело цикла составляют операторы вывода на консоль и операторы приращения счётчика и времени.

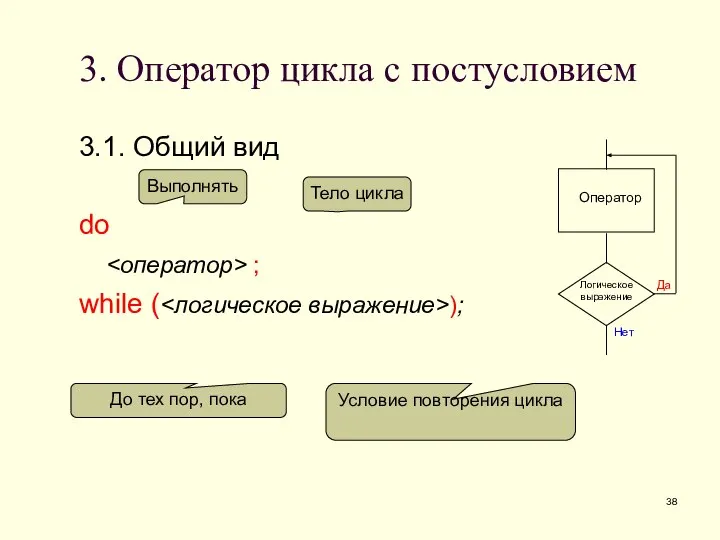
3. Оператор цикла с постусловием
3.1. Общий вид
do
<оператор> ;
while (<логическое выражение>);
Выполнять
До тех пор, пока
Условие повторения цикла
Тело цикла

3.2. Технология программирования задачи с оператором цикла do-while
Составить программу:
Вычислить с заданной точностью сумму членов
бесконечного ряда:
Условие прекращения вычислений
Sn - Sn-1 = < δ − малое число больше нуля.
Выбор идентификаторов:
Входной Параметр цикла Выходной
δ → d, n → n, S → s

int main( )
{
cout << "d: ";
double d;
cin >> d; double s = 0;
double n = 1;
do
{
s += 1 / n;
n ++;
} while (1 / n > d);
cout << "n = " << n << " s = " << s << endl;
}
Sn - Sn-1 = < δ
0
+ 1/1
+ 1/2
+ 1/3
1
+ 1
+ 1
+ 1
1
2
3
4
1
0.5
0.3333
0.25
1.0000
1.5000
1.8333
// Заголовок функции
// Начало кода функции
// Вывод ответа
0
0,3
1.8333

Применение рекуррентных соотношений для программирования рядов
Вычислить сумму бесконечного ряда с заданной точностью (суммировать до тех пор, пока модуль текущего элемента ряда не станет меньше заданной точности) двумя способами:
1) по общей формуле ряда;
2) по рекуррентной формуле.

Первый способ: применяем формулу общего члена
Входные параметры:
eps – точность вычислений ε
R – значение первого элемента ряда при начальном значении k – номере 1-го элемента ряда
Промежуточные параметры
P1 – интегратор для накопления произведения (k+1)!
P2 – интегратор для накопления произведения (2*k+1)!
k – номер итерации, совпадает с номером элемента ряда R – текущий (k‑ый) элемент ряда.

Выходные параметры
S – сумма элементов ряда
Определение начальных значений переменных
Для переменной k начальное значение дано:
k = 0 Подставим начальное значение k в формулу ряда
получим начальное значение переменной R:
Принимаем начальное значение сумматора
S = 0, начальные значения интеграторов
P1 = 1, P2 = 1.

Контрольный пример:
пусть ε=0,1:
k = 1; P1 = 1⋅2; P2 = 1⋅2⋅3;
R = ‑ 0.333 > ε; S = 0.667;
k = 2; P1 = 1⋅2⋅3; P2 = 1⋅2⋅3⋅4⋅5;
R = +0.05 < ε; S = 0.687;
Выход из цикла.
Ответ: S = 0.687

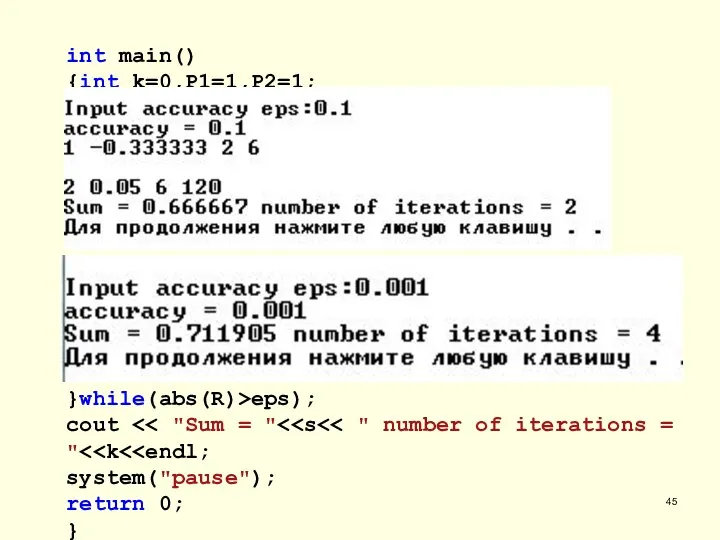
int main()
{int k=0,P1=1,P2=1;
float R=1, s=0, eps;
cout<<"\nInput accuracy eps:"; cin>>eps;
cout<<"accuracy = "<
do
{s+=R;
k=k+1;
P1*=(k+1);
P2*=(2*k)*(2*k+1);
R=pow(-1.,k)*(float)P1/float(P2);
cout<<'\n'< ' <
}while(abs(R)>eps);
cout << "Sum = "<
return 0;
}

nan – not a number
k R P1 P2
k R P1 P2

Анализ программы
Анализ решения показывает, что программа работает верно, т.к. результаты программы совпадают с контрольным примером.
Для проверки полноты программы, получено решение и для другого значения точности.
Анализ программы позволяет выяснить её неэффективность:
Возведение в степень ‑1 неоправданно при большом количестве итераций, т.к. результат всегда будет или +1 или ‑1.
Накопление произведения для вычисления двух факториалов тоже неэффективно, поскольку при большом количестве итераций будет приводить к недопустимо большим числам в числителе и знаменателе.
При вычислении R используются операторы приведения типа (от целого к вещественному) для того, чтобы, во-первых, избежать целочисленного деления, и, во-вторых, чтобы не было лишних предупреждений от транслятора.

Оценка времени выполнения процесса
Если нужно замерить время выполнения фрагмента кода на С++, используется clock() из модуля ctime — она возвращает число таков, измеряемое процессором от начала выполнения программы.
Глобальная константа CLOCKS_PER_SEC хранит число тактов, выполняемое процессором в секунду. Соответственно, чтобы получить время работы программы в секундах достаточно результат работы функции разделить на эту константу:
clock() / CLOCKS_PER_SEC;
Для определения времени работы фрагмента программы нужно определить моменты времени до фрагмента и после него, а затем — посчитать разницу.
#include
// ...
unsigned int start_time = clock(); // начальное время
// здесь должен быть фрагмент кода, время выполнения которого нужно измерить
unsigned int end_time = clock(); // конечное время
unsigned int search_time = (end_time - start_time)/CLOCKS_PER_SEC; // искомое время

Код с операторами оценки времени
clock_t begin = clock();
/* here, do your time-consuming job */
do
{
s += R;
k = k + 1;
P1 *= (k + 1);
P2 *= (2 * k)*(2 * k + 1);
R = pow(-1., k)*(float)P1 / float(P2);
cout << k << ' ' << R << ' ' << P1 << ' ' << P2 << endl;
} while (abs(R) > eps);
cout << "Sum = " << s << " number of iterations = " << k << endl;
clock_t end = clock();
double time_spent = (double)(end - begin) / CLOCKS_PER_SEC;
cout << "Time spent = " << time_spent << endl;
Переменная begin класса clock_t

Второй способ
Для начала выведем рекуррентную формулу, т.е. соотношение, которое позволяет получать любой k-й член через (k-1)-й:
Вычислим значение коэффициента Q для нашего ряда:
ТАКОЙ СПОСОБ НЕОБХОДИМ ТОЛЬКО В СЛУЧАЯХ НЕОЧЕВИДНОЙ СВЯЗИ МЕЖДУ n-м И (n-1)-м членами. ОБЫЧНО РЕКУРРЕНТНЫЕ ОТНОШЕНИЯ НАХОДЯТСЯ БОЛЕЕ ПРОСТЫМ МЕТОДОМ ПОДБОРА

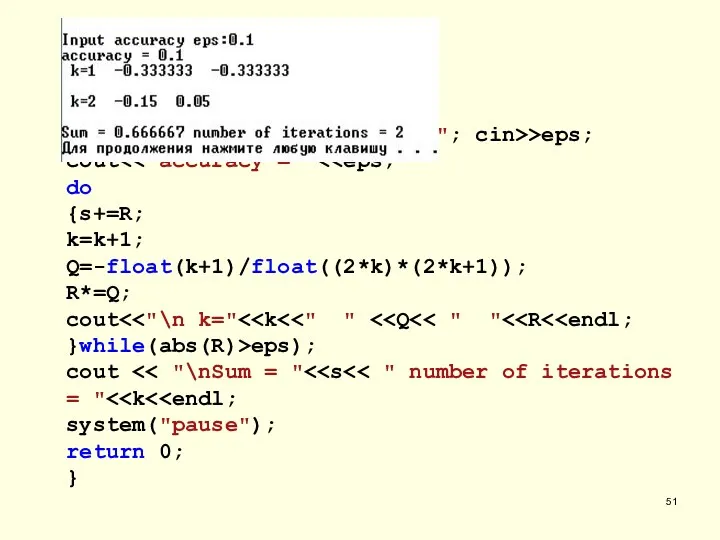
int main()
{int k=0;
float Q, R=1, s=0, eps;
cout<<"\nInput accuracy eps:"; cin>>eps;
cout<<"accuracy = "<
do
{s+=R;
k=k+1;
Q=-float(k+1)/float((2*k)*(2*k+1));
R*=Q;
cout<<"\n k="<
}while(abs(R)>eps);
cout << "\nSum = "<
return 0;
}

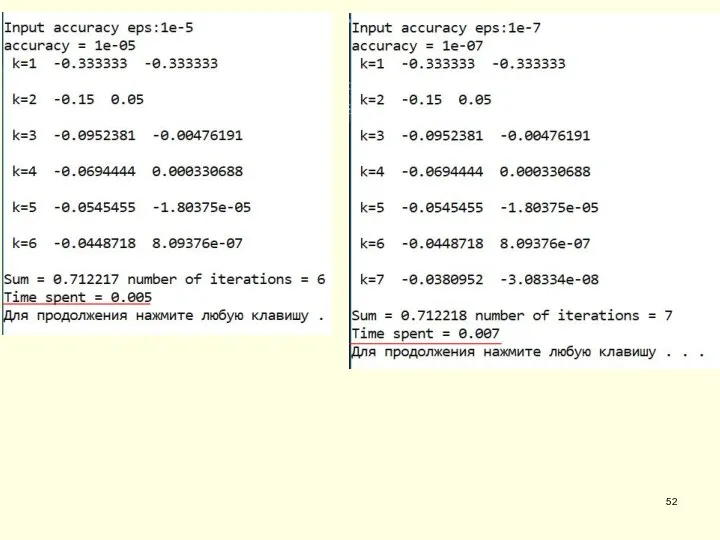
Анализ программы
Преимущества этого метода очевидны: нет необходимости в неоправданно больших умножениях, бессмысленном возведении в степень (‑1), этот алгоритм требует меньше процессорного времени.

Генерация псевдослучайных чисел средствами языка С++

Функции работы со случайными числами
Случайные числа на языке программирования С++ могут быть сгенерированы функцией rand() из стандартной библиотеки cstdlib.
Функция rand() генерирует числа в диапазоне от 0 до RAND_MAX.
RAND_MAX — это константа, определённая в библиотеке
.
Для Microsoft Visual Studio: RAND_MAX = 32767, но оно может быть и больше, в зависимости от компилятора.

Чтобы функция rand() всегда возвращала разные числа, её нужно использовать в паре с функцией srand(unsigned int арг). Аргумент арг задаёт то стартовое число, на базе которого и создаётся база случайных чисел.
Для того, чтобы автоматически всегда брать разные стартовые числа, рекомендуется использовать функцию
(unsigned int) time( NULL)
которая возвращает число секунд, прошедших с 00:00:00 UTC 1 января 1970 года (Unix-время равно нулю).
Функции работы со случайными числами

Особенности работы функции srand()
Чаще всего в качестве передаваемой величины в функцию srand() используют системное время в секундах, т.к. это число будет всегда разным, а соответственно, мы будем получать на выходе из rand() разные случайные числа.
Чтобы передать в функцию srand() текущее системное время, можно использовать библиотечную функцию time(), описанную в библиотеке
.
Для того, чтобы эта функция возвращала текущее время в секундах (секунды отсчитываются от 00:00:00), нужно вызывать ее с параметром NULL: srand(time(NULL)); или srand(time(0));.
Если нет необходимости в формировании всегда разных случайных чисел, то функцию srand можно задать с любой константой или вовсе не включать её в программу.

Пример 1. Инициализация массива случайными числами в заданном диапазоне значений: от -10 до 10.
tf[i] = rand( ) % (r_max - r_min+1) + r_min;

#include
#include
using namespace std;
// функция инициализации массива случайными числами
int main()
{
int tf [10], nf, r_min, r_max;
nf = 10;
cout<< “Inpiut min and max limit values:”; cin>>r_min>>r_max;
srand( (unsigned int) time( NULL ) ); // рандомизация генератора
for (int i = 0; i < nf; i++ ) // n - количество чисел
tf[i] = rand( ) % (r_max - r_min+1) + r_min; // формирование случайного числа
for (int i = 0; i < nf; i++ ) cout<<'\t'<< tf[i]; cout<
return 0;
}
Функция rand генерирует случайные числа, возвращает псевдослучайное целое число в диапазоне от 0 до RAND_MAX.
RAND_MAX это константа, определенная в
. По умолчанию её значение может изменяться, в зависимости от реализации, но, как правило, макрос RAND_MAX меньше значения 32767 не бывает.
Создание базы случайных чисел на основе Time (NULL)

Пример 1. Определить количество цифр в числе N, заданным случайным образом.
#include
#include
#include
using namespace std;
int main()
{int Number,M,N, count;
srand(10);
cout<< " What is the maximal value of the Number?";
cin>>M;
N=rand()%M;
Number=N;

// Метод - цикл с делением
count = (Number == 0) ? 1 : 0;
while (Number != 0)
{
count++;
Number /= 10;
}
cout<<"\nCounts of digits in the number "<

// Метод - десятичный логарифм и округление
// хорош для очень больших чисел.
N=rand()%M;
Number=N;
count=(Number == 0) ? 1 : (int)ceil(log10(abs(Number) + 0.5));
cout<<"\nCounts of digits in the number "<
system("pause");
return 0;
}

Пример 2. Паук находится на плоскости в точке с координатами x=50 и y=50. Каждую секунду он делает шаг влево, вправо, вниз или вверх с равной вероятностью. Смоделируйте движение паука с помощью генератора случайных чисел.
Координаты x(t) и y(t) сохраните в одномерных массивах. Напечатайте траекторию паука в виде таблицы, которая содержит в клеточке с координатами x и y символ “.”, если там паук не был, “+”, если паук там побывал 1 раз, “*”- для двух раз, “#” - для трёх и символ “@” -, если он побывал больше раз.

Блок инициализации
#include
#include
#include
using namespace std;
int main()
{
cout << " Случайное блужданиепо плоскости." << endl;
const int N=61, K=1550, J=1;
char buf[N+1]; ];// массив символов ~ количество посещений
int xy[N][N];// массив для хранения количества посещений клетки N,N
int x=N/2;// ставим курсор в середину консоли
int y=N/2;

// Заполнение двумерного массива значениями при
// моделировании движения паука
for(int m=0; m m++)
for(int n=0; n
xy[m][n]=0;
xy[x][y]=1;
// запись координат движения паука в массив
for(int k=1; k
{
for(int j=0; j
x+=rand()%3-1;//формирование сл.чисел от -1 до 1
for(int j=0; j
y+=rand()%3-1;

//проверка выхода к границам
if(x<0)x=0;
if(x>N-1)x=N-1;
if(y<0)y=0;
if(y>N-1)y=N-1;
xy[x][y]+=1; // отметка о посещении точки в массиве
}

// Заполнение символьного массива
for(int m=0; m
{
for(int n=0; n
switch(xy[m][n])
{
case 0: buf[n]='.'; break;
case 1: buf[n]='+'; break;
case 2: buf[n]='*'; break;
case 3: buf[n]='#'; break;
default: buf[n]='@';
}
buf[N]='\0';// ставим конец строки

// Выводим символьный массив на консоль
cout << buf << endl;
}
cout<< endl;
system("pause");
return 0;
}

Краткие итоги
Оператор for на С++ состоит из четырёх секций: инициализации, условия, тела цикла, приращение. Любая из секций может быть опущена с соблюдением синтаксиса, позволяя гибко строить алгоритм, используя этот компактный и многофункциональный оператор.
Условные операторы while и do-while по эффективности эквиваленты оператору for, удобны при описании условных алгоритмов.
Оператор for необходим при работе с элементами массивов, при вычислении сумм конечных рядов, при любых алгоритмах, где используется счётчик при заранее известном количестве итераций.
При алгоритмизации задач с бесконечными рядами можно использовать любые типы циклов, однако while и do-while многими полагаются как более наглядные.
Рекуррентные формулы при вычислении сумм длинных рядов не только позволяют избегать операций прерывания, но и существенно экономят процессорное время.
Для оценки времени удобно пользоваться функций clock.
Формула для формирования числа в заданном диапазоне значений
tf[i] = rand( ) % (r_max - r_min+1) + r_min;