Содержание
- 2. Структурирование Структурирование – совокупность технологий программирования, приемов и закономерностей, используемых при создании программного продукта Как написать
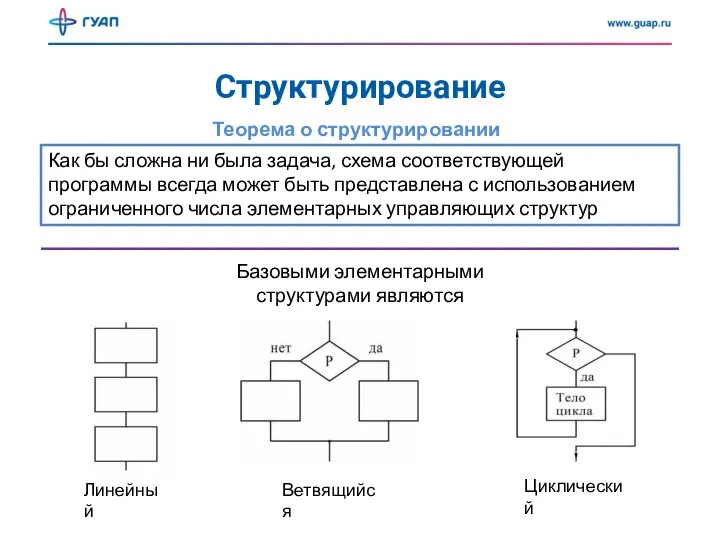
- 3. Структурирование Теорема о структурировании Как бы сложна ни была задача, схема соответствующей программы всегда может быть
- 4. Структурирование Какова бы ни была степень и глубина «вложенности», важно, что любая конструкция в конечном итоге
- 5. Структурирование Существует три основные технологии структурирования Нисходящая Восходящая Комбинированная Нисходящая Задачи разбиваются на подзадачи, которые можно
- 6. Структурирование Восходящая Общий алгоритм неясен, но известно решение отдельных алгоритмов и задач, то можно начинать проектирование
- 7. Структурирование Последовательность действий при структурировании: Попытка решения задачи за один шаг. Если на этом шаге появляется
- 8. Структурирование Структурирование позволяет Не пропустить ни одного шага. Сделать большой шаг, пропустив часть предписаний. Предотвращается появление
- 9. Структурирование Пример Задача: дана последовательность, содержащая от 2 до m слов (m>=2), в каждом из которых
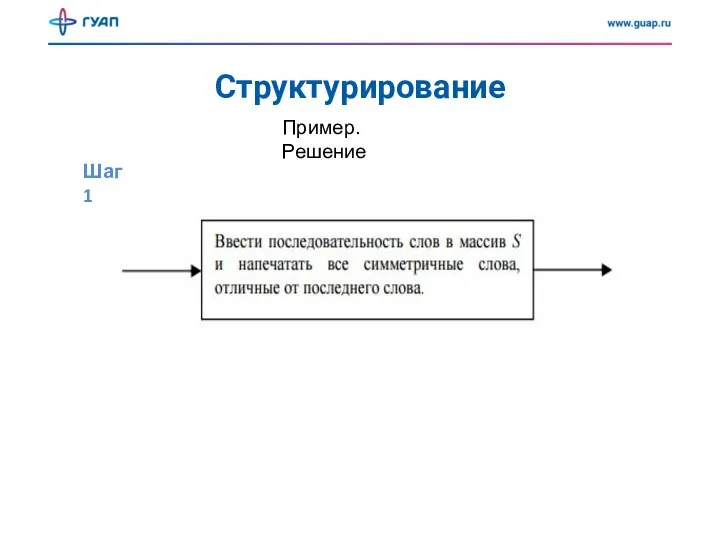
- 10. Структурирование Шаг 1 Пример. Решение
- 11. Структурирование Шаг 2 Пример. Решение Решение задачи разбивается на два последовательных блока: ввести данные в массив;
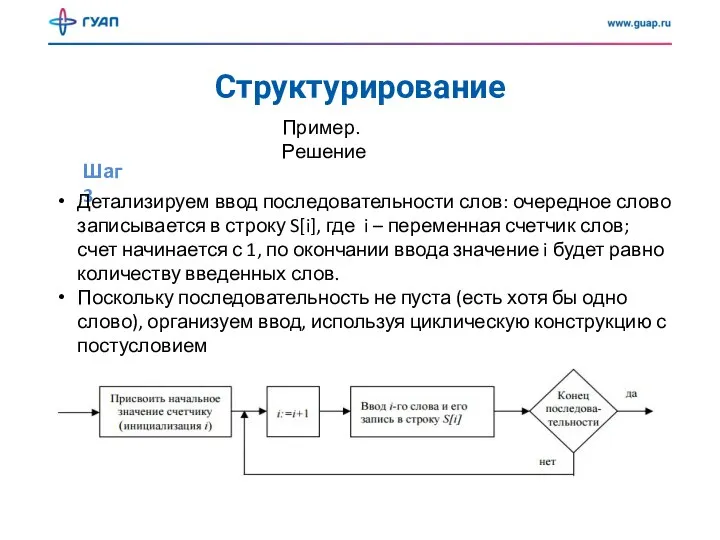
- 12. Структурирование Шаг 3 Пример. Решение Детализируем ввод последовательности слов: очередное слово записывается в строку S[i], где
- 13. Структурирование Шаг 4 Пример. Решение Уточним блоки, входящие в конструкцию, полученную на Шаге 3. Для того,
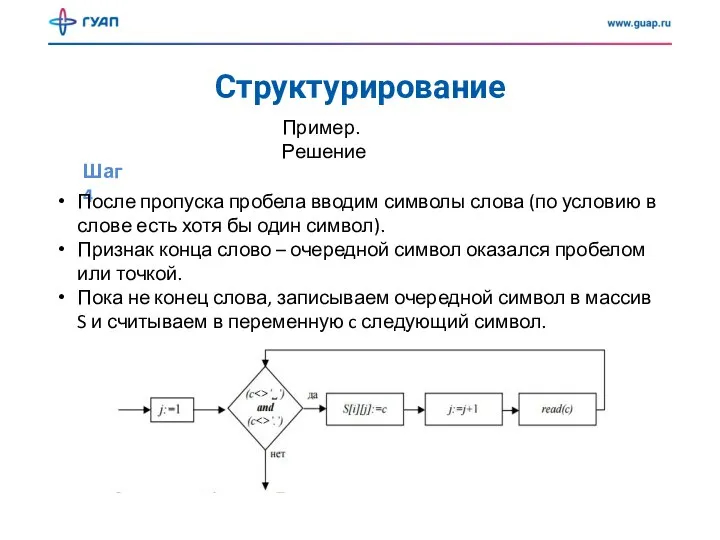
- 14. Структурирование Шаг 4 Пример. Решение После пропуска пробела вводим символы слова (по условию в слове есть
- 15. Методы построения алгоритмов Этапы построения алгоритмов Задача коммивояжера Коммивояжеру для совершения торговых сделок требуется объехать n
- 16. Методы построения алгоритмов Дополнительные условия и допущения: Используемое понятие стоимости должно быть формализовано Для каждой пары
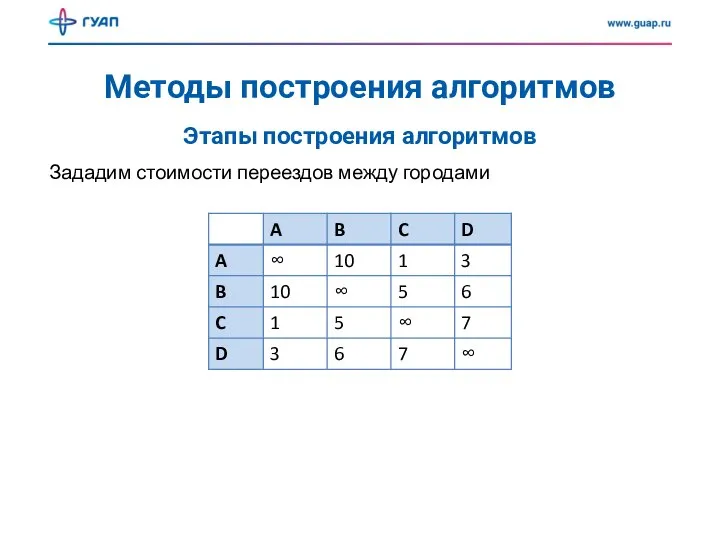
- 17. Методы построения алгоритмов Зададим стоимости переездов между городами Этапы построения алгоритмов
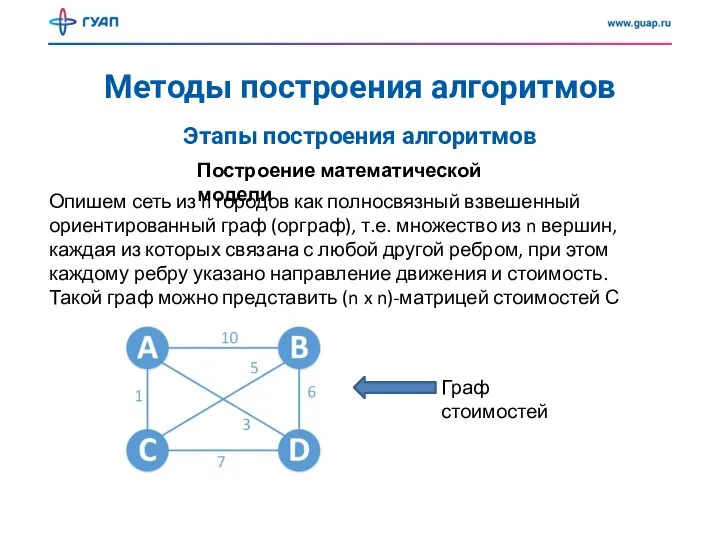
- 18. Методы построения алгоритмов Построение математической модели Этапы построения алгоритмов Опишем сеть из n городов как полносвязный
- 19. Методы построения алгоритмов Построение математической модели Этапы построения алгоритмов Пронумеровав города от 1 до n, можно
- 20. Методы построения алгоритмов Выбор или построение алгоритма Этапы построения алгоритмов Наиболее очевидный и прямой метод –
- 21. Методы построения алгоритмов Проверка корректности алгоритма Этапы построения алгоритмов Для любого предложенного алгоритма должно быть доказано,
- 22. Методы построения алгоритмов Анализ сложности алгоритма Этапы построения алгоритмов В нашей задаче всего существует (n-1)! Маршрутов,
- 23. Методы построения алгоритмов Реализация алгоритма Этапы построения алгоритмов Как правило алгоритм может быть реализован различными способами.
- 24. Методы построения алгоритмов Проверка корректности программы Этапы построения алгоритмов Или тестирование, является самостоятельной большой задачей. На
- 25. Методы построения алгоритмов Оценка сложности программы Этапы построения алгоритмов Время выполнения программы, занимаемая программой память не
- 27. Скачать презентацию


















 Как написать сообщение в соцсетях, чтобы оно было интересным
Как написать сообщение в соцсетях, чтобы оно было интересным Разработка eSIM
Разработка eSIM Информация и её свойства. Информация и информационные процессы
Информация и её свойства. Информация и информационные процессы Технологии Smart, KPI, TO
Технологии Smart, KPI, TO Понятие тега HTML
Понятие тега HTML Техника безопасности и правила поведения при работе в компьютерном классе
Техника безопасности и правила поведения при работе в компьютерном классе Поиск клиентов и планирование доходов. Инфопродюсер
Поиск клиентов и планирование доходов. Инфопродюсер Способы записи алгоритмов
Способы записи алгоритмов Ближе к клиенту
Ближе к клиенту Правила оформления скриншота
Правила оформления скриншота _Р 2.Т 2.4 Передача ИНФ
_Р 2.Т 2.4 Передача ИНФ Поведенческая реклама, ретаргетинг
Поведенческая реклама, ретаргетинг Особенности SQL применительно к СУБД MySQL
Особенности SQL применительно к СУБД MySQL Логические элементы компьютера
Логические элементы компьютера Система компьютерного моделирования процессов Полигон
Система компьютерного моделирования процессов Полигон Информационно-коммуникативные технологии в начальной школе
Информационно-коммуникативные технологии в начальной школе Dates. Round
Dates. Round Цикловое управление манипулятором МП-9с c помощью TM-238
Цикловое управление манипулятором МП-9с c помощью TM-238 Беседа. Правила безопасности в интернете
Беседа. Правила безопасности в интернете Образ Северной Кореи в российских СМИ
Образ Северной Кореи в российских СМИ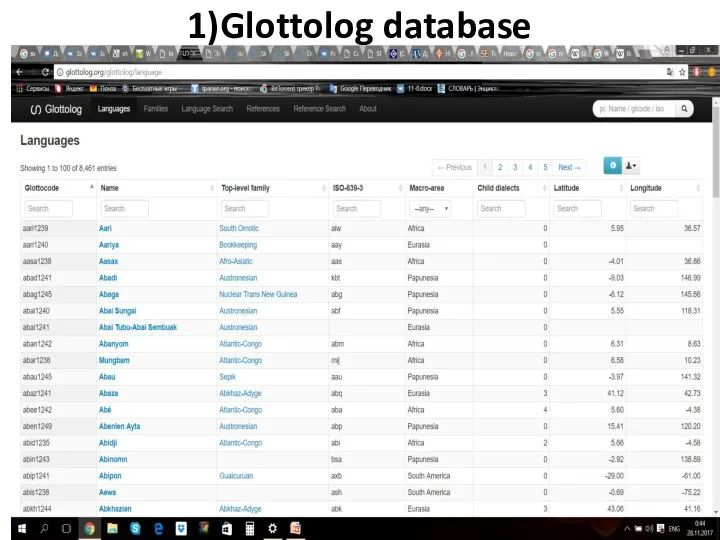 Glottolog-Всесторонняя справочная информация для языков мира
Glottolog-Всесторонняя справочная информация для языков мира Представление данных и машинные операции
Представление данных и машинные операции Untitled presentation (2)
Untitled presentation (2) Презентация на тему Основы логики
Презентация на тему Основы логики  Архивация и разархивация файлов
Архивация и разархивация файлов Правило возведения в степень
Правило возведения в степень Python-Массивы (списки)
Python-Массивы (списки) Параллельное программирование в стандарте OpenMP
Параллельное программирование в стандарте OpenMP