графе”, Вестн. С.-Петербург. ун-та. Сер. 10. Прикл. матем. Информ. Проц. упр., 2015, № 2, 61–76.
В. В. Гусев, Ситуация равновесия в игре патрулирования с камерой слежения // Труды Карельского научного центра РАН, № 10. 2015. С. 28-33. DOI: 10.17076/mat145.
В. В. Гусев, Поиск оптимального начального распределения местоположения игроков в игре патрулирования //Вестник Удмуртского университета. Математика. Механика. Компьютерные науки, 2015, т. 25, вып. 4, с. 453-458 DOI: 10.20537/vm150402.
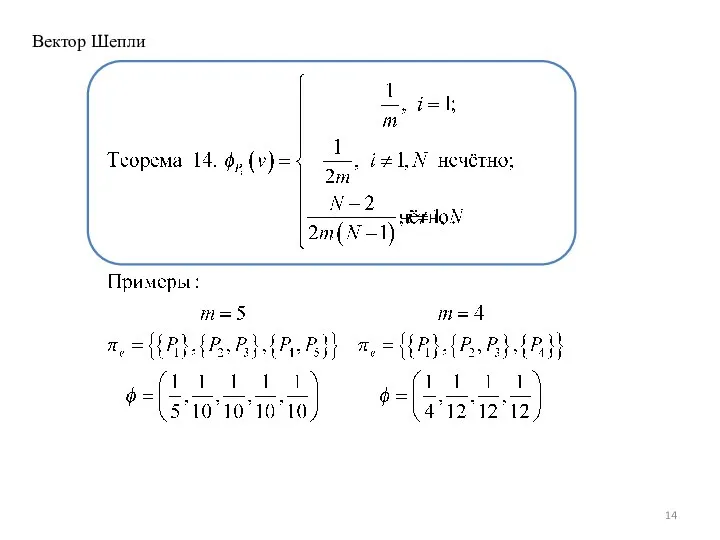
В. В. Гусев, “Векторы Шепли, Оуэна и Ауманна–Дрезе в игре патрулирования с коалиционной структурой”, МТИП, 8:4 (2016), 30–42.
Список публикаций ВАК по теме диссертации















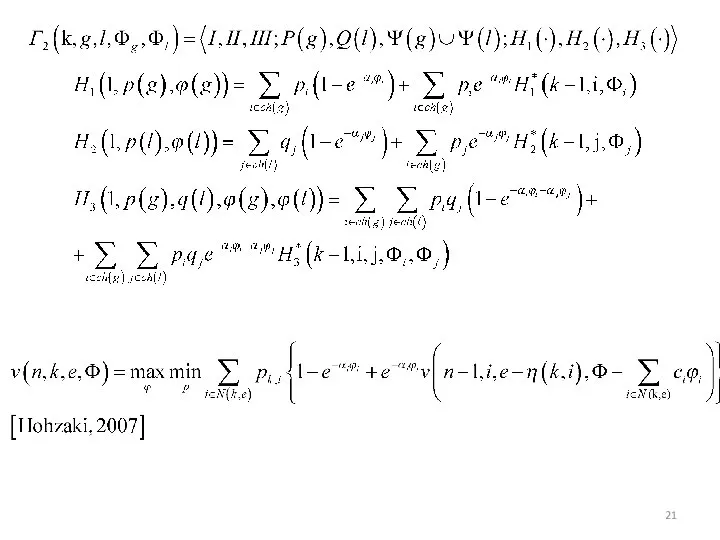

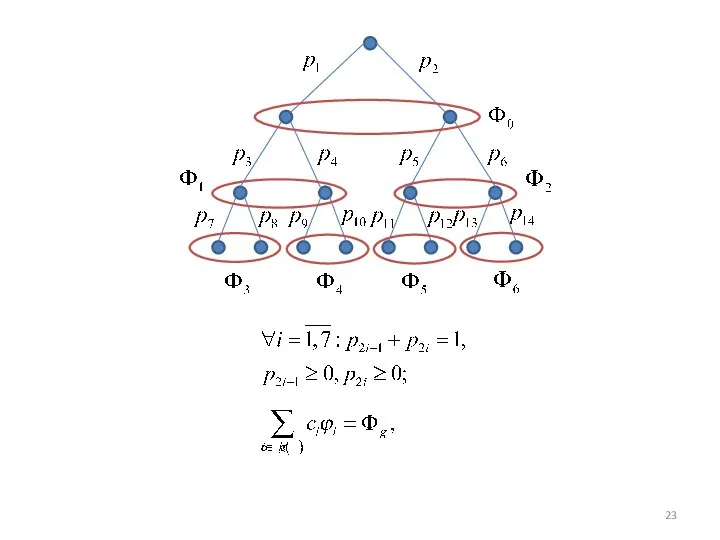







 Pascal ABC. Работа с числовыми данными. Целые числа. Урок 3-4
Pascal ABC. Работа с числовыми данными. Целые числа. Урок 3-4 Описание разработки. Алгоритм. Блок-схема
Описание разработки. Алгоритм. Блок-схема Стандарты. Занесение данных в информационные системы ТМ
Стандарты. Занесение данных в информационные системы ТМ Виды кабелей для передачи информации
Виды кабелей для передачи информации Вариации по мотивам… Новые задания с развернутым ответом №25 и №26
Вариации по мотивам… Новые задания с развернутым ответом №25 и №26 Презентация на тему Операционные системы, среды и оболочки
Презентация на тему Операционные системы, среды и оболочки  Загальні відомості про інтерфейс
Загальні відомості про інтерфейс Введение в CSS. Блочная верстка.. Занятие 2
Введение в CSS. Блочная верстка.. Занятие 2 Триггеры в презентации. Создание слайдов с триггерами
Триггеры в презентации. Создание слайдов с триггерами Мультимедиа в Театральном музее
Мультимедиа в Театральном музее Massenmedien: Fernsehen
Massenmedien: Fernsehen Алгоритм получения доступа к Электронному дневнику
Алгоритм получения доступа к Электронному дневнику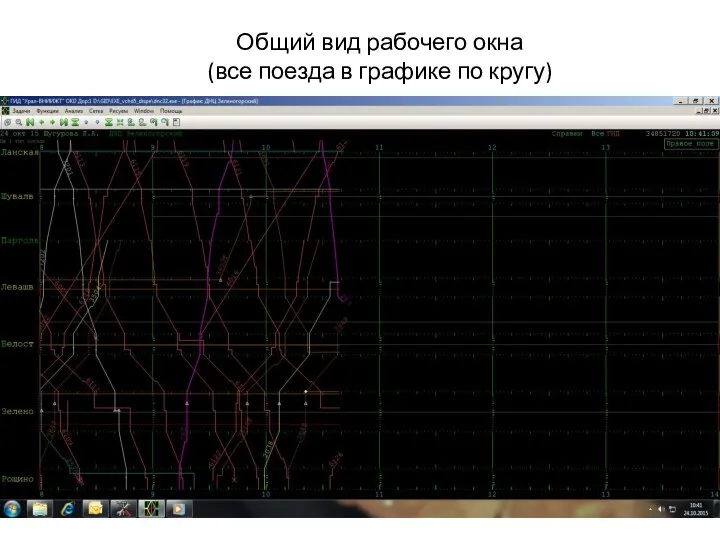 Общий вид рабочего окна (все поезда в графике по кругу)
Общий вид рабочего окна (все поезда в графике по кругу) Лекция 3 Вычислительные машины
Лекция 3 Вычислительные машины Я сдаю. Сдавайте и снимайте жильё посуточно через Безопасную сделку
Я сдаю. Сдавайте и снимайте жильё посуточно через Безопасную сделку 70 лет Победы. Основные цели информационного сопровождения
70 лет Победы. Основные цели информационного сопровождения База данных Справочник отелей города
База данных Справочник отелей города Лекция 6
Лекция 6 Рассылки
Рассылки Базы данных
Базы данных Устройство компьютера
Устройство компьютера Самая популярная газета в Сан-Фиерро
Самая популярная газета в Сан-Фиерро Роль средств массовой информации
Роль средств массовой информации Базовая обработка изображений на компьютере
Базовая обработка изображений на компьютере Создание красивых картинок в фотошопе
Создание красивых картинок в фотошопе Рынок ценных бумаг и интернет
Рынок ценных бумаг и интернет Диаграммы сущность – связь
Диаграммы сущность – связь Практическое задание Криптография
Практическое задание Криптография