Нелинейная детерминированная система

Структура курса
Принципы моделирования: аналогия, изоморфизм, гомоморфизм, системный подход. Моделирование нелинейной динамической системы. Метод Монте-Карло. Моделирование случайных чисел и величин
Дискретизация по времени и частоте. Теорема Котельникова. Представления в ортогональных базисах. Преобразование Фурье. Моделирование синусоиды. Моделирование элементов речевых сигналов
Моделирование процессов. Белый шум, винеровский процесс, низкочастотный случайный процесс
Автоматы. Кодеры. Декодеры
Стохастические автоматы. Моделирование систем массового обслуживания. Очереди
Технология моделирования. Основные этапы моделирования. Компьютерный эксперимент. Факторы. Отклики. Анализ результатов эксперимента.
Верификация элементов моделей. Случайные процессы, случайные величины
Разработка моделей по заданному аналитическому описанию

Нелинейная детерминированная система
Визуализация
Режимы
Оценка точек ρ, в которых меняется режим
Оценка точек стационарности

Моделирование случайных чисел
Генератор
равномерно распределенных случайных величин
Генератор
нормально распределенных случайных величин
Эмпирическая оценка плотности вероятности
Визуализация
Аналитическое выражение p(r)

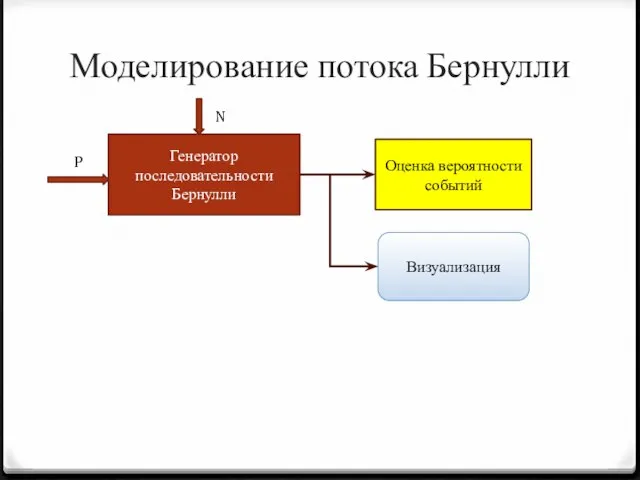
Моделирование потока Бернулли
Генератор последовательности Бернулли
Оценка вероятности событий
Визуализация
P
N

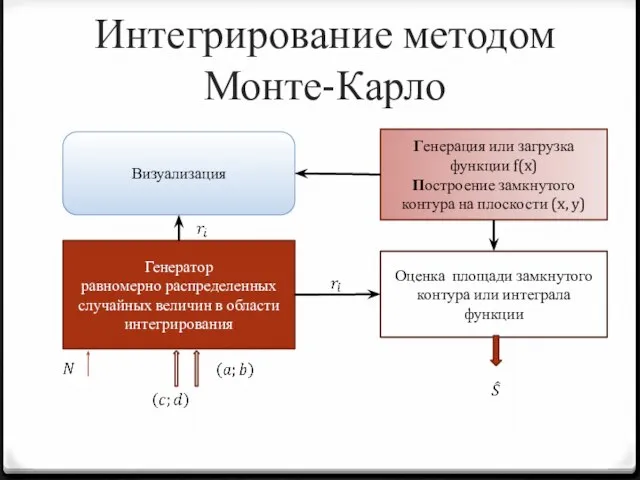
Интегрирование методом Монте-Карло
Генератор
равномерно распределенных случайных величин в области интегрирования
Визуализация
Оценка площади замкнутого контура или интеграла функции
Генерация или загрузка функции f(x)
Построение замкнутого контура на плоскости (x, y)

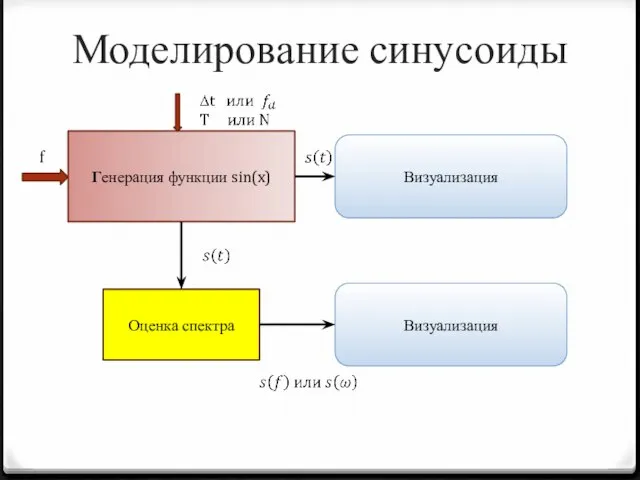
Моделирование синусоиды
Генерация функции sin(x)
Визуализация
Оценка спектра
Визуализация
f

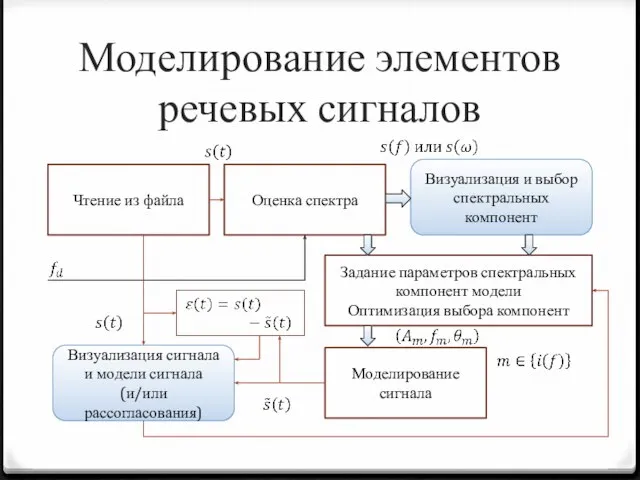
Моделирование элементов речевых сигналов
Чтение из файла
Оценка спектра
Визуализация и выбор спектральных компонент
Задание параметров спектральных компонент модели
Оптимизация выбора компонент
Моделирование сигнала
Визуализация сигнала и модели сигнала (и/или рассогласования)

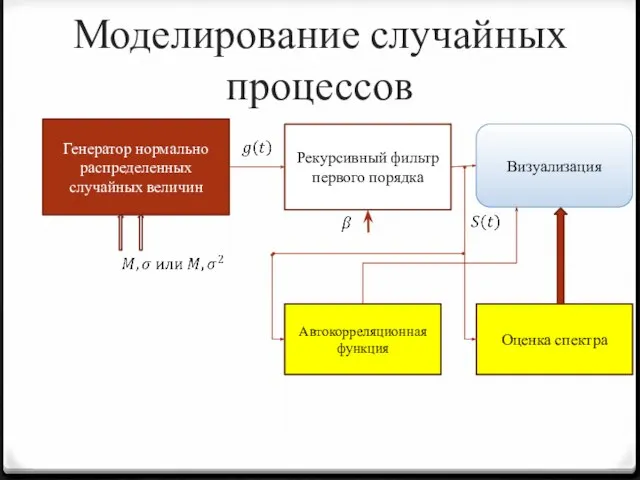
Моделирование случайных процессов
Генератор нормально распределенных случайных величин
Рекурсивный фильтр первого порядка
Визуализация
Оценка спектра
Автокорреляционная функция

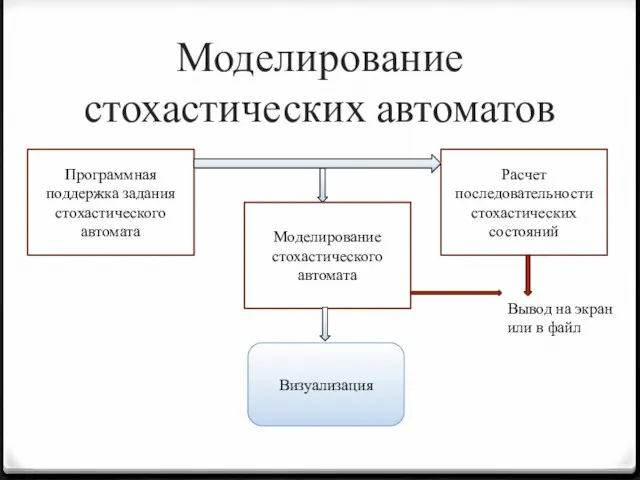
Моделирование стохастических автоматов
Программная поддержка задания стохастического автомата
Моделирование стохастического автомата
Визуализация
Расчет последовательности стохастических состояний
Вывод на экран или в файл

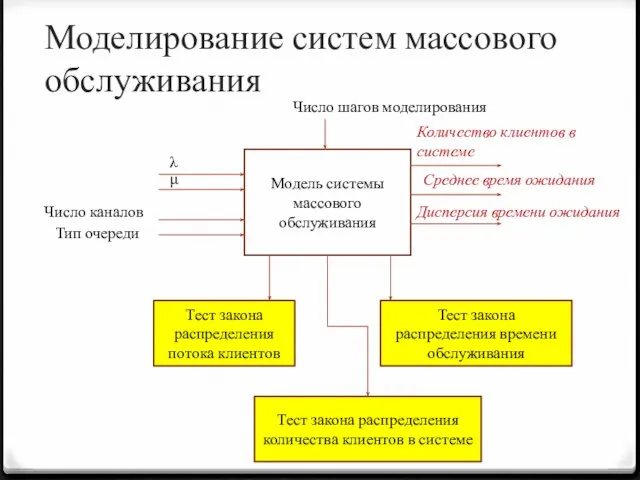
Моделирование систем массового обслуживания
Модель системы массового обслуживания
λ
μ
Тип очереди
Число каналов
Число шагов моделирования
Количество клиентов в системе
Среднее время ожидания
Дисперсия времени ожидания
Тест закона распределения потока клиентов
Тест закона распределения времени обслуживания
Тест закона распределения количества клиентов в системе

Формализованное описание системы массового обслуживания
Элементы системы массового обслуживания:
заявка на обслуживание
механизм обслуживания (обслуживающая система в случае однофазного обслуживания)
Аналитические характеристики
время обслуживания поступившего требования
распределение моментов поступления требований
распределение времени обслуживания требований
Функциональные возможности любой модели массового обслуживания определяются следующими факторами:
распределением моментов поступления заявок на обслуживание (единичных или групповых)
распределением продолжительности обслуживания
конфигурацией обслуживающей системы (последовательное, параллельное или последовательно-параллельное обслуживание)

++
Входные потоки – процессы чистого рождения, выходные – процессы чистой гибели
Режимы – переходной или стационарный
При стационарном режиме анализируют:
вероятность того, что в системе находится n клиентов (заявок на обслуживание)
среднее число находящихся в системе клиентов
среднее число клиентов в очереди
средняя продолжительность пребывания клиента (заявки) в системе
средняя продолжительность пребывания клиента в очереди
Эффективная частота поступлений требований (допущенных в блок ожидания)
дисциплина очереди и приоритетные характеристики
вместимость блока ожидания (ограниченная или неограниченная)
емкость (или мощность) источника требований (конечная или бесконечно большая)
поведенческие характеристики (возможность переходить из одной очереди в другую, отказы от ожидания)

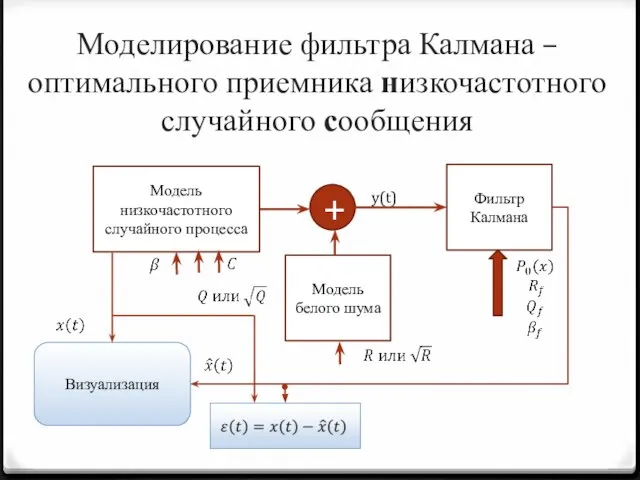
Моделирование фильтра Калмана – оптимального приемника низкочастотного случайного сообщения
Модель низкочастотного случайного процесса
+
y(t)
Модель белого шума
Фильтр Калмана
Визуализация

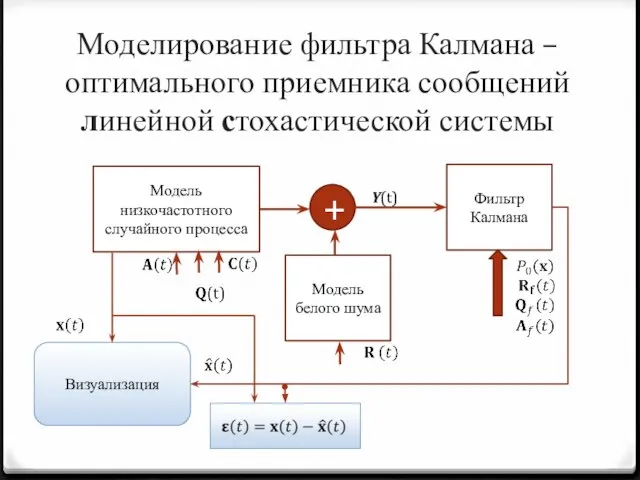
Моделирование фильтра Калмана – оптимального приемника сообщений линейной стохастической системы
Модель низкочастотного случайного процесса
+
Y(t)
Модель белого шума
Фильтр Калмана
Визуализация