Содержание
- 2. § 1.1. Трансляции и трансляторы Определение 1.1. Трансляцией из языка L1 ⊆ Σ* в язык L2
- 3. Хотя в общем случае в трансляции τ одному входному предложению x может соответствовать несколько выходных пред-ложений
- 4. Пример 1.1. Предположим, что мы хотим закодировать некоторый текст с помощью азбуки Морзе. Как известно, в
- 5. Очевидно, что трансляцию предложений, например, на русском языке, в код Морзе можно реализовать с помощью гомомор-физма,
- 6. Для любой входной цепочки x = a1a2 … an, ai∈Σ, i=1,2,…,n, гомоморфизм h позволяет найти соответствующую
- 7. Гомоморфизм h определяет трансляцию τ(h) = {(x, h(x)) | x∈Σ*}. Устройство, которое по заданной цепочке x∈Σ*
- 8. Реалистичным примером транслятора, основанного на гомоморфизме, является простейший ассемблер. Транслятором для данной трансляции τ называется такое
- 9. Желательными свойствами транслятора являются: 1) эффективность (время, затрачиваемое на перевод входной строки, должно быть линейно пропорционально
- 10. § 1.2. Схемы синтаксически управляемой трансляции Трансляторы являются средством реализации трансляций, хотя их можно рассматривать также
- 11. Определение 1.2. Схемой синтаксически управляемой трансляции называется фор-мальная система T = (N, Σ, Δ, R, S),
- 12. A→ α, β, где A∈N, α∈(N∪Σ)*, β∈(N∪Δ)*, причём каждое вхождение нетерминала в цепочку α взаимно однозначно
- 13. Для указания связей между вхожде-ниями нетерминалов можно использовать индексы. Например, связанные вхождения одно-имённых нетерминалов помечаются одина-ковыми
- 14. Определение 1.3. Введем понятие трансляционной формы следующим образом: 1) (S, S) — начальная трансляционная форма, причём
- 15. 2) если (αAβ, α’Aβ’) — трансляционная форма, в которой два явно выделенных вхождения нетерминала A связаны,
- 19. Определение 1.5. Грамматика Gi = (N, Σ, Pi, S), где Pi = {A → α |
- 20. Пример 1.2. Пусть sdts T = ({E, T, F}, {a, +, *, (, )}, {a, +,
- 21. Часть 2: Пример 1.2.
- 22. Нетрудно догадаться, что τ(T) = {(x, y) | x — инфиксная запись, y — эквивалентная постфиксная
- 23. Определение 1.6. Схема синтаксически управляемой трансляции называется простой, если в каждом её правиле A → α,
- 24. Многие, но не все, полезные трансляции могут быть описаны как простые. В примере 1.2 схема T,
- 25. Другими словами, магазинные преобразо-ватели характеризуют класс простых синтаксически управляемых трансляций таким же образом, как магазинные автоматы
- 26. § 1.3. Магазинные преобразователи и синтаксически управляемые трансляции Здесь мы рассмотрим магазинные преобразователи, отличающиеся от мага-зинных
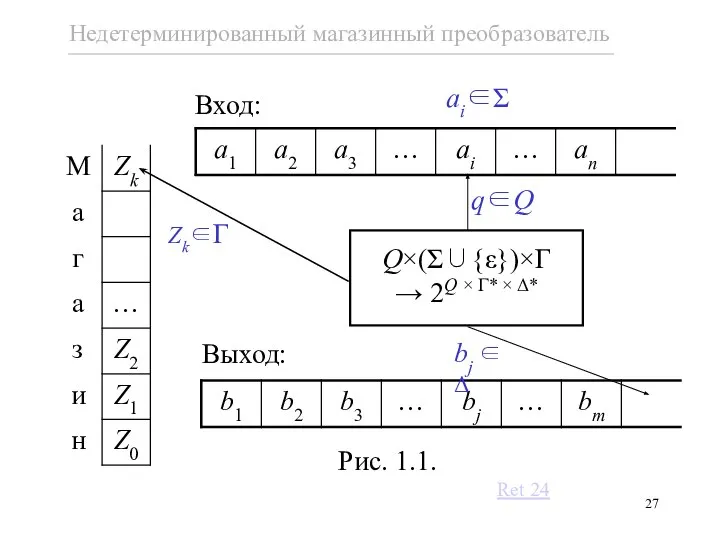
- 27. q∈Q Q×(Σ∪{ε})×Γ → 2Q × Γ* × Δ* Вход: Выход: Рис. 1.1. Ret 24 Zk∈Γ ai∈Σ
- 28. Определение 1.7. Недерминированный магазинный преобразователь (npdt — nondeterministic pushdown transducer) есть формальная система P = (Q,
- 29. Запись δ(q, a, Z) = означает, что npdt P, находясь в состоянии q∈Q, сканируя a∈Σ на
- 30. При этом входная головка сдвигается на одну ячейку вправо, если a ≠ ε, иначе головка остается
- 31. В частности: если a = ε, то выбор действия не зависит от текущего входного символа и,
- 32. В начальный момент q = q0, в магазине находится единственный символ Z0, входная головка сканирует первую
- 33. Определение 1.8. Конфигурацией магазин-ного преобразователя P назовем четверку (q, x, α, y), где q∈Q — текущее
- 34. Таким образом, начальная конфигурация есть (q0,x,Z0,ε), где x обозначает всю входную цепочку. Пусть (q,ax,Zα,y) — текущая
- 35. Как обычно, определяются степень ( ), транзитивное замыкание ( ) и рефлексивно-транзитивное замыкание ( ) этого
- 36. Определение 1.9. Говорят, что y∈Δ* есть выход для x∈Σ* при конечном состоянии, если (q0, x, Z0,
- 37. Говорят, что y∈Δ* есть выход для x∈Σ* при пустом магазине, если (q0, x, Z0, ε) (q,
- 38. Пример 1.3. Пусть pdt P = ({q}, {a, +, *}, {E, +, *}, {a, +, *},
- 40. Определение 1.10. Магазинный преобразова-тель P = (Q, Σ, Γ, Δ, δ, q0, Z0, F) называется детерминированным
- 41. На практике предпочитают использовать детерминированными магазинными преоб-разователями (dpdt), поскольку в реализации они оказываются более эффективными по
- 42. Лемма 1.1. Пусть T = (N, Σ, Δ, R, S) — простая схема синтаксически управляемой трансляции.
- 43. Положим P = ({q}, Σ, N ∪ Σ ∪ Δ’, Δ , δ, q, S, ∅).
- 44. Отображение δ определяется так: 1. (q, x0y0’B1x1y1’…Bmxmym’, ε)∈δ(q,ε,A), если A → x0B1x1 … Bmxm, y0B1y1… Bmym∈R,
- 45. Ret 52
- 48. На первом шаге данного вывода было применено правило A → x0B1x1B2x2…Bmxm, y0B1y1B2y2…Bmym∈R и потому согласно п.1
- 49. Рассмотрим движения pdt P. Учитывая условия (1.1) и (1.3), имеем (q, x, A, ε) = (q,
- 55. Кроме того, магазинная цепочка, заме-щающая A на вершине магазина, должна начинаться на x, так как только
- 58. Поскольку в исходной конфигурации на вершине магазина A∈N, то первое же движение — типа 1: (q,
- 61. Далее мы можем повторить рассуждения, аналогичные предыдущим, относя их к цепочкам xi∈Σ*, yi’∈Δ’ (i = 1,
- 64. В частности, при A = S следует утверж-дение II. Из рассуждений I и II следует утверждение
- 65. Пример 1.4. Пусть sdts T = ({E}, {a, +, *}, {a, +, *}, R, E), где
- 67. Лемма 1.2. Пусть P = (Q, Σ, Γ, Δ, δ, q0, Z0, ∅) — недетерминированный магазинный
- 76. Из (1.15) следует, что существует правило [qZp] → a[q1Z1q2]…[qmZmqm+1], y[q1Z1q2]…[qmZmqm+1]∈R, которое обязано своим происхождение тому, что
- 80. Из лемм 1.1 и 1.2 следует Теорема 1.1. Трансляция τ = τ(T), где T — простая
- 81. Пример 1.5. В предыдущем примере по простой sdts T = ({E},{a, +, *}, {a, +, *},
- 82. Теперь по этому недетерминированному преобразователю P мы построим эквива-лентную простую схему синтаксически управляемой трансляции, воспользовав-шись алгоритмом,
- 83. Положим T = ({S, [qEq], [qaq], [q+q], [q*q], [qa’q], [q+’q], [q*’q]}, {a, +, *},{a, +, *},
- 84. Эта схема мало похожа на исходную, в которой было всего три правила. Однако её можно эквивалентными
- 86. Скачать презентацию
















































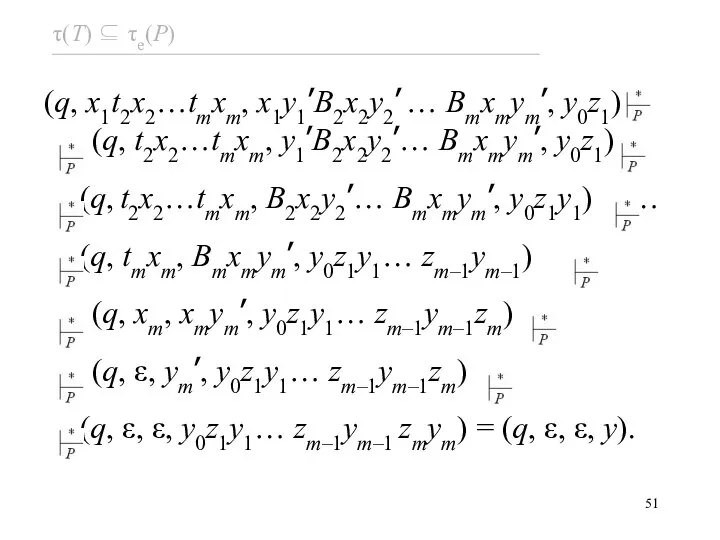
























![Из (1.15) следует, что существует правило [qZp] → a[q1Z1q2]…[qmZmqm+1], y[q1Z1q2]…[qmZmqm+1]∈R, которое обязано](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1159072/slide-75.jpg)






![Положим T = ({S, [qEq], [qaq], [q+q], [q*q], [qa’q], [q+’q], [q*’q]}, {a,](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1159072/slide-82.jpg)

 Алгоритмы. Алгоритм Эратросфена. Виды алгоритмов
Алгоритмы. Алгоритм Эратросфена. Виды алгоритмов Лямбда-архитектура
Лямбда-архитектура Деревья решений
Деревья решений Информационные модели: системы и структуры данных
Информационные модели: системы и структуры данных Инструменты графического редактора Paint
Инструменты графического редактора Paint Устранение цифрового неравенства в Матвеевском районе
Устранение цифрового неравенства в Матвеевском районе Особенности современных ЭВМ
Особенности современных ЭВМ Pascal ABC. Работа с числовыми данными. Целые числа. Урок 3-4
Pascal ABC. Работа с числовыми данными. Целые числа. Урок 3-4 Электронное портфолио школьника. Участвуй-заполняй-побеждай
Электронное портфолио школьника. Участвуй-заполняй-побеждай Университетская газета Молодость
Университетская газета Молодость Словесные информационные модели
Словесные информационные модели Адресация в интернете
Адресация в интернете Мобильные приложения как средство изучения иностранного языка
Мобильные приложения как средство изучения иностранного языка MSE block library for Simulink
MSE block library for Simulink DIDO Wi Fi (Distributed Input Distributed Output)
DIDO Wi Fi (Distributed Input Distributed Output) Искусственный интеллект
Искусственный интеллект Работа с таблицами (10 класс)
Работа с таблицами (10 класс) Множества
Множества Обзор интернет-ресурсов, программ и приложений по созданию интерактивных пособий, презентаций и дидактических игр
Обзор интернет-ресурсов, программ и приложений по созданию интерактивных пособий, презентаций и дидактических игр Технологии и опыт мирового уровня в области системной интеграции и разработки программного обеспечения
Технологии и опыт мирового уровня в области системной интеграции и разработки программного обеспечения Получение сведений из фонда данных государственной кадастровой оценки
Получение сведений из фонда данных государственной кадастровой оценки Электронная система расписания
Электронная система расписания Практика в газете Пермский университет
Практика в газете Пермский университет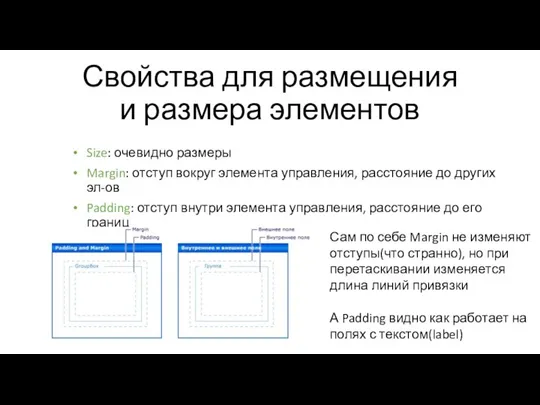 Свойства для размещения и размера элементов
Свойства для размещения и размера элементов Мобильная служба организации краткосрочных событий
Мобильная служба организации краткосрочных событий Школа программирования
Школа программирования Знакомство с новой лексикой
Знакомство с новой лексикой Рекламный интернет-проект ШУМ
Рекламный интернет-проект ШУМ