Содержание
- 2. Цифровая сортировка (DigitalSort) Вначале числа из списка S распределяются по очередям, причём номер очереди определяется последней
- 3. В общем случае: Дана последовательность из S чисел, представленных в m-ичной системе счисления. Каждое число состоит
- 4. Пример. Необходимо сортировать последовательность целых чисел типа longint (32 бита). Сколько потребуется очередей? Можно рассматривать каждый
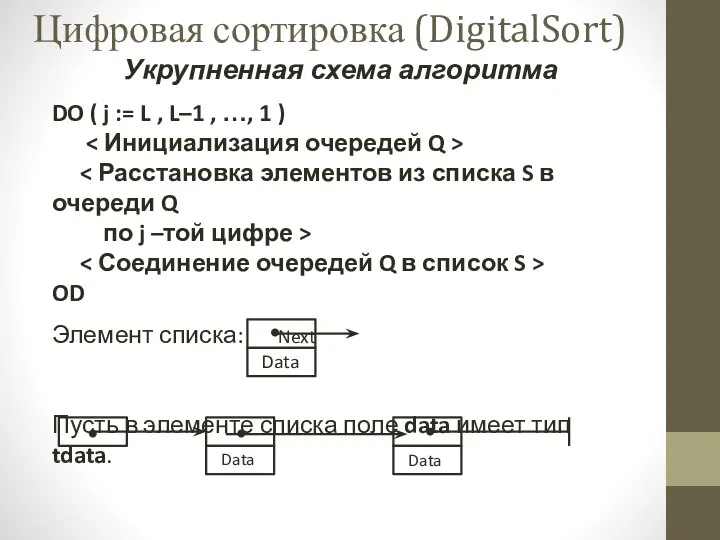
- 5. Укрупненная схема алгоритма DO ( j := L , L–1 , …, 1 ) по j
- 6. Рассмотрим основные операции: 1) Определение j-той цифры ключа сортировки Задача: выделение произвольного байта в поле Data
- 7. Рассмотрим особенности реализации цифровой сортировки для сложных структур: Пример: struct tData { char Name [5]; long
- 8. sizeof (tData) = 10 байтов старш. млад. млад. старш. name phone Используем индексацию для удобства выбора
- 9. Тогда KDI [j] - номер байта, соответствующего j-той цифре ключа сортировки, j := L, L–1, …,1.
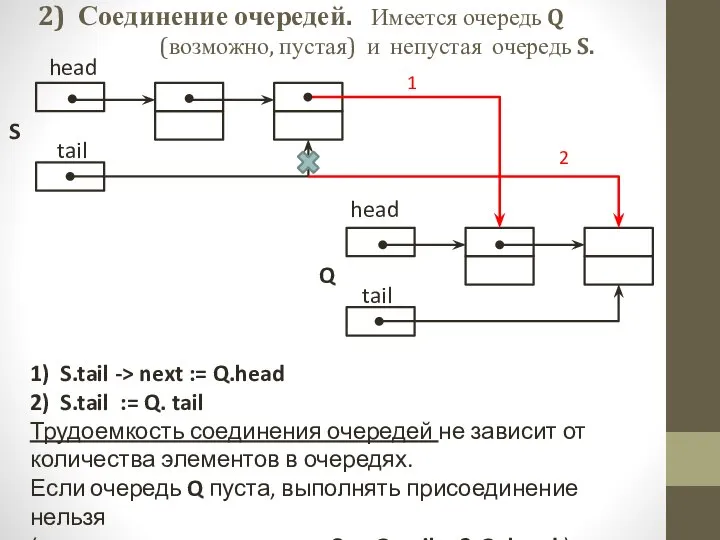
- 10. 2) Соединение очередей. Имеется очередь Q (возможно, пустая) и непустая очередь S. 1) S.tail -> next
- 11. Алгоритм на псевдокоде DO ( j := L, L-1, … 1 ) DO ( i :=
- 12. Алгоритм на псевдокоде (продолжение) p := & S DO ( i := 0, 1, … 255
- 13. Трудоемкость метода T = O( L( n + m ) ) Замечания: 1) Цифровая сортировка устойчива.
- 15. Скачать презентацию






![Тогда KDI [j] - номер байта, соответствующего j-той цифре ключа сортировки, j](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/953894/slide-8.jpg)



 Построение таблиц истинности
Построение таблиц истинности Регистрация ЮЛ на Портале НБ
Регистрация ЮЛ на Портале НБ Программирование и алгоритмизация. Основы программирования. Лекция 4
Программирование и алгоритмизация. Основы программирования. Лекция 4 Знакомство с 3D-технологиями
Знакомство с 3D-технологиями Касса
Касса Большая перемена. Регистрация
Большая перемена. Регистрация Установка RSA SecurID
Установка RSA SecurID Защита информации от утечки на объектах информатизации органов внутренних дел
Защита информации от утечки на объектах информатизации органов внутренних дел Программирование (АлгЯзык)
Программирование (АлгЯзык)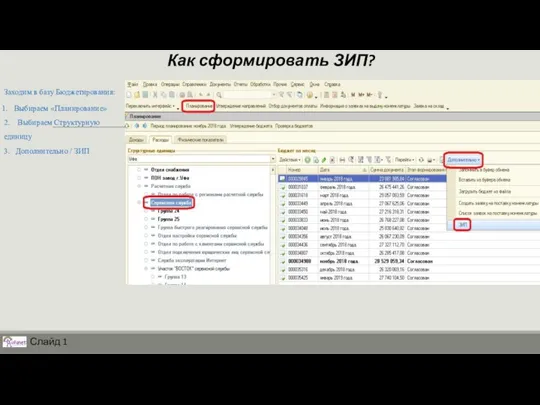 Как сформировать ЗИП?
Как сформировать ЗИП? Способы записи алгоритмов
Способы записи алгоритмов Презентация "Виды моделей данных" - скачать презентации по Информатике
Презентация "Виды моделей данных" - скачать презентации по Информатике Локальная сеть
Локальная сеть Медицинская информационная система ТрастМед: единая платформа информатизации
Медицинская информационная система ТрастМед: единая платформа информатизации ВКР: Применение методов оптимизации для формирования обобщенных кодов Баркера
ВКР: Применение методов оптимизации для формирования обобщенных кодов Баркера Сетевая безопасность. Основные понятия. Типы и примеры атак
Сетевая безопасность. Основные понятия. Типы и примеры атак Введение в платформу .Net
Введение в платформу .Net Вложенные циклы
Вложенные циклы УЦ УГМК-Холдинг
УЦ УГМК-Холдинг Функции вывода сообщений
Функции вывода сообщений Google. Топ фактів
Google. Топ фактів Библиотека на колёсах
Библиотека на колёсах Достижения белорусских ученых
Достижения белорусских ученых Передача информации
Передача информации Сервисы интернет
Сервисы интернет 2._Работа_с_файловой_системой
2._Работа_с_файловой_системой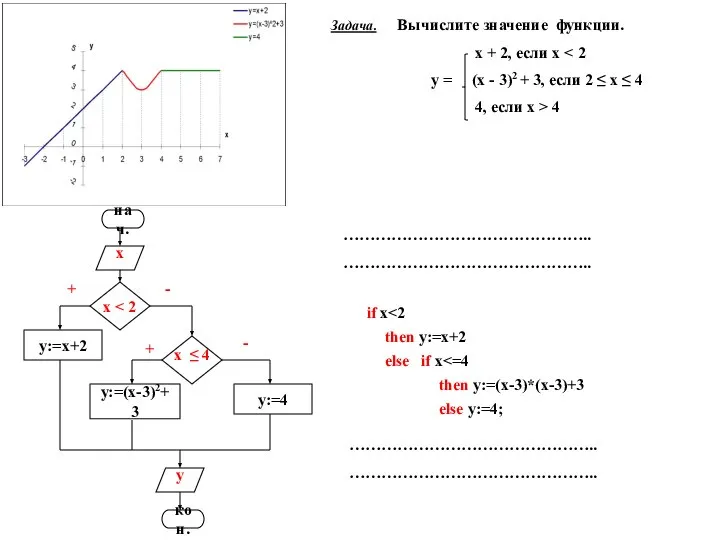 Вложенные ветвления
Вложенные ветвления Введение Лекция 1
Введение Лекция 1