ВКР: Математическое и программное обеспечение для исследования простых эвристик при решении задач линейного раскроя
Содержание
- 2. Цель работы: Сравнение эффективности различных алгоритмов для решения разных классов задач линейного раскроя на основе вычислительного
- 3. ПОСТАНОВКА ЗАДАЧИ
- 4. СТРУКТУРА РЕШЕНИЯ
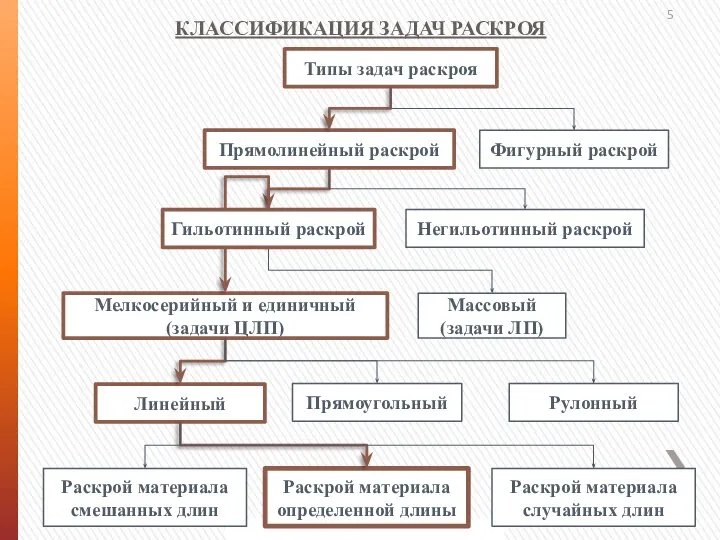
- 5. КЛАССИФИКАЦИЯ ЗАДАЧ РАСКРОЯ
- 6. ЗАДАЧА ЛИНЕЙНОГО РАСКРОЯ В УСЛОВИЯХ ЕДИНИЧНОГО (МЕЛКОСЕРИЙНОГО) ПРОИЗВОДСТВА ПОСТАНОВКА ЗАДАЧИ МАТЕМАТИЧЕСКАЯ МОДЕЛЬ
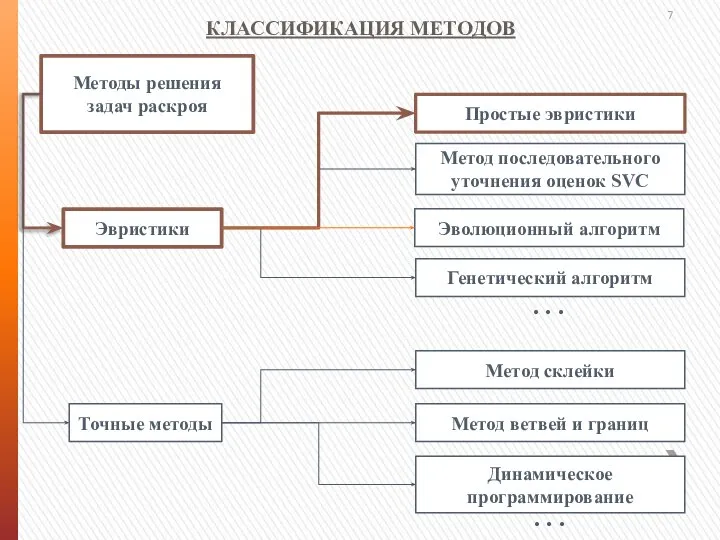
- 7. КЛАССИФИКАЦИЯ МЕТОДОВ . . . . . .
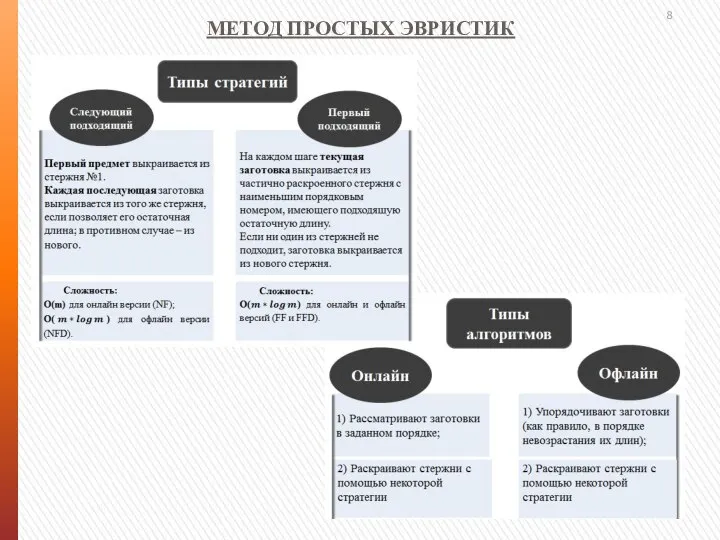
- 8. МЕТОД ПРОСТЫХ ЭВРИСТИК
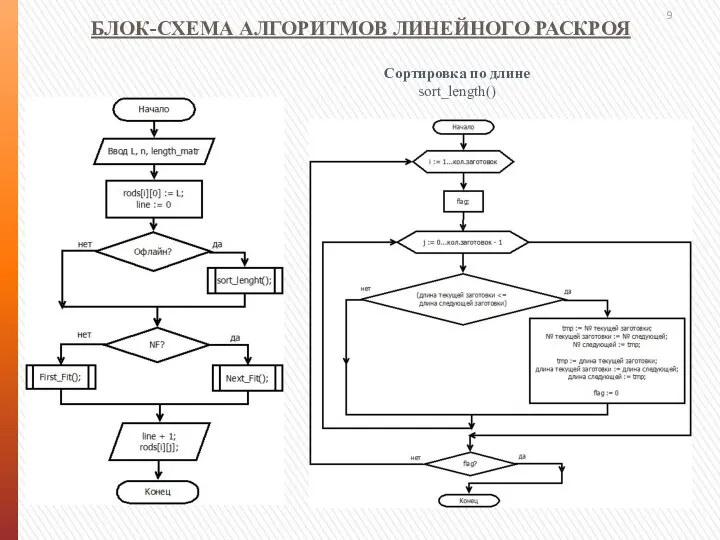
- 9. БЛОК-СХЕМА АЛГОРИТМОВ ЛИНЕЙНОГО РАСКРОЯ Сортировка по длине sort_length()
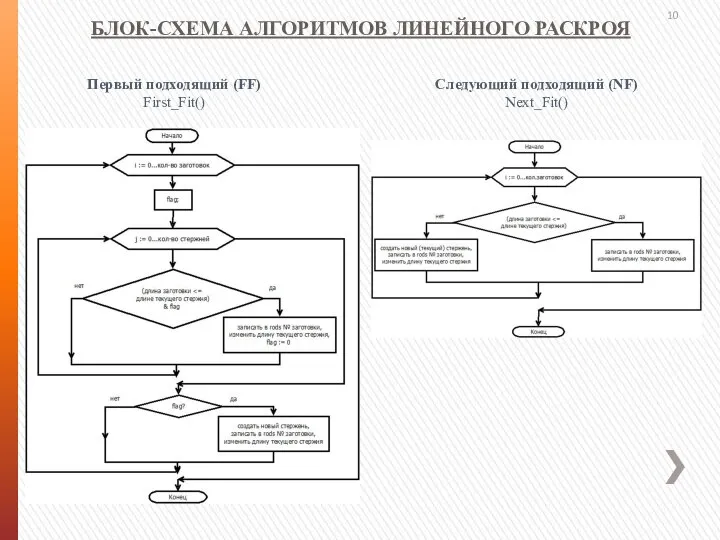
- 10. БЛОК-СХЕМА АЛГОРИТМОВ ЛИНЕЙНОГО РАСКРОЯ Следующий подходящий (NF) Next_Fit() Первый подходящий (FF) First_Fit()
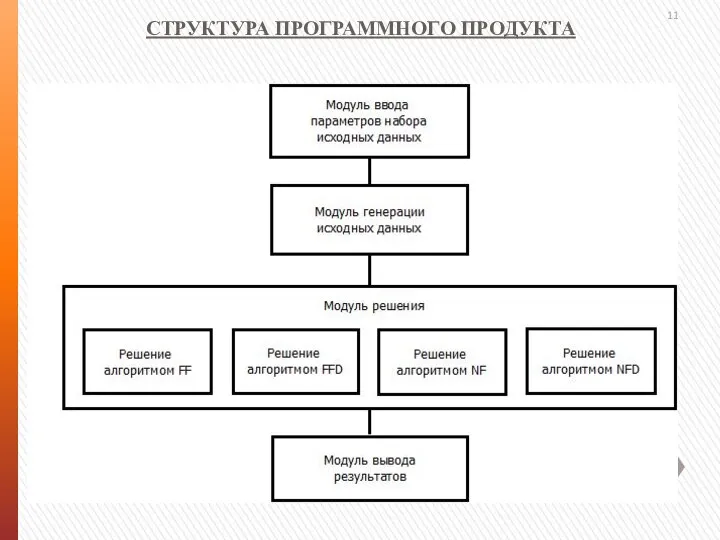
- 11. СТРУКТУРА ПРОГРАММНОГО ПРОДУКТА
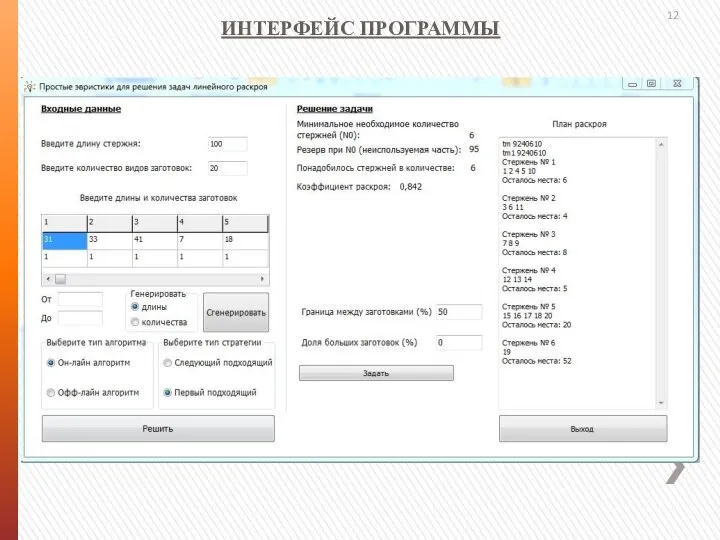
- 12. ИНТЕРФЕЙС ПРОГРАММЫ
- 13. установить параметры исходных данных (границу между большими и маленькими заготовками, долю больших заготовок в общем количестве
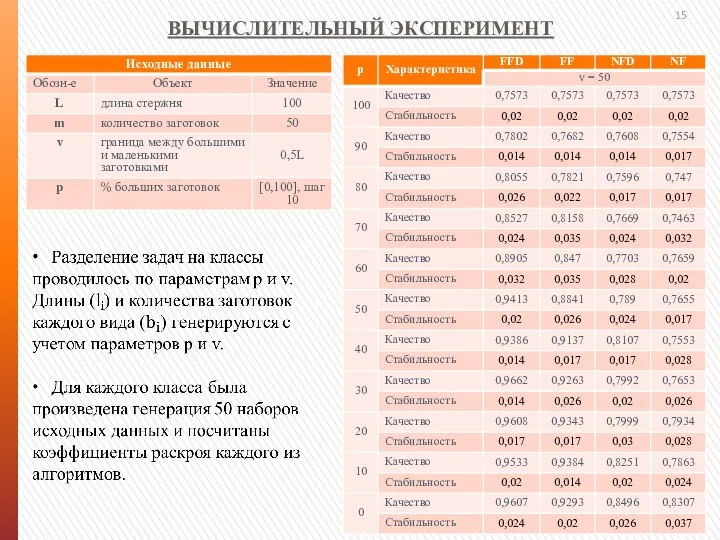
- 14. ВЫЧИСЛИТЕЛЬНЫЙ ЭКСПЕРИМЕНТ
- 15. ВЫЧИСЛИТЕЛЬНЫЙ ЭКСПЕРИМЕНТ
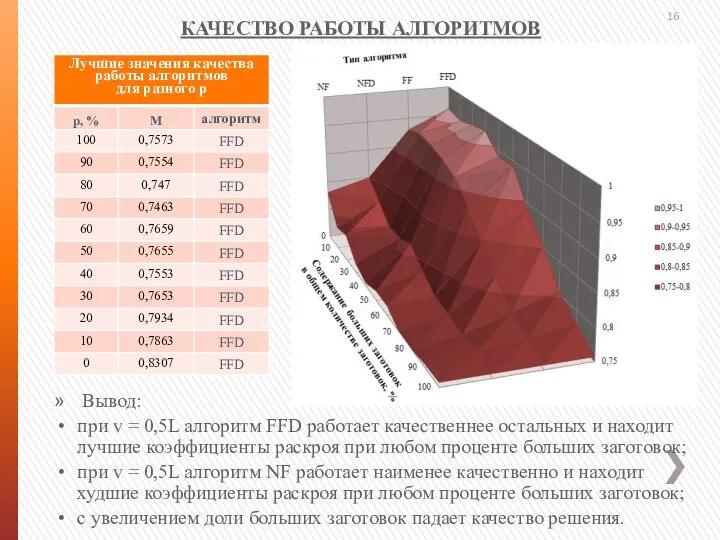
- 16. Вывод: при v = 0,5L алгоритм FFD работает качественнее остальных и находит лучшие коэффициенты раскроя при
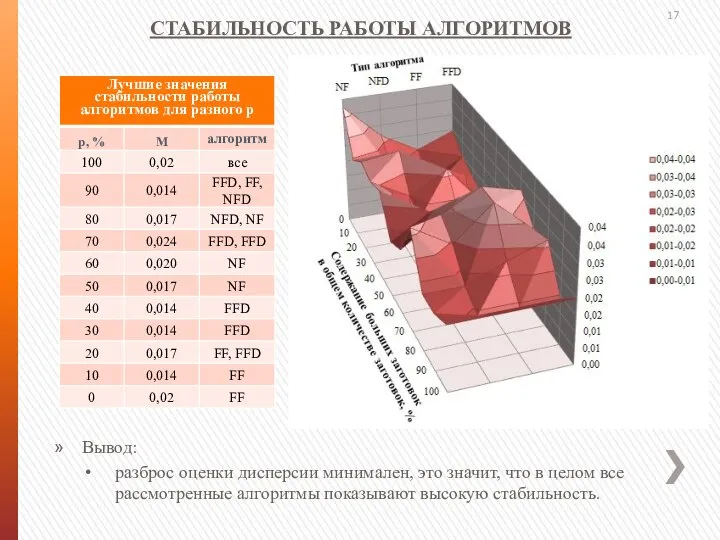
- 17. Вывод: разброс оценки дисперсии минимален, это значит, что в целом все рассмотренные алгоритмы показывают высокую стабильность.
- 18. РЕЗУЛЬТАТЫ ВКР выполнен аналитический обзор методов решения целочисленных задач линейного раскроя и выбран для реализации метод
- 20. Скачать презентацию







 Работа с файлами С++/ Многопоточность
Работа с файлами С++/ Многопоточность Примеры библиографических записей
Примеры библиографических записей Разработка информационных систем
Разработка информационных систем Графическое оформление соцсетей
Графическое оформление соцсетей Организация дистанционного обучения с использованием системы Skype
Организация дистанционного обучения с использованием системы Skype Алгоритмизация вычислений
Алгоритмизация вычислений Интерфейсы: interface IMy
Интерфейсы: interface IMy Динамический web-сайт. Программные модули и элементы динамического контента
Динамический web-сайт. Программные модули и элементы динамического контента Работа с лайт микшером
Работа с лайт микшером Клиент-серверная web-система для распространения билетов в театр
Клиент-серверная web-система для распространения билетов в театр Работа с ПК. Тема 1 занятие 2
Работа с ПК. Тема 1 занятие 2 Implementation of std::common_type
Implementation of std::common_type Использование Api во всемирной паутине
Использование Api во всемирной паутине Technology and digital devices might not replace traditional, paper bedtime books. (5)
Technology and digital devices might not replace traditional, paper bedtime books. (5) Сюжет и дополнения. Стражи
Сюжет и дополнения. Стражи Корпоративный портал iDesk
Корпоративный портал iDesk Книжная графика, как активный медиасигнал. Раскрытие специфики детской книжной иллюстрации
Книжная графика, как активный медиасигнал. Раскрытие специфики детской книжной иллюстрации Всероссийская акция Час кода
Всероссийская акция Час кода Массивы. Класс Array
Массивы. Класс Array Ключевые слова
Ключевые слова Проект локальной компьютерной сети для охранного агентства с разработкой системы видеонаблюдения
Проект локальной компьютерной сети для охранного агентства с разработкой системы видеонаблюдения тестирование смэв 2022
тестирование смэв 2022 Drive Ahead Valentine’s Day Event
Drive Ahead Valentine’s Day Event Построение простой сети
Построение простой сети МИФы нашей школы
МИФы нашей школы информатика Художиткова
информатика Художиткова Superheroes in villais
Superheroes in villais Система управления базами данных моделирование и формализация
Система управления базами данных моделирование и формализация