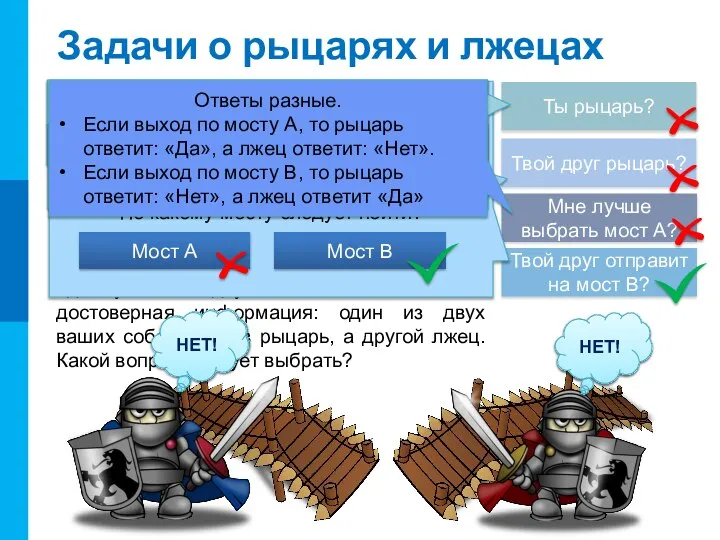
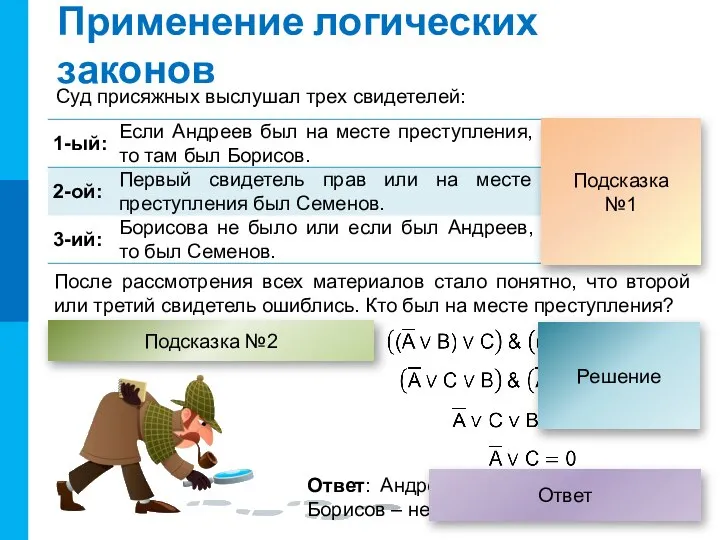
рыцари и лжецы. Покинуть остров можно по одному из двух мостов (А или B). Один из мостов приведет вас на большую землю и вы спасены. Другой мост ведет на непроходимые болота. Для того, чтобы выбраться, у вас есть возможность обратиться с единственным вопросом к одному из двух жителей. Имеется достоверная информация: один из двух ваших собеседников рыцарь, а другой лжец. Какой вопрос следует выбрать?
Твой друг отправит на мост В?
Ты рыцарь?
Твой друг рыцарь?
Мне лучше выбрать мост А?
Ответы одинаковые.
Рыцарь говорит правду про ответ лжеца, а лжец врет про ответ рыцаря.
По какому мосту следует пойти?
Оба отвечают одинаково.
Но информации о выходе нет.
Оба отвечают одинаково.
Но информации о выходе нет.
Ответы разные.
Если выход по мосту А, то рыцарь ответит: «Да», а лжец ответит: «Нет».
Если выход по мосту B, то рыцарь ответит: «Нет», а лжец ответит «Да»
ДА!!!
ДА!!!
НЕТ!
НЕТ!
Мост A
Мост В



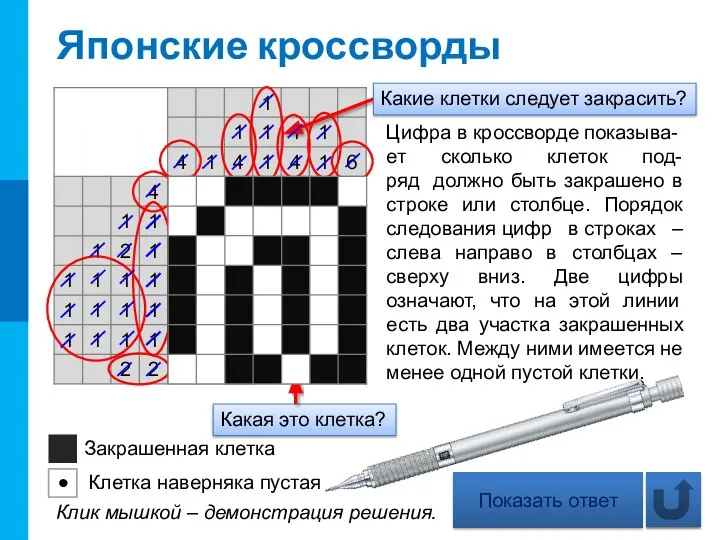

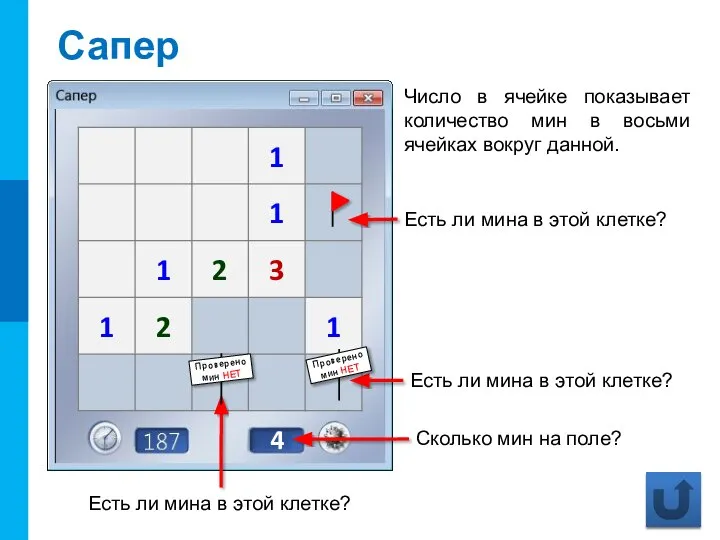



 Базовые типы и операторы языка C#
Базовые типы и операторы языка C# Медиа и массовая культура
Медиа и массовая культура Программирование. Базовая архитектура IBM PC Х86
Программирование. Базовая архитектура IBM PC Х86 Компьютерный вирусы
Компьютерный вирусы Алгоритмы в нашей жизни
Алгоритмы в нашей жизни Устройство компьютера. 2 класс
Устройство компьютера. 2 класс Инструкция по настройке UMB
Инструкция по настройке UMB Язык программирования паскаль. Начала программирования
Язык программирования паскаль. Начала программирования Системы счисления. Математические основы информатики
Системы счисления. Математические основы информатики Топология сетей. Тест
Топология сетей. Тест Разборы задач №3 - бинарный поиск и перебор
Разборы задач №3 - бинарный поиск и перебор Защита информации. Лекция 12
Защита информации. Лекция 12 Программирование и языки программирования
Программирование и языки программирования Палитры цветов в системах цветопередачи RGB, CMYK и HSB
Палитры цветов в системах цветопередачи RGB, CMYK и HSB Презентация на тему Информация
Презентация на тему Информация  Система распознавания лиц для контроля доступа на объект
Система распознавания лиц для контроля доступа на объект Понятие программное обеспечение
Понятие программное обеспечение Угрозы безопасности и методы защиты информации в общественных организациях
Угрозы безопасности и методы защиты информации в общественных организациях Состав вычислительной системы (лекция 1)
Состав вычислительной системы (лекция 1) Практическая схема реализации метода покоординатного спуска с поиском по образцу
Практическая схема реализации метода покоординатного спуска с поиском по образцу Презентация на тему Операторы линейных программ
Презентация на тему Операторы линейных программ  День защиты информации
День защиты информации Киберспорт
Киберспорт Ваша видеоконференцсвязь
Ваша видеоконференцсвязь Представление об организации баз данных и системах управления базами данных
Представление об организации баз данных и системах управления базами данных Библиотечные функции. Синтаксис использования функции в программе: the_root = sqrt(9.0)
Библиотечные функции. Синтаксис использования функции в программе: the_root = sqrt(9.0) Поисковые каналы изменили журналистику. Видео и трансляции, визуальная журналистика
Поисковые каналы изменили журналистику. Видео и трансляции, визуальная журналистика Локаальные сети. Лекция 1
Локаальные сети. Лекция 1