Вычисления по формулам с использованием встроенных математических функций MS EXCEL

Основные понятия
Формула задает правило для вычисления нового значения через исходные значения.Она должна подчиняться определенным правилам записи,т.е. cинтаксису.
Формулой в MS Excel называется последовательность,содержащая следующие элементы:
Знак равенства(=);
Операнды (числа,текст,ссылки на ячейки,ссылки на массивы ячеек,встроенные функции);
Знаки операций (иногда их называют операторами);
Круглые скобки,причем число открывающихся скобок должно быть равно числу закрывающих.

Математические функции

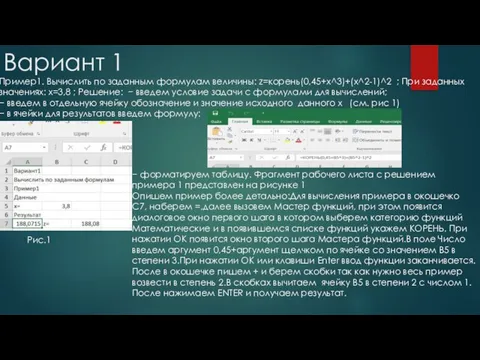
Вариант 1
Рис.1
Пример1. Вычислить по заданным формулам величины: z=корень(0,45+x^3)+(x^2-1)^2 ; При заданных значениях: x=3,8 ; Решение: − введем условие задачи с формулами для вычислений; − введем в отдельную ячейку обозначение и значение исходного данного x (см. рис 1) − в ячейки для результатов введем формулу:
− форматируем таблицу. Фрагмент рабочего листа с решением примера 1 представлен на рисунке 1
Опишем пример более детально:Для вычисления примера в окошечко C7, наберем =,далее вызовем Мастер функций, при этом появится диалоговое окно первого шага в котором выберем категорию функций Математические и в появившемся списке функций укажем КОРЕНЬ. При нажатии OK появится окно второго шага Мастера функций.В поле Число введем аргумент 0,45+аргумент щелчком по ячейке со значением B5 в степени 3.При нажатии OK или клавиши Enter ввод функции заканчивается.После в окошечке пишем + и берем скобки так как нужно весь пример возвести в степень 2.В скобках вычитаем ячейку B5 в степени 2 с числом 1.После нажимаем ENTER и получаем результат.

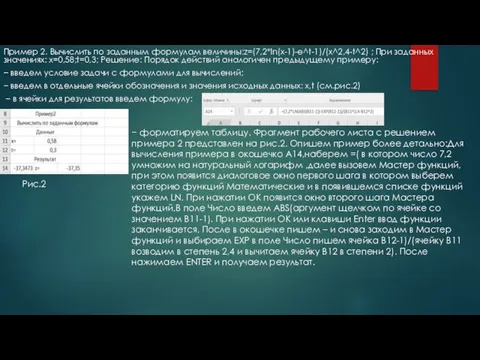
Пример 2. Вычислить по заданным формулам величины:z=(7,2*ln(x-1)-e^t-1)/(x^2,4-t^2) ; При заданных значениях: x=0,58;t=0,3; Решение: Порядок действий аналогичен предыдущему примеру:
− введем условие задачи с формулами для вычислений;
− введем в отдельные ячейки обозначения и значения исходных данных: x,t (см.рис.2)
− в ячейки для результатов введем формулу:
Рис.2
− форматируем таблицу. Фрагмент рабочего листа с решением примера 2 представлен на рис.2. Опишем пример более детально:Для вычисления примера в окошечко A14,наберем =( в котором число 7,2 умножим на натуральный логарифм ,далее вызовем Мастер функций, при этом появится диалоговое окно первого шага в котором выберем категорию функций Математические и в появившемся списке функций укажем LN. При нажатии OK появится окно второго шага Мастера функций.В поле Число введем ABS(аргумент щелчком по ячейке со значением B11-1). При нажатии OK или клавиши Enter ввод функции заканчивается. После в окошечке пишем – и снова заходим в Мастер функций и выбираем EXP в поле Число пишем ячейка B12-1)/(ячейку B11 возводим в степень 2,4 и вычитаем ячейку B12 в степени 2). После нажимаем ENTER и получаем результат.

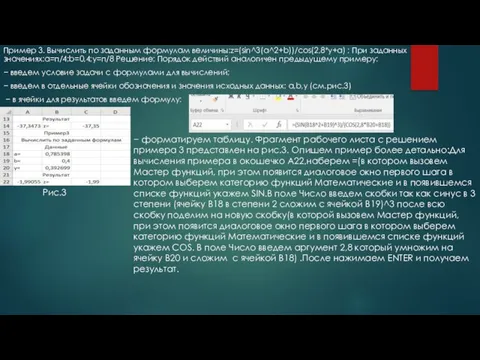
Пример 3. Вычислить по заданным формулам величины:z=(sin^3(a^2+b))/cos(2,8*y+a) ; При заданных значениях:a=п/4;b=0,4;y=п/8 Решение: Порядок действий аналогичен предыдущему примеру:
− введем условие задачи с формулами для вычислений;
− введем в отдельные ячейки обозначения и значения исходных данных: a,b,y (см.рис.3)
− в ячейки для результатов введем формулу:
Рис.3
− форматируем таблицу. Фрагмент рабочего листа с решением примера 3 представлен на рис.3. Опишем пример более детально:Для вычисления примера в окошечко A22,наберем =(в котором вызовем Мастер функций, при этом появится диалоговое окно первого шага в котором выберем категорию функций Математические и в появившемся списке функций укажем SIN.В поле Число введем скобки так как синус в 3 степени (ячейку B18 в степени 2 сложим с ячейкой B19)^3 после всю скобку поделим на новую скобку(в которой вызовем Мастер функций, при этом появится диалоговое окно первого шага в котором выберем категорию функций Математические и в появившемся списке функций укажем COS. В поле Число введем аргумент 2,8 который умножим на ячейку B20 и сложим с ячейкой B18) .После нажимаем ENTER и получаем результат.

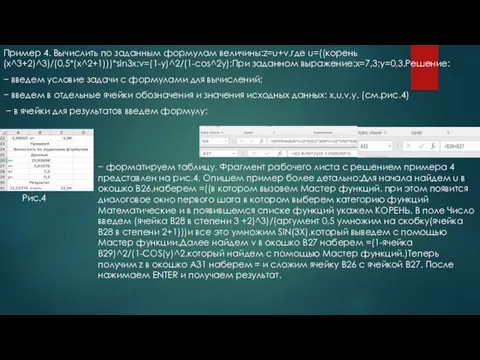
Пример 4. Вычислить по заданным формулам величины:z=u+v,где u=((корень(x^3+2)^3)/(0,5*(x^2+1)))*sin3x;v=(1-y)^2/(1-cos^2y);При заданном выражение:x=7,3;y=0,3.Решение:
− введем условие задачи с формулами для вычислений;
− введем в отдельные ячейки обозначения и значения исходных данных: x,u,v,y. (см.рис.4)
− в ячейки для результатов введем формулу:
Рис.4
− форматируем таблицу. Фрагмент рабочего листа с решением примера 4 представлен на рис.4. Опишем пример более детально:Для начала найдем u в окошко B26,наберем =((в котором вызовем Мастер функций, при этом появится диалоговое окно первого шага в котором выберем категорию функций Математические и в появившемся списке функций укажем КОРЕНЬ. В поле Число введем (ячейка B28 в степени 3 +2)^3)/(аргумент 0,5 умножим на скобку(ячейка B28 в степени 2+1)))и все это умножим SIN(3X),который выведем с помощью Мастер функции.Далее найдем v в окошко B27 наберем =(1-ячейка B29)^2/(1-COS(y)^2,который найдем с помощью Мастер функций.)Теперь получим z в окошко A31 наберем = и сложим ячейку B26 с ячейкой B27. После нажимаем ENTER и получаем результат.

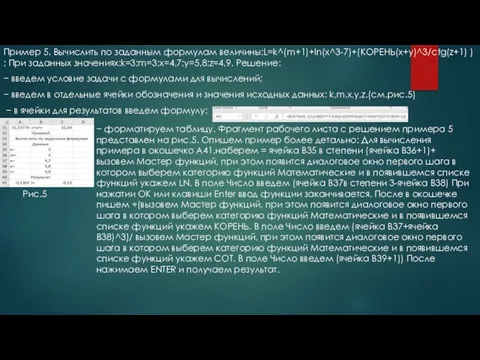
Пример 5. Вычислить по заданным формулам величины:L=k^(m+1)+ln(x^3-7)+(КОРЕНЬ(x+y)^3/ctg(z+1) ) ; При заданных значениях:k=3;m=3;x=4,7;y=5,8;z=4,9. Решение:
− введем условие задачи с формулами для вычислений;
− введем в отдельные ячейки обозначения и значения исходных данных: k,m,x,y,z.(см.рис.5)
− в ячейки для результатов введем формулу:
Рис.5
− форматируем таблицу. Фрагмент рабочего листа с решением примера 5 представлен на рис.5. Опишем пример более детально: Для вычисления примера в окошечко A41,наберем = ячейка B35 в степени (ячейка B36+1)+ вызовем Мастер функций, при этом появится диалоговое окно первого шага в котором выберем категорию функций Математические и в появившемся списке функций укажем LN. В поле Число введем (ячейка B37в степени 3-ячейка B38) При нажатии OK или клавиши Enter ввод функции заканчивается. После в окошечке пишем +(вызовем Мастер функций, при этом появится диалоговое окно первого шага в котором выберем категорию функций Математические и в появившемся списке функций укажем КОРЕНЬ. В поле Число введем (ячейка B37+ячейка B38)^3)/ вызовем Мастер функций, при этом появится диалоговое окно первого шага в котором выберем категорию функций Математические и в появившемся списке функций укажем COT. В поле Число введем (ячейка B39+1)) После нажимаем ENTER и получаем результат.

Вывод:
Я ВЫЧИСЛИЛ ВСЕ ПРИМЕРЫ С ИСПОЛЬЗОВАНИЕМ ВСТРОЕННЫХ МАТЕМАТИЧЕСКИЙ ФУНКЦИЙ MS EXCEL

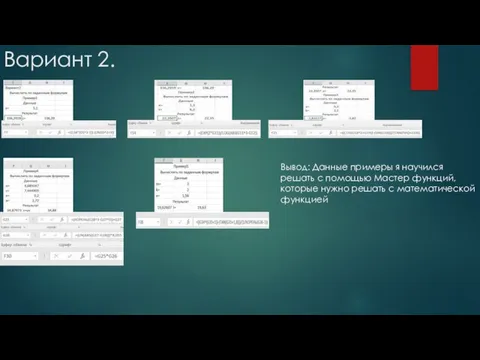
Вариант 2.
Вывод: Данные примеры я научился решать с помощью Мастер функций,которые нужно решать с математической функцией

Вариант 3.
Вывод:Для расчета этих примеров я воспользовался встроенными математическими функциями.

Вариант 4.
Вывод:в данном варианте я смог посчитать большие примеры благодаря математической функции.

Вариант 5.
Вывод: Данные примеры я решил с помощью Мастер функций,которые нужно решать с математической функцией

Вариант 6.
Вывод:Для расчета этих примеров я воспользовался встроенными математическими функциями.

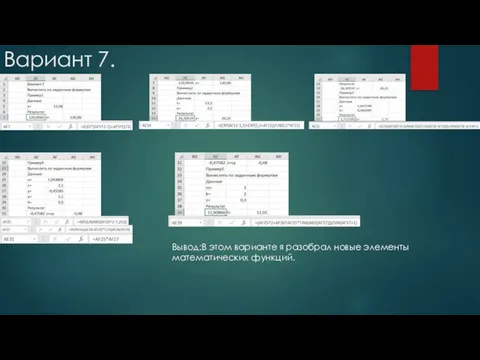
Вариант 7.
Вывод:В этом варианте я разобрал новые элементы математических функций.

Вариант 8.
Вывод:в данном варианте я смог посчитать большие примеры благодаря математической функции.

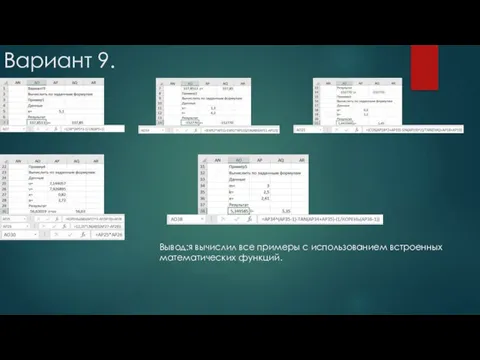
Вариант 9.
Вывод:я вычислил все примеры с использованием встроенных математических функций.

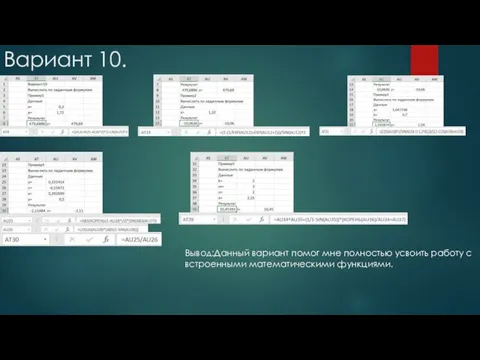
Вариант 10.
Вывод:Данный вариант помог мне полностью усвоить работу с встроенными математическими функциями.

Ссылка на Excel файл с решенными задачами
Excel.xlsx