Слайд 2Симплекс-метод
Данный метод является методом целенаправленного перебора опорных решений задачи линейного программирования. Он

позволяет за конечное число шагов либо найти оптимальное решение, либо установить, что оптимальное решение отсутствует.
Слайд 3Историческая справка
В работе Л. В. Канторовича «Математические методы организации и планирования производства»

(1939) были впервые изложены принципы новой отрасли математики, которая позднее получила название линейного программирования.
Исторически общая задача линейного программирования была впервые поставлена в 1947 году Джорджем Бернардом Данцигом, Маршаллом Вудом и их сотрудниками в департаменте военно-воздушных сил США. В то время эта группа занималась исследованием возможности использования математических и смежных с ними методов для военных задач и проблем планирования. В дальнейшем для развития этих идей в ВВС была организована исследовательская группа под названием Project SCOOP. Первое успешное решение задачи линейного программирования на ЭВМ SEAC было проведено в январе 1952 года.
Слайд 4Основное содержание симплексного метода заключается в следующем:
Указать способ нахождения оптимального опорного решения;
Указать

способ перехода от одного опорного решения к другому, на котором значение целевой функции будет ближе к оптимальному, т.е. указать способ улучшения опорного решения;
Задать критерии, которые позволяют своевременно прекратить перебор опорных решений на оптимальном решении или сделать заключение об отсутствии оптимального решения.
Слайд 5Для того, чтобы решить задачу симплексным методом необходимо выполнить следующий алгоритм:
Привести задачу

к каноническому виду;
Найти начальное опорное решение с "единичным базисом" (если опорное решение отсутствует, то задача не имеет решение ввиду несовместимости системы ограничений);
Вычислить оценки разложений векторов по базису опорного решения и заполнить таблицу симплексного метода;
Если выполняется признак единственности оптимального решения, то решение задачи заканчивается;
Если выполняется условие существования множества оптимальных решений, то путем простого перебора находят все оптимальные решения.
Слайд 6Симплекс-метод включает в себя целую группу алгоритмов и способов решения задач линейного

программирования. Один из таких способов, предусматривающий запись исходных данных и их пересчет в специальной таблице, носит наименование табличного симплекс-метода.
Рассмотрим алгоритм табличного симплекс-метода на примере решения производственной задачи, которая сводится к нахождению производственного плана обеспечивающего максимальную прибыль.
Слайд 7Исходные данные для решения задачи симплекс-методом:
Предприятие выпускает 4 вида изделий, обрабатывая их

на 3-х станках. Нормы времени (мин./шт.) на обработку изделий на станках, заданы матрицей A:
Слайд 8Фонд времени работы станков (мин.) задан в матрице B:
Прибыль от продажи каждой

единицы изделия (руб./шт.) задана матрицей C:
Целью данной задачи является составление такого плана производства, при котором прибыль предприятия будет максимальной.
Слайд 9Проводим вычисления с помощью табличного симплекс-метода:
Обозначим X1, X2, X3, X4 планируемое количество

изделий каждого вида. Тогда искомый план: (X1, X2, X3, X4)
Запишем ограничения плана в виде системы уравнений:
Слайд 103. Тогда целевая прибыль:
То есть прибыль от выполнения производственного плана должна быть

максимальной.
Слайд 114. Для решения получившейся задачи на условный экстремум, заменим систему неравенств системой

линейных уравнений путем ввода в нее дополнительных неотрицательных переменных (X5, X6, X7).
Слайд 125. Примем следующий опорный план:
X1 = 0, X2 = 0, X3

= 0, X4 = 0, X5 = 252, X6 = 144, X7 = 80
6. Занесем данные в симплекс-таблицу:
! В последнюю строку заносим коэффициенты при целевой функции и само ее значение с обратным знаком;
Слайд 137. Выбираем в последней строке наибольшее (по модулю) отрицательное число.
Вычислим b
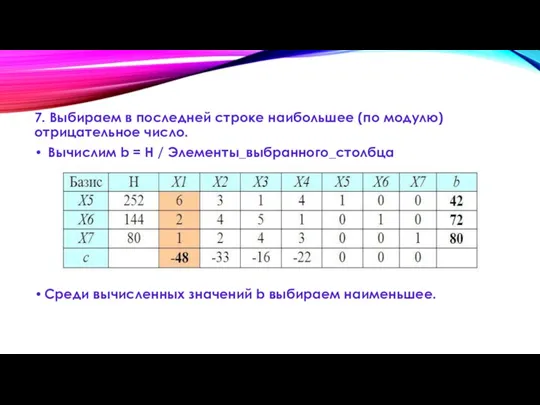
= Н / Элементы_выбранного_столбца
Среди вычисленных значений b выбираем наименьшее.
Слайд 14Пересечение выбранных столбца и строки даст нам разрешающий элемент. Меняем базис на
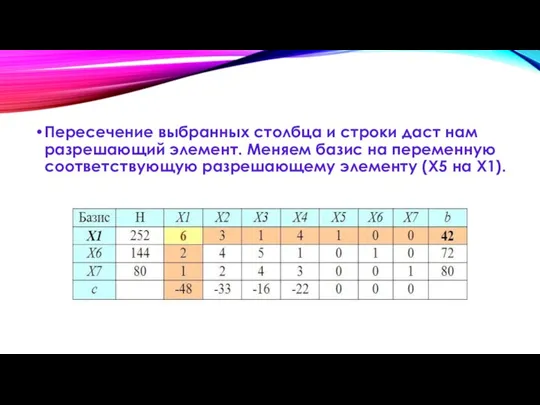
переменную соответствующую разрешающему элементу (X5 на X1).
Слайд 158. Теперь необходимо пересчитать все элементы симплекс-таблицы, кроме столбца b. Вот как

это можно сделать:
Сам разрешающий элемент обращается в 1.
Для элементов разрешающей строки – aij(*) = aij / РЭ (то есть каждый элемент делим на значение разрешающего элемента и получаем новые данные).
Для элементов разрешающего столбца – они просто обнуляются.
Остальные элементы таблицы пересчитываем по правилу прямоугольника.
Слайд 16AIJ(*) = AIJ – ( A * B / РЭ )
Берем текущую
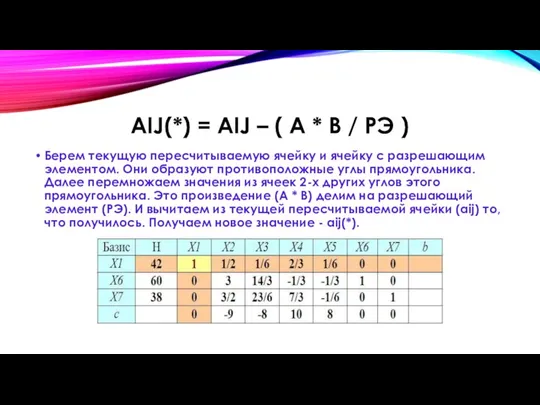
пересчитываемую ячейку и ячейку с разрешающим элементом. Они образуют противоположные углы прямоугольника. Далее перемножаем значения из ячеек 2-х других углов этого прямоугольника. Это произведение (A * B) делим на разрешающий элемент (РЭ). И вычитаем из текущей пересчитываемой ячейки (aij) то, что получилось. Получаем новое значение - aij(*).
Слайд 179. Вновь проверяем последнюю строку (c) на наличие отрицательных чисел. Если их
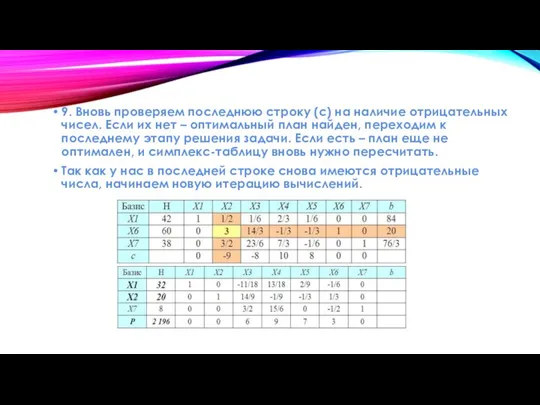
нет – оптимальный план найден, переходим к последнему этапу решения задачи. Если есть – план еще не оптимален, и симплекс-таблицу вновь нужно пересчитать.
Так как у нас в последней строке снова имеются отрицательные числа, начинаем новую итерацию вычислений.
Слайд 1810. Так как в последней строке нет отрицательных элементов, это означает, что

нами найден оптимальный план производства! А именно: выпускать мы будем те изделия, которые перешли в колонку «Базис» - X1 и X2. Прибыль от производства каждой единицы продукции нам известна (матрица C). Осталось перемножить найденные объемы выпуска изделий 1 и 2 с прибылью на 1 шт., получим итоговую (максимальную!) прибыль при данном плане производства.
ОТВЕТ:
X1 = 32 шт., X2 = 20 шт., X3 = 0 шт., X4 = 0 шт.
P = 48 * 32 + 33 * 20 = 2 196 руб.

















 Информационные системы
Информационные системы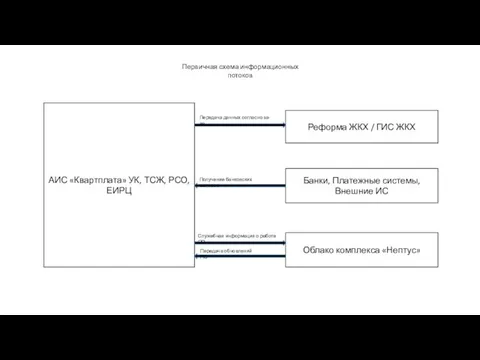 Первичная схема информационных потоков
Первичная схема информационных потоков Построение типовой модели нарушителя безопасности в коммерческой организации
Построение типовой модели нарушителя безопасности в коммерческой организации Ассортиментная идентификация продовольственных товаров
Ассортиментная идентификация продовольственных товаров Составной оператор
Составной оператор Как можно задать значение переменной? Оператор присваивания
Как можно задать значение переменной? Оператор присваивания Презентация на тему Текстовая информация
Презентация на тему Текстовая информация  Математическое моделирование
Математическое моделирование Продающий или непродающий
Продающий или непродающий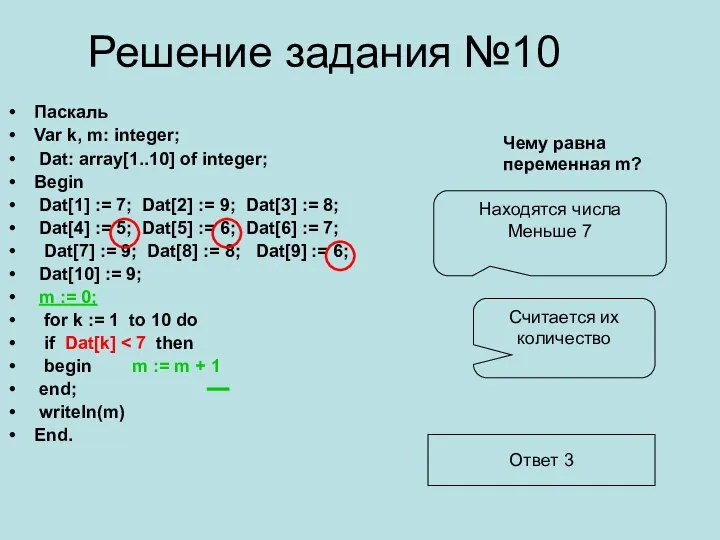 Решение задания №10. Паскаль
Решение задания №10. Паскаль Компьютерные вирусы
Компьютерные вирусы Регистрация и установка программы Adobe Creative Cloud
Регистрация и установка программы Adobe Creative Cloud Гибридные криптосистемы защиты информации
Гибридные криптосистемы защиты информации Графический редактор
Графический редактор Лекция №1.Основные понятия теории баз данных
Лекция №1.Основные понятия теории баз данных Prezentatsia_EVM
Prezentatsia_EVM Архитектура ПК лекция
Архитектура ПК лекция Интенсив. Слепой метод набора
Интенсив. Слепой метод набора Использование ИКТ на уроках изобразительного и декоративно-прикладного искусства
Использование ИКТ на уроках изобразительного и декоративно-прикладного искусства Описание проблемы в СЭД
Описание проблемы в СЭД Витраж. Алгоритм
Витраж. Алгоритм Сборник Adobe Photoshop CS5 для начинающих
Сборник Adobe Photoshop CS5 для начинающих Занятия ОПИ Интернет-промотирование
Занятия ОПИ Интернет-промотирование Что такое токен чата?
Что такое токен чата? Основы ПИКГ. Программы AutoCAD SketchUP
Основы ПИКГ. Программы AutoCAD SketchUP Использование основных методов информатики и средств ИКТ при анализе процессов в обществе, природе и технике
Использование основных методов информатики и средств ИКТ при анализе процессов в обществе, природе и технике Готовимся к экзамену №1. Разбираем типовые ошибки
Готовимся к экзамену №1. Разбираем типовые ошибки Онлайн образование с применением машинного обучения
Онлайн образование с применением машинного обучения