Асимметричное шифрование. Лекция 4

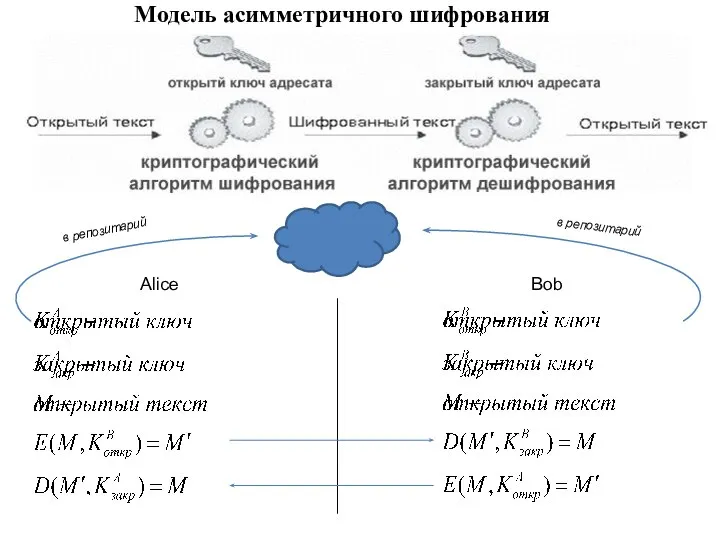
Модель асимметричного шифрования
Alice
Bob
в репозитарий
в репозитарий

Историческая справка и особенности
Шифрование с открытым ключом было открыто двумя американцами, Диффи (Diffie) и Хеллманом (Hellman), в 1976 г
Два ключа, не нужно передавать ключ
Математический аппарат вместо перестановок и подстановок
Различные области применения
Основаны на вычислительно сложных математических задачах

Алгоритм шифрования RSA (Rivest, Shamir и Adleman)
Предложен 1977 году в мат. журнале
Основывается на вычислительной сложности задачи факторизации больших целых чисел
С 1993 года объявлен в стандарте PKCS1 v. 1.5
Блочный шифр
Широко исследован, считается абсолютно надежным при длине ключа больше 2048 бит
Применяется как для шифрования, так и для цифровой подписи

Вспомогательные понятия
Делитель числа n – число которое делит n без остатка.
Простые числа – которые делятся без остатка только на себя и на единицу.
НОД(m,n) – наибольший общий делитель чисел m, n – наибольшее число которое делит без остатка n и т.
НОД(70,105)=35, НОД(5,35)=5
НОД(1678,49)=?

Алгоритм шифрования RSA. Создание пары ключей
Выбираются два простых числа p и q
Вычисляется их произведение n = p*q, n – модуль шифрования
Выбирается произвольное число е (e
НОД(e,(p-1)(q-1)) = 1
Т.е. е должно быть взаимно простым с числом (p-1)(q-1).
4. Находится d – взаимообратное с e по mod (p-1)(q-1).
Для этого решается методом Евклида в целых числах уравнение
e*d+(p-1)(q-1)*y = 1, d и y – неизвестные.
5. Два числа (e, n) публикуются как открытый ключ.
6. Число d является закрытым (секретным) ключом.

Алгоритм шифрования RSA. Шифрование/дешифрование.
Отправитель разбивает M на блоки, меньшие n.
M’ = Мe (mod n) (возводим М в степень е, делим на n и берем целый остаток от деления – это и есть зашифрованный результат)
Шифрование:
M = M’d mod n
Дешифрование:

1. Выбрали простые числа p=7 q=17.
2. Вычислили n = p*q = 7*17 = 119.
3. Вычислили e = 5.
4. Вычислили d = 77 (5*77=1 mod 96)
5. M = 19.
6. Результат шифрования вычисляется так:
195 = 2476099 / 119 = 20807 c остатком 66.
M’ = 195 mod 119=66
Алгоритм шифрования RSA. Пример.
Шифрование:
Дешифрование:
6677 = 1,27*10140 /119 = 1.06*10138 c остатком 19.
M = 6677 mod 119= 19.

Алгоритм Евклида.
Дано a, b задача - найти НОД(a,b).
Пусть a=1071, b=462.
Для любых a и b можно выполнить: a=b*q+r
1071=462*2+147
462=147*3+21
147=21*7+0
НОД(1071, 462)=21

Алгоритм Евклида. Пример 2.
Пусть a=665, b=548.
Для любых a и b можно выполнить: a=b*q+r
665=548*1+117
…
НОД(665, 548)=?

Алгоритм Евклида. Пример 2.
Пусть a=665, b=548.
Для любых a и b можно выполнить: a=b*q+r
665=548*1+117
548=117*4+80
117=80*1+37
80=37*2+6
37=6*6+1
НОД(665, 548)=1

Нахождение коэффициентов Безу
a*x+b*y=НОД(a,b) – соотношение Безу, a и b всегда существуют
следовательно:
если a и b взаимно простые, то уравнение
a*x+b*y=1 всегда имеет решение.

Расширенный алгоритм Евклида. Пример 1.
51*d=1 mod 110, задача - найти d. Для этого решим уравнение:
110*x+51*y=1 (d=y)
110*(-19)+51*y=1
y = 41
Проверка: 51*41=2091=1 mod 110

Расширенный алгоритм Евклида. Пример 2.
17*d=1 mod 77, задача - найти d. Для этого решим уравнение:
77*x+17*y=1 (d=y)
77*2+17*y=1
y = -9=68 mod 77
Проверка: 17*68=1156=1 mod 77
77=17*4+9
17=9*1+8
9=8*1+1

Расширенный алгоритм Евклида. Пример 3.
79*d=1 mod 196, задача - найти d. Для этого решим уравнение:
196*x+79*y=1 (d=y)
y =?
196=79*2+38