Слайд 2КООРДИНАТНЫЕ ПРЕДСТАВЛЕНИЯ
Для создания изображения с помощью программного пакета необходимо задать геометрическое описание

объекта, который следует изобразить. Это описание определяет положение и форму объекта. Например, прямоугольник задается через положение его углов(граней), а сфера – через положение центра и радиус. В программных пакетах общего назначения необходимо, чтобы геометрическое описание задавались в стандартной правосторонней системе координат. Если значения координат рисунка задаются в какой-либо другой системе координат (сферической, гиперболической и т.д.), то, прежде чем вводить их значения в программный пакет, их необходимо преобразовать в декартовы координаты.
В общем случае в процесса создания и изображения сцены используется несколько различных декартовых координатных систем. Во-первых, можно задавать формы отдельных объектов в отдельной системе координат для каждого объекта.
Слайд 3КООРДИНАТНЫЕ ПРЕДСТАВЛЕНИЯ
Такие системы координат называют координатами моделирования, локальными или главными координатами. Задав

формы отдельных объектов, можно составить сцену путем расстановки объектов по соответствующим местам в системе координат сцены, которая называется внешней системой координат. Этот этап подразумевает преобразование отдельных систем координат моделирования в координаты с заданным положением и ориентацией относительно внешней системы координат. Для описания не слишком сложных сцен часть объектов можно добавлять непосредственно в общую структуру сцены во внешних координатах. Геометрическое описание в системе координат моделирования и во внешней системе координат могут задаваться в любой удобной форме, как целые числа или как числа с плавающей точкой, без учета ограничений для отдельных устройств ввода.
Слайд 4КООРДИНАТНЫЕ ПРЕДСТАВЛЕНИЯ
После того, как заданы все элементы сцены, чтобы создать изображение, общее

описание во внешних координатах обрабатывают различными программами в одной или нескольких системах координат устройств ввода. Этот процесс называется конвейером наблюдения (viewing pipeline). Вначале внешнею координаты преобразуются в координаты наблюдения, соответствующие тому изображению сцены, которое мы хотим увидеть. В основе этой системы координат лежит положение и ориентация гипотетической камеры. После этого координаты объекта преобразуются в двумерную проекцию сцены, которая соответствует тому, что мы увидим на устройстве вывода. Затем эта сцена записывается в нормированных координатах, где значение каждой координаты попадает в диапазон от – до 1 или от 0 до 1, в зависимости от системы. Нормированные координаты еще называют нормированными координатами прибора, т.к. такое описание делает графический пакет независимым от диапазона координат специального устройства вывода.
Слайд 5КООРДИНАТНЫЕ ПРЕДСТАВЛЕНИЯ
Еще необходимо определить видимые поверхности и обрезать части рисунка, выходящие за

пределы поля зрения. Наконец, стандарты развертки рисунка преобразовываются и попадают в буфер регенерации растровой системы, чтобы превратится в изображение.. Систему координат устройства изображения обычно называют координатами устройства или экранными координатами. Часто и нормированные координаты и координаты экрана описываются в левосторонней системе координат, так что увеличение положительного расстояния от плоскости OXY (экрана или плоскости изображения) можно интерпретировать как удаление от точки наблюдения.
Слайд 6СИСТЕМЫ КООРДИНАТ
Для того, чтобы, к примету, прорисовать прямолинейный отрезок, необходимо задать положение

его двух концов, а для прорисовки многоугольника необходимо задать набор координат его вершин. Значения координат этих точек хранятся в описании сцены вместе с остальной информацией об этих объектов, таких как цвет и координатных границы, т.е. минимальные и максимальные значения координат x, y, z для каждого объекта. Набор координатных границ называют также ограничивающим прямоугольником данного объекта. Затем объекты изображаются – информация о сцене передаются стандартным процедурам визуализации, которые определяют видимые поверхности и, в конечном итоге, ставят в соответствие объектам значения координат на экране. Для записи информации о сцене, такой как коды цвета, в определенные места буфера кадров используется процесс преобразования в стандарт развертки, и на устройстве вывода изображаются сцены.
Слайд 7ЭКРАННЫЕ КООРДИНАТЫ
Местоположение на экране выражается через целочисленные экранные координаты, которые соответствуют положениям

пикселей в буфере кадра. Значения координат пикселей дают номер строки развертки (значение координаты у) и номер столбца (значение координаты х). При аппаратном выполнении таких процессов, как обновление экрана, как правило, положение пикселей отсчитывается от левого верхнего угла экрана. Тогда строкам развертки присваиваются значения от 0 (верхняя строка экрана) до какого-то целочисленного значения ymax (нижняя строка экрана), а положение пикселей в каждой строке развертки нумеруются от 0 до хmax в направлении слева направо. В то же время с помощью программных команд можно задать любую систему отсчета положений на экране. Например, можно задать диапазон точек с целочисленными координатами и началом координат в нижнем левом углу экрана или воспользоваться для описания рисунка нецелочисленными декартовыми координатами. Затем значения координат, используемых для описания геометрии сцены, с помощью стандартных процедур визуализации преобразуются в целые значения положений пикселей в буфере кадра.
Слайд 8ЭКРАННЫЕ КООРДИНАТЫ
В алгоритмах для строк развертки графические примитивы задаются через координаты представления,

т.е. определяются положения пикселей, которые следует изображать. Например, если заданы координаты конечных точек линейного отрезка, алгоритм построения изображения должен вычислить положения тех пикселей, которые лежат на прямой, соединяющей точки. Так как пиксель занимает конечную площадь экрана, это должно учитываться при выполнении алгоритмов. В настоящее время центр области, занимаемой пикселем, принято сопоставлять с каждым целочисленным значением координаты на экране.
Определив положение пикселей для данного объекта, в буфер кадра необходимо записать соответствующие коды цвета. Чтобы сделать это, предположим, дана низкоуровневая процедура вида
setPixel (x ,y, color); setPixel (x ,y);
Эта функция задает цвет пикселя в изображении с координатами (x , y) относительно произвольно выбранного на экране начала отсчета.
Слайд 9АБСОЛЮТНЫЕ И ОТНОСИТЕЛЬНЫЕ КООРДИНАТЫ
Рассмотренные выше системы координат формулировались через значения абсолютных координат.

Т.е. задается действительное положение точек в используемой системе координат.
Но в некоторых графических пакетах положения точек можно также задавать с помощью относительных координат. Такой способ удобен для построения чертежей с помощью перьевых графопостроителей, создания художественных изображений, а также для издательских целей и печатной работы. Воспользовавшись этим способом, можно задавать координаты точки относительно последнего положения, к которому обращалась система (к текущему положению). Например, если точка с координатами (3,8) - последнее положение, к которому обращалась программа, то относительные координаты (2,-1) соответствуют абсолютным координатам (5,7). В таком случае, перед тем, как задать какие-либо координат для функции примитива, используется дополнительная функция, устанавливающая текущее положение.
Слайд 10АБСОЛЮТНЫЕ И ОТНОСИТЕЛЬНЫЕ КООРДИНАТЫ
Тогда, чтобы описать такой объект, как набор соединенных между

собой прямолинейных отрезков, нужно задать только последовательность относительных координат (смещений) после того, как будет установлено исходное положение. Графические системы могут предлагать опции, для задания положения точки с помощью относительных/ абсолютных координат. Далее будем считать, что все координаты задаются в абсолютных системах отсчета.
В нашей первой программе мы использовали команду
void gluOrtho2D(GLdouble left, GLdouble right, GLdouble bottom, GLdouble top)
Которая представляет функцию, используемую для задания любой двумерной декартовой системы координат. Аргументы этой функции – значения, определяющие границы изменения координат х и у для того рисунка, который требуется изобразить. Т.к. gluOrtho2D описывает ортогональную проекция, необходимо убедится в том, что значения координат помещены в проекционную матрицу OpenGL. Кроме того, перед определением диапазона внешних координат в качестве проекционной матрицы можно использовать единичную матрицу. Это гарантирует, что значения координат не будет прибавляться к значениям,
Слайд 11АБСОЛЮТНЫЕ И ОТНОСИТЕЛЬНЫЕ КООРДИНАТЫ
которые, возможно, были ранее внесены в проекционную матрицу. Таким

образом, систему координат для использованных ранее примеров можно задать с помощью операторов:
glMatrixMode (GL_PROJECTION); // определяем вид матрицы
glLoadIdentity (); // устанавливаем текующую матрицу единичной
gluOrtho2D ( xmin , xmax , ymin , ymax ); // устанавливаем размеры плоскости
При этом левый нижний угол на экране будет описываться координатами ( xmin , уmin), а правый верхний угол – координатами (xmax , ymax ).
После этого можно задать один или несколько графических примитивов, при изображении которых используется система координат, описанная в gluOrtho2D . Если размеры этих примитивов будут вписываться в координатные пределы окна на экране, то будут изображены все примитивы. В противном случае будут видны только те части примитивов, которые попадают в диапазон координат окна. Кроме того, при задании геометрического описания рисунка все координаты примитивов OpenGL должны выражаться в абсолютной системе координат относительно системы отсчета.
Слайд 12ФУНКЦИИ ТОЧЕК В OPENGL
Чтобы описать геометрия точки, ее положение задается во внешней

системе координат. Затем эти значения вместе с другими геометрическими параметрами, которые могут описывать данную сцену, обрабатываются стандартными процедурами визуализации. Пока не заданы другие значения атрибутов, примитивы OpenGL будут изображаться с размерами и цветом, определенными по умолчанию. Изначально цвет примитивов – белый, а размер точки равен размеру одного пикселя на экране.
Чтобы задать координаты единственной точки, используется следующая функция OpenGL:
glVetrex*();
* означает, что для данной функции необходимо указать индексные коды, обозначающие размерность пространства, тип числовых данных, которые используются в качестве значения координат, и возможность представления координат в виде вектора. Функция glVetrex должна находится в программе между функциями glBegin и glEnd. Аргумент glBegin определяет тип графического примитива, который следует изобразить, а функция glEnd не требует аргументов.
Слайд 13ФУНКЦИИ ТОЧЕК В OPENGL
При выводе на экран точки аргументов функции glBegin является

символьная константа GL_POINTS. Таким образом, положение точки в OpenGL описывается так:
glBegin ( GL_POINTS );
glVertex* ();
glEnd ();
Хотя термином Vertex(вершина) в строгом смысле называют «угловую» точку многоугольник, точку пересечения сторон угла, точку пересечения эллипса с его главной осью или другие подобные точки геометрических фигур, функция glVertex описывает положение любой точки. Таким образом, для задания точек, прямых линий и многоугольников применяется одна функция, а для описания объектов, составляющих сцену, чаще всего используются прямоугольные участки.
Координаты точек в OpenGL могут задаваться в двух, трех или четырех измерениях. Для определения размерности используемого пространства необходимо указать индекс 2, 3 или 4 в функции glVertex. Четырехмерное описание указывает на представление с помощью однородных координат, где однородный параметр h (четвертая координата) – масштабный коэффициент для декартовый координат.
Слайд 14ФУНКЦИИ ТОЧЕК В OPENGL
Далее необходимо обозначить, какой тип данных используется для описания

числовых значений координат. Это осуществляется с помощью второго индекса функции glVertex: i (integer), s (short), f (float), d( double).Значения координат в функции glVertex могут перечисляться в явном виде, или может использоваться единственный аргумент, который задает положения координат в виде массива. Если применяется описание координат в виде массива, то необходимо также добавить третий индекс v (vector).
Допустим, необходимо вывести на экран три точки на одинаковом расстоянии друг от друга на двумерном прямолинейном отрезке с тангенсом угла наклона 2:
glBegin ( GL_POINTS );
glVetrex2i ( 50 , 100 );
glVetrex2i ( 75 , 150 );
glVetrex2i ( 100 , 200 );
glEnd ();
Или можно сделать все то же самое, но определить координаты в виде массивов и использовать их вместо параметра функции прорисовки:
Слайд 15ФУНКЦИИ ТОЧЕК В OPENGL
int point1[] = 50,100;
int point2[] = 75,150;
int point3[] =
![ФУНКЦИИ ТОЧЕК В OPENGL int point1[] = 50,100; int point2[] = 75,150;](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1011166/slide-14.jpg)
100,200;
…..
glBegin ( GL_POINTS );
glVetrex2iv ( point1 );
glVetrex2iv ( point2 );
glVetrex2iv ( point1 );
glEnd ();
А вот пример задания двух точек в трехмерном пространстве:
glBegin ( GL_POINTS );
glVetrex3f ( -78.05 , 909.72 , 14.60 );
glVetrex3f ( 261.91, -5200.67, 188.33);
glEnd ();
Кроме того, для описания координат точек можно определить класс или структуру:
Слайд 16ФУНКЦИИ ТОЧЕК В OPENGL
Struct points
{
Glfloat x, y;
}
…
Points pointPos;
pointPos.x = 120.75;
pointPos.y = 45.30;
glBegin

( GL_POINTS );
glVetrex2f (pointPos.x , pointPos.y );
glEnd ();
Слайд 17ФУНКЦИИ ПРЯМЫХ В OPENGL
В графических пакетах, как правило, предлагаются функции для описания

одного или нескольких прямолинейных участков, причём каждый из этих участков определяется координатами двух его концов. В пакете OpenGL координаты одного конца выбирают с помощью glVertex, точно также, как это делалось для координат точки, а в среду glBegin\glEnd заключается список функций glVetrex. Однако теперь в качестве параметра glBegin используется символьная константа, которая указывает, что данный перечень координат нужно понимать, как координаты концов отрезков. Существует три символьные константы OpenGL, которые можно использовать для определения того, как следует соединять точки данного перечня, чтобы получился набор прямолинейных отрезков. По умолчанию каждая символьная переменная дает изображение сплошных линий белого цвета.
Набор прямолинейных отрезков, соединяющих каждую пару начало-конец из перечня, задается с помощью константы GL_LINES.
Слайд 18ФУНКЦИИ ПРЯМЫХ В OPENGL
glClear(GL_COLOR_BUFFER_BIT);
glColor3f(0, 0, 1.0);
int p1[] = { 9,3 };
int p2[]
![ФУНКЦИИ ПРЯМЫХ В OPENGL glClear(GL_COLOR_BUFFER_BIT); glColor3f(0, 0, 1.0); int p1[] = {](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1011166/slide-17.jpg)
= { 2,1 };
int p3[] = { 4,6 };
int p4[] = { 7,1 };
int p5[] = { 0,3 };
glBegin(GL_LINES);
glVertex2iv(p1);
glVertex2iv(p2);
glVertex2iv(p3);
glVertex2iv(p4);
glVertex2iv(p5);
glEnd();
glFlush();
Слайд 19ФУНКЦИИ ПРЯМЫХ В OPENGL
glClear(GL_COLOR_BUFFER_BIT);
glColor3f(0, 0, 1.0);
int p1[] = { 9,3 };
int p2[]
![ФУНКЦИИ ПРЯМЫХ В OPENGL glClear(GL_COLOR_BUFFER_BIT); glColor3f(0, 0, 1.0); int p1[] = {](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1011166/slide-18.jpg)
= { 2,1 };
int p3[] = { 4,6 };
int p4[] = { 7,1 };
int p5[] = { 0,3 };
glBegin(GL_LINE_STRIP);
glVertex2iv(p1);
glVertex2iv(p2);
glVertex2iv(p3);
glVertex2iv(p4);
glVertex2iv(p5);
glEnd();
glFlush();
Слайд 20ФУНКЦИИ ПРЯМЫХ В OPENGL
glClear(GL_COLOR_BUFFER_BIT);
glColor3f(0, 0, 1.0);
int p1[] = { 9,3 };
int p2[]
![ФУНКЦИИ ПРЯМЫХ В OPENGL glClear(GL_COLOR_BUFFER_BIT); glColor3f(0, 0, 1.0); int p1[] = {](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1011166/slide-19.jpg)
= { 2,1 };
int p3[] = { 4,6 };
int p4[] = { 7,1 };
int p5[] = { 0,3 };
glBegin(GL_LINE_LOOP);
glVertex2iv(p1);
glVertex2iv(p2);
glVertex2iv(p3);
glVertex2iv(p4);
glVertex2iv(p5);
glEnd();
glFlush();
Слайд 21АЛГОРИТМЫ ПОСТРОЕНИЯ ПРЯМЫХ В OPENGL
Прямолинейный отрезок на сцене определяется координатами его концов.

Чтобы изобразить прямую на растровом мониторе, графическая система сперва должна спроектировать положения концов отрезка, переводя их в целочисленные значения экранных координат, и определить ближайшие положения пикселей, лежащих вдоль линии, соединяющей эти концы. Затем в буфер кадра загружается цвет линии с соответствующими координатами пикселей. Считывая информацию из буфера кадра, видеоконтроллер изображает пиксели на экране. В ходе этого процесса происходит цифровая обработка прямой линии и преобразование ее а целочисленные значения координат, которые в общем случае только приблизительно передают настоящую форму линии. Рассчитанные координаты прямой (10.48 ; 20.51) дают координаты пикселя (10; 21). Такое округление значений координат до целых чисел приводит к тому, что все линии, кроме горизонтальных и вертикальных, изображаются в виде «зубцов».
Слайд 22АЛГОРИТМЫ ПОСТРОЕНИЯ ПРЯМЫХ В OPENGL
Характерная «зубчатость» особенно заметна в системах с невысоким

разрешением. Их внешний вид можно несколько улучшить с помощью систем с высокой разрешающей способностью. Более эффективные методы сглаживания растровых линий основываются на подборе интенсивности пикселей, находящихся на этой линии.
Слайд 23АЛГОРИТМЫ ПОСТРОЕНИЯ ПРЯМЫХ В OPENGL. УРАВНЕНИЕ ПРЯМОЙ
Положение пикселей вдоль прямой линии определяется

исходя из геометрических свойств прямой линии. Декартово уравнение прямой линии имеет вид
y = a * x + b (1)
где a – тангенс угла наклона прямой, b – точка ее пересечения с осью ординат. Если известно, что два конца отрезка заданы как точки с координатами (x0 , y0) и (xend , yend), то можно найти значения тангенса угла наклона a и точки b пересечения с осью y по следующим формулам:
(2)
(3)
Алгоритмы изображения прямых линий основаны на уравнении прямой и на последних двух формулах.
Слайд 24АЛГОРИТМЫ ПОСТРОЕНИЯ ПРЯМЫХ В OPENGL. УРАВНЕНИЕ ПРЯМОЙ
Для любого заданного интервала координат x(∂x)

вдоль линии из уравнения (2) можно найти соответствующий интервал координат y(∂y):
∂y = a * x(∂x) (4)
Аналогично можно найти интервал оси x(∂x), соответствующий заданному ∂у:
(5)
Эти уравнения составляют основу для определения отклоняющих напряжений в твких аналоговых дисплеях, как системы векторного сканирования, где возможны относительно небольшие изменения величины отклоняющего напряжения. Для прямых с тангенсом угла | a| < 1 ∂x может устанавливаться пропорциональным небольшому горизонтальному отклоняющему напряжению, и тогда соответствующее вертикальное отклонение задается пропорционально ∂у, что можно рассчитать по формуле (4). Для прямых, тангенс угла которых больше 1, ∂у можно выбирать пропорционально небольшому вертикальному отклоняющему напряжению, при этом соответствующее горизонтальное отклонение
Слайд 25АЛГОРИТМЫ ПОСТРОЕНИЯ ПРЯМЫХ В OPENGL. УРАВНЕНИЕ ПРЯМОЙ
Задается пропорционально ∂х, которое рассчитывается по

формуле (5). Для прямых с тангенсом наклона угла, равным 1 и ∂у= ∂х, и напряжения горизонтального и вертикального отклонения равны между собой. В каждом из этих случаев между заданными точками изображается гладкая прямая с тангенсом угла наклона a.
В растровых системах прямые линии строятся по пикселям, и размер шага в горизонтальном и вертикальном направлении ограничивается разрешением пикселей. Это значит, что нужно «провести выборку» точек прямой линии с дискретными значениями и определить пиксели, самые близкие к данным прямой для каждого элемента выборки. Этот процесс отражен на рисунке, где элементы выборки с дискретными координатами расположены вдоль оси х.
Слайд 26АЛГОРИТМЫ ПОСТРОЕНИЯ ПРЯМЫХ В OPENGL. АЛГОРИТМ ЦДА
Цифровой дифференциальный анализатор (ЦДА) = алгоритм

преобразования стандартов развертки прямой линии, основанный на вычислении либо ∂x, либо ∂у по уравнениям (4) или (5). Прямая разбивается на единичные отрезки по одной из координат, а для другой координаты определяются соответствующие целые значения, ближайшие к данной прямой.
Рассмотрим прямую линию с положительным тангенсом угла наклона.
Слайд 27АЛГОРИТМЫ ПОСТРОЕНИЯ ПРЯМЫХ В OPENGL. АЛГОРИТМ ЦДА
Если тангенс угла наклона меньше или

равен 1, прямая разбивается на единичные отрезки по координате х (∂x = 1), и последовательно вычисляются значения у:
(6)
Индекс k пробегает целые числа от 0 (первая точка) и увеличивается на 1 доя тех пор, пока не будет достигнута последняя точка. Поскольку a может быть любым действительным числом от 0 до 1, каждое рассчитанное значение следует округлять до ближайшего целого числа, соответствующего положению пикселя на экране в обрабатываемом столбцу х.
Для прямых с положительным тангенсом угла наклона, превышающим 1, координаты х и у необходимо поменять местами. Прямая разбивается на единичные отрезки по у (∂у = 1) и последовательно вычисляются значения
(7)
Слайд 28АЛГОРИТМЫ ПОСТРОЕНИЯ ПРЯМЫХ В OPENGL. АЛГОРИТМ ЦДА
В основе уравнений (6) и (7)

лежит предположение, что линии обрабатываются в направлении от левого до правого конца. Если обработку выполнять в обратном направлении, то есть слева направо, то либо ∂x = -1 и
(8)
Либо ∂у = -1 и
(9)
Аналогичные вычисления выполняются с помощью формул (6) – (9), что позволяет определить положения пикселей на прямой с отрицательным тангенсом угла наклона. Таким образом, если абсолютное значение тангенса угла наклона меньше 1, а начальная точка находится слева, то полагаем ∂x = 1 и вычисляем значения у с помощью (6), Если начальная точка находится справа, тангенс угла наклона положительный и меньше 1, то полагаем ∂х = -1 и находим положения у с помощь. (8). Для отрицательного тангенса угла наклона с абсолютным значением больше 1 мы используем ∂у = -1 и (9), или ∂у = 1 и (7).
Слайд 29АЛГОРИТМЫ ПОСТРОЕНИЯ ПРЯМЫХ В OPENGL. АЛГОРИТМ ЦДА
Этот алгоритм сведен к следующей процедуре,

входом которой служат 2 целочисленных значения экранных координат концов отрезка. Параметрам dx и dy присваиваем значения горизонтальной и вертикальной разностей между точками-концами отрезков. Большую из разностей обозначаем step. Начиная с координат (х0, у0) определяем смещение, необходимое на каждом шаге для того, чтобы найти следующее положение этой прямой. Этот процесс выполняется step раз. Если dx больше, чем dy, а х0 меньше, чем xend, то значения приростов по направлениям х и у будут равны 1 и а соответственно. Если же разность по координате х больше, но при этом х0 больше, чем xend, то для создания следующей точки на прямой используются декременты -1 и –а. В любом случае, в направлении у используется единичный прирост, а в направлении х – прирост 1/а.
#include
#include
Слайд 30АЛГОРИТМЫ ПОСТРОЕНИЯ ПРЯМЫХ В OPENGL. АЛГОРИТМ ЦДА
void init(void)
{
glClearColor(0, 0, 0, 0.0);
glMatrixMode(GL_PROJECTION);
gluOrtho2D(0.0, 20.0,

0.0, 15.0);
}
void setPixel(int x, int y)
{
glBegin(GL_POINTS);
glVertex2i(x, y);
glEnd();
glFlush();
}
Слайд 31АЛГОРИТМЫ ПОСТРОЕНИЯ ПРЯМЫХ В OPENGL. АЛГОРИТМ ЦДА
inline int round_k(const float a)
{
return int(a

+ 0.5);
}
void lineCDA(int x0, int y0, int xend, int yend)
{
int dx = xend - x0, dy = yend - y0, step, k;
float xInc, yInc, x = x0, y = y0;
step = (abs(dx) > abs(dy)) ? abs(dx) : abs(dy);
xInc = float(dx) / float(step);
yInc = float(dy) / float(step);
Слайд 32АЛГОРИТМЫ ПОСТРОЕНИЯ ПРЯМЫХ В OPENGL. АЛГОРИТМ ЦДА
setPixel(round_k(x), round_k(y));
for (k = 0; k

< step; k++)
{
x += xInc;
y += yInc;
setPixel(round_k(x), round_k(y));
}
}
void myDisplay(void)
{
glClear(GL_COLOR_BUFFER_BIT);
glColor3f(1, 1, 1);
lineCDA(0, 0, 20, 40);
}
Слайд 33АЛГОРИТМЫ ПОСТРОЕНИЯ ПРЯМЫХ В OPENGL. АЛГОРИТМ ЦДА
void main(int argc, char** argv)
{
glutInit(&argc, argv);
glutInitDisplayMode(GLUT_SINGLE

| GLUT_RGB);
glutInitWindowPosition(0, 100);
glutInitWindowSize(400, 300);
glutCreateWindow("Пример ");
init();
glutDisplayFunc(myDisplay);
glutMainLoop();
}
Слайд 34АЛГОРИТМЫ ПОСТРОЕНИЯ ПРЯМЫХ В OPENGL. АЛГОРИТМ ЦДА
Слайд 35АЛГОРИТМЫ ПОСТРОЕНИЯ ПРЯМЫХ В OPENGL. АЛГОРИТМ ЦДА
Алгоритм ЦДА – более быстрый способ

вычисления положений пикселей, чем тот, при котором непосредственно используется уравнения прямой. В нем операция умножения, фигурирующая в уравнении прямой, исключена за счет использования растровых характеристик, так что при перемещении по прямой и переходе от одного пикселя к другому прибавляются нужные приросты по направления х и у. Тем не менее, если отрезки достаточно длинные, то из-за накопления ошибок округления при последовательном прибавлении прироста возможно смещение положения пикселя относительно фиксированного направления прямой. Более того, операции округления и арифметика м плавающей точкой требует больших временных затрат. Выполнение ЦДА алгоритма можно ускорить, разделив приросты а и 1/а на целую и дробную части, чтобы все вычисления сводились к операциям с целыми числами.
Слайд 36АЛГОРИТМЫ ПОСТРОЕНИЯ ПРЯМЫХ В OPENGL. АЛГОРИТМ БРЕЗЕНХЕМА
Алгоритм Брезенхема – точный и эффективный

растровый алгоритм создания прямых линий, в котором вычисляются только целочисленные значения приростов. Кроме того, алгоритм можно адаптировать для изображения окружностей и других кривых.
Рассмотрим процесс преобразования стандартов развёртки для прямой с положительным тангенсом угла наклона, меньше 1. В этом случае положение пикселей на прямой определяется разбиением на единичные отрезки по координате х. Начиная с левого конца (х0, у0) данной прямой, при переходе к соседнему столбцу наносится пиксель, который по своему номеру строки развертки у является самым близким к направлению прямой.
Слайд 37АЛГОРИТМЫ ПОСТРОЕНИЯ ПРЯМЫХ В OPENGL. АЛГОРИТМ БРЕЗЕНХЕМА
Предположим, что мы определили , что

следует наносить пиксель с координатами (xk,yk). Далее необходимо решить, какой пиксель изображать в столбце x(k+1) = xk + 1. Выбор необходимо сделать из пикселей с координатами (xk + 1, yk) (xk + 1, yk + 1).
В точке выборки с координатами xk + 1
обозначим расстояния по вертикали от пик-
селей до математической прямой как
d_lower и d_upper. Координата у математи-
ческой прямой в столбце пикселей xk + 1 на-
ходятся как
у = а * (xk + 1) + b (10)
Тогда
d_lower = y – yk = a * (xk + 1) + b – yk (11)
d_upper = (yk +1) – y = yk +1 - a * (xk + 1) - b
(12)
Чтобы определить, какой из этих пикселей ближе к заданной прямой, можно провести эффективную проверку, основанную на разности двух расстояний до пикселей:
Слайд 38АЛГОРИТМЫ ПОСТРОЕНИЯ ПРЯМЫХ В OPENGL. АЛГОРИТМ БРЕЗЕНХЕМА
d_lower - d_upper = 2 *

а * (xk + 1) – 2 * уk + 2 * b – 1 (13)
Параметр pk - параметр принятия решения для k-ого шага алгоритма построения прямой линии находится путем такого преобразования уравнения (13), чтобы в него входили только целочисленные расчеты. Это можно сделать, проведя подмену a=∂y/ ∂x, где ∂ -вертикальные и горизонтальные расстояния между концами отрезка, и вычислить параметр принятия решения как:
pk = ∂x * ( d_lower – d_upper) = 2 * ∂y * xk – 2 * ∂x * yk +c (14)
Знак параметра pk будет таким же, как и знак d_lower – d_upper. Параметр с – постоянная со значением 2 * ∂y + ∂х * (2 * b -1), которая не зависит от координаты пикселя и находится в ходе рекурсивных вычислений, необходимых для расчета pk . Если пиксель с координатой yk окажется ближе к реальному направлению прямой, чем пиксель с координатой yk+1( т.е. d_lower < d_upper), то параметр принятия решений окажется отрицательным и на график наносится нижний пиксель. Если pk оказывается положительным, то на график наносится верхний пиксель.
Слайд 39АЛГОРИТМЫ ПОСТРОЕНИЯ ПРЯМЫХ В OPENGL. АЛГОРИТМ БРЕЗЕНХЕМА
Изменение значения координаты вдоль направления прямой

происходит при единичном шаге как в направлении х, так и у направлении у. Следовательно, с помощью схемы целочисленного прироста можно найти значения последующих параметров принятия решения. На шаге k+1 параметр находится из уравнения (14) как
pk+1 = 2 * ∂y * (xk+1) – 2 * ∂x * (yk + 1) + c
Вычитая (14) из предыдущего уравнения, получим
pk+1 – pk = 2 * ∂y * ( xk+1 – xk ) – 2 * ∂x * ( yk+1 – yk )
или
pk+1 = pk + 2 * ∂y – 2 * ∂x * ( yk+1 – yk ) (15)
где yk+1 – yk равен или 0 или 1, в зависимости от знака параметра pk.
Такой рекурсивный расчет параметров принятия решения выполняется в каждой точке с целым значением координаты х, начиная с координаты левого конца отрезка. Первый параметр p0 находится из уравнения (14) в начальной точке с координатами ( х0, у0 ), при этом а находится как ∂y/ ∂х:
p0 = 2 * ∂y - ∂х 16)
Итого, при выполнении преобразования стандартов развертки постоянные 2 * ∂y и 2 * ∂y - 2 * ∂х рассчитывается один раз для прямой.
Слайд 40АЛГОРИТМЫ ПОСТРОЕНИЯ ПРЯМЫХ В OPENGL. АЛГОРИТМ БРЕЗЕНХЕМА
Алгоритм Брезенхема
Вводим два конца отрезка, помечая

левый конец отрезка как (х0, у0).
Задаем в буфере кадра цвет пикселя (х0, у0).
Вычисляем постоянные ∂х, ∂y, 2 * ∂y и 2 * ∂y – 2 * ∂х и находим начальное значение параметра принятия решения р0 = 2 * ∂y - ∂х.
Для каждого xk вдоль прямой, начиная с k = 1, проводим проверки: если pk < 0, то следующую точку следует изобразить на месте пикселя (xk+1, yk) и pk+1 = pk + 2 * ∂y. Если pk > 0, то следующую точку следует изобразить на месте пикселя (xk+1, yk+1) и pk+1 = pk + 2 * ∂y – 2 * ∂x .
Выполняем этап ∂x – 1 раз.
Слайд 41АЛГОРИТМЫ ПОСТРОЕНИЯ ПРЯМЫХ В OPENGL. АЛГОРИТМ БРЕЗЕНХЕМА
void linesBrasenhem(int x0, int y0, int

xend, int yend)
{
int dx = abs(xend - x0), dy = abs(yend - y0);
int p = 2 * dy - dx;
int x, y;
if (x0 > xend)
{
x = xend;
y = yend;
xend = x0;
}
else
{
x = x0;
y = y0;
}
Слайд 42АЛГОРИТМЫ ПОСТРОЕНИЯ ПРЯМЫХ В OPENGL. АЛГОРИТМ БРЕЗЕНХЕМА
setPixel(x, y);
}
while (x < xend)
{
x++;
if (p

< 0)
p += 2 * dy;
else
{
y++;
p += 2 * (dy-dx);
}
setPixel(x, y);
}
Слайд 43АЛГОРИТМЫ ПОСТРОЕНИЯ ПРЯМЫХ В OPENGL. АЛГОРИТМ БРЕЗЕНХЕМА
Слайд 44АЛГОРИТМЫ ПОСТРОЕНИЯ ПРЯМЫХ В OPENGL. АЛГОРИТМ БРЕЗЕНХЕМА
Слайд 45АЛГОРИТМЫ ПОСТРОЕНИЯ ПРЯМЫХ В OPENGL. АЛГОРИТМ БРЕЗЕНХЕМА
Алгоритм Брезенхема можно обобщить для прямых

линий с произвольным тангенсом угла наклона, рассмотрев симметрию различных октантов и квадрантов плоскости ху. Для прямой с положительным тангенсом угла наклона, превышающим 1, роли х и у меняются местами. Это означает, что в направлении координаты у делаются единичные шаги, и при этом последовательно вычисляются координаты х, ближайшие к направлению прямой. Кроме того, программу можно изменить таким образом, чтобы построение прямой начиналось с другого конца. Если у качестве исходной точки прямой с положительным тангенсом угла наклона берется правый конец отрезка, то х и у уменьшаются при каждом шаге слева направо. Чтобы гарантировать, что независимо от начальной точки будут изображаться одни и те же пиксели, когда вертикальные расстояния от пикселей до прямой равны ( d_lower = d_upper), всегда выбирается верхний (или нижний) пиксель.
При отрицательном тангенсе угла наклона алгорит аналогичный, только на этот раз одна координата увеличивается, а вторая, наоборот, уменьшается.
Слайд 46АЛГОРИТМЫ ПОСТРОЕНИЯ ПРЯМЫХ В OPENGL. АЛГОРИТМ БРЕЗЕНХЕМА
Наконец, можно отдельно рассматривать некоторые частные

случаи: горизонтальные ( ∂y = 0), вертикальные ( ∂ч = 0), и диагональные прямые (|∂y| = |∂x| ) можно непосредственно заносить в буфер кадров без обработки с помощью алгоритма построения простых линий.
Слайд 47ИЗОБРАЖЕНИЕ ЛОМАНЫХ ЛИНИЙ
Для построения ломаных линий следует n – 1 раз вызвать

процедуру построения прямой линии, в результате чего изображаются прямые линии, соединенные в n точках. При каждом последующем вызове функции сообщается пара наборов координат, необходимых для построения следующего отрезка прямой, причем первой точкой в каждой паре является последняя точка предыдущего отрезка. После того, как в буфер кадра заносится код цвета пикселей, составляющих первый отрезок, обрабатывается следующий, начиная с пикселя, идущего после первого конца этого отрезка. Таким образом можно избежать дублирующего присвоения точкам – концам отрезка кода цвета.
Слайд 48ПАРАЛЛЕЛЬНЫЕ АЛГОРИТМЫ ПОСТРОЕНИЯ ПРЯМЫХ
В рассмотренным ранее методах построения прямых положения пикселей определялись

последовательно. Параллельная же обработка позволяет одновременно рассчитывать положения нескольких пикселей на прямой, распределяя вычисления между различными доступными процессорами.
Одним из способов решения задачи распределения является модификация существующего последовательного алгоритма, позволяющая воспользоваться преимуществами, которые предлагают несколько процессоров. Кроме того, можно придумать другой алгоритм обработки, когда положения пикселей эффективно вычисляются по параллельной схеме. При создании параллельного алгоритма важным вопросом является равномерное распределение задач по обработке данных среди доступных процессоров.
Если доступно np процессоров, параллельный алгоритм построения прямой линии Брезенхема получается путем деления прямой на np частей с созданием отрезков на каждом подинтревале. Для прямой линии с тангенсом угла наклона 0 < a < 1, и координатами левого конца отрезка (х0, у0) прямую можно разделить в положительном направлении оси х. Расстояние между начальными точками соседних частей по координате х определяется следующим образом:
Слайд 49ПАРАЛЛЕЛЬНЫЕ АЛГОРИТМЫ ПОСТРОЕНИЯ ПРЯМЫХ
(17)
где ∂х – длина линии, а длина отрезков

∂хр , на которые разбивается эта линия, вычисляется с помощью целочисленного деления. Пронумеровав полученные части и процессоры от 0 до nр-1, начальную координату k-ого сегмента можно найти как
xk = x0 +k * ∂хp (18)
Допустим, nр = 4, а ∂х = 15. Тогда длина каждого интервала исходной линии будет 4, а координаты начала каждого из них можно определить как х0, х0+4, х0+8, х0+12. Очевидно, что возможна ситуация, когда крайний правый интервал будет короче всех остальных. Также, если координаты концов отрезка будут не целыми числами, то округление может привести к тому, что разные отрезки прямой будут иметь разную длину.
Чтобы применить к этим подинтервалам алгоритм Брезенхема, нужно знать начальное значение координаты у и начальное значение параметра принятия решения для каждого подинтервала. Изменение ∂уp в направлении координаты у для каждого отрезка рассчитывается по наклону прямой а и длине отрезков ∂хp, на которые разбивается прямая
Слайд 50ПАРАЛЛЕЛЬНЫЕ АЛГОРИТМЫ ПОСТРОЕНИЯ ПРЯМЫХ
(19)
Таким образом, для k-ого сегмента начальное значение координаты

e будет равным
yk = y0 + round ( k * ∂уp ) (20)
Исходное значение параметра принятия решения для алгоритма Брезенхема в начале k-ого подинтервала находится из уравнения (14):
pk =2 * ∂y * (k* ∂xp) – round (2 * ∂x * k* ∂yp ) + 2 * ∂у - ∂x (21)
Затем каждый процессор рассчитывает положения пикселей на выделенном ему участке, используя предыдущее значение начального параметра принятия решения и начальные координаты (xk, yk). При определении начальных значений yk и рk вычисления с величинами с плавающей точкой можно свести к арифметическим действиям с целыми числами, выполнив замену a = ∂y/∂x и перегруппировав члены уравнения.
Параллельный алгоритм Брезенхема можно применить и к пряой, тангенс угла наклона которой больше 1, разделив прямую на сегменты по координате у. При отрицательном тангенсе одна из координат увеличивается, а вторая параллельно уменьшается.
Слайд 51ПАРАЛЛЕЛЬНЫЕ АЛГОРИТМЫ ПОСТРОЕНИЯ ПРЯМЫХ
Еще один способ реализации параллельного алгоритма в растровых системах

– соотнести с каждым процессором определенную группу пикселей на экране. При достаточном количестве процессоров с каждым из них можно соотнести один пиксель из какой-то области экрана. Этот подход применяется для изображения прямых, где каждому пикселю в пределах координатных областей заданной прямой ставится в соответствие один процессор и вычисляется расстояние от пикселей до самой прямой. Количество пикселей в ограничивающем прямоугольнике равно ∂х * ∂у . Перпендикулярное расстояние d от прямой до пикселя с координатами (х, у) находится следующим образом
d = A * x + B * y + C (22)
где
причем













![ФУНКЦИИ ТОЧЕК В OPENGL int point1[] = 50,100; int point2[] = 75,150;](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1011166/slide-14.jpg)


![ФУНКЦИИ ПРЯМЫХ В OPENGL glClear(GL_COLOR_BUFFER_BIT); glColor3f(0, 0, 1.0); int p1[] = {](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1011166/slide-17.jpg)
![ФУНКЦИИ ПРЯМЫХ В OPENGL glClear(GL_COLOR_BUFFER_BIT); glColor3f(0, 0, 1.0); int p1[] = {](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1011166/slide-18.jpg)
![ФУНКЦИИ ПРЯМЫХ В OPENGL glClear(GL_COLOR_BUFFER_BIT); glColor3f(0, 0, 1.0); int p1[] = {](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1011166/slide-19.jpg)































 Памятка по использованию телемедицинской платформы
Памятка по использованию телемедицинской платформы Доказательное программирование
Доказательное программирование Презентация на тему Применение телекоммуникаций в современной жизни
Презентация на тему Применение телекоммуникаций в современной жизни  Комплексная Автоматизация TurboFly ERP
Комплексная Автоматизация TurboFly ERP Video Compression
Video Compression Abordări probabiliste Machin Learn
Abordări probabiliste Machin Learn Компьютер как универсальное устройство обработки информации
Компьютер как универсальное устройство обработки информации Взаимосвязь параметров двухзвенной схемы
Взаимосвязь параметров двухзвенной схемы Программирование автоматики
Программирование автоматики ИК Базы данных. Урок 1
ИК Базы данных. Урок 1 Організація пам'яті комп'ютера. Прості схеми управління пам'яттю. Тема 3.1
Організація пам'яті комп'ютера. Прості схеми управління пам'яттю. Тема 3.1 Измерение информации
Измерение информации Маркировка возрастных ограничений в каталогах и фондах библиотек
Маркировка возрастных ограничений в каталогах и фондах библиотек 10 лайфхаков, которые немного упростят жизнь во время работы в ворде
10 лайфхаков, которые немного упростят жизнь во время работы в ворде Ориентированный граф
Ориентированный граф Ромашки. Электронная физминутка для глаз
Ромашки. Электронная физминутка для глаз Язык С.С/С++ (лекция 1)
Язык С.С/С++ (лекция 1) Линейные списки
Линейные списки Схема работы алгоритма DES
Схема работы алгоритма DES Изучение технологии асимметричного шифрования информации и применения электронно-цифровой подписи
Изучение технологии асимметричного шифрования информации и применения электронно-цифровой подписи Информационные носители
Информационные носители Планерка. Семейство IG
Планерка. Семейство IG Мобильное приложение Crazy Color. Проект
Мобильное приложение Crazy Color. Проект StarCraft. Серия научно-фантастических игр в жанре RTS
StarCraft. Серия научно-фантастических игр в жанре RTS Инструкция по работе с Гугл Классом
Инструкция по работе с Гугл Классом Использование цифровых технологий в спорте
Использование цифровых технологий в спорте Оператор множественного выбора САSE
Оператор множественного выбора САSE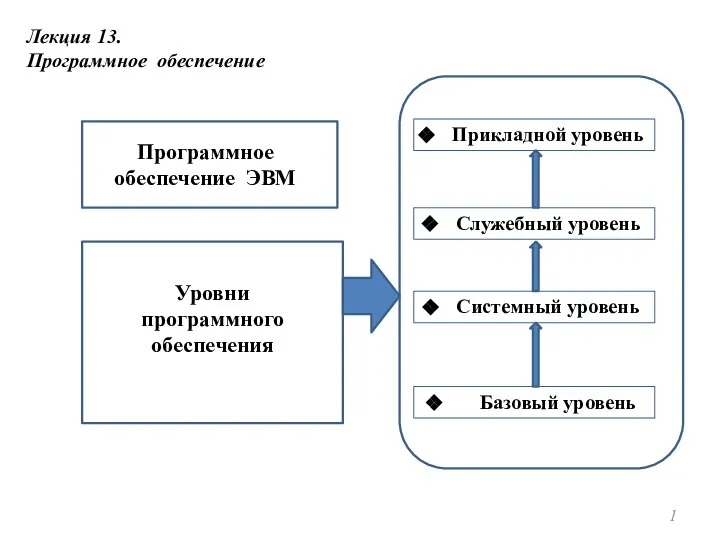 Программное обеспечение
Программное обеспечение