Подходы к измерению информации

Подходы
к измерению информации
Содержательный
с точки зрения человека
Алфавитный
с точки зрения техники

Содержательный подход
Сообщение содержит информацию, если оно новое и понятное.
Сообщение, уменьшающее неопределенность знаний в 2 раза, несёт 1 бит информации.

где
i - количество информации в сообщении,
N – количество равновероятных событий.

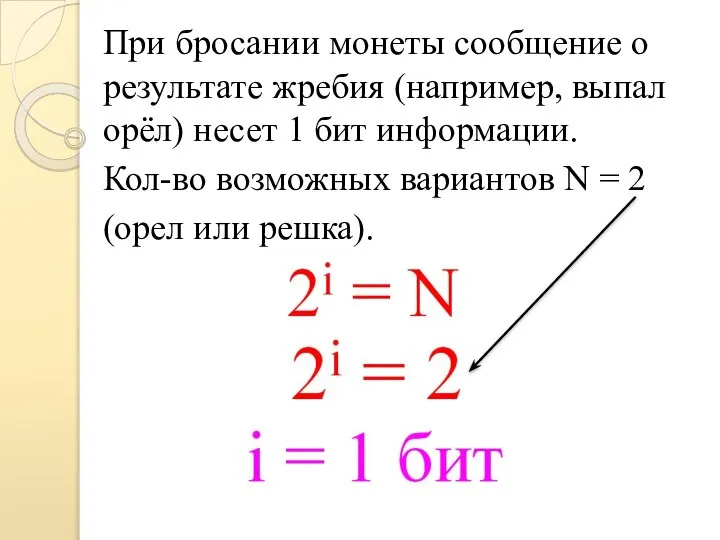
При бросании монеты сообщение о результате жребия (например, выпал орёл) несет 1 бит информации.
Кол-во возможных вариантов N = 2
(орел или решка).

«Вы выходите на следующей остановке?» – спросили человека в автобусе.
«Нет», – ответил он.
Сколько информации содержит ответ?

Какой объем информации
содержит сообщение,
уменьшающее неопределенность знаний в 4 раза?

Задача 1
В барабане для розыгрыша лотереи находится 32 шара. Сколько информации содержит сообщение о первом выпавшем номере.
Решение:
Количество возможных вариантов – 32

Задача 2
В корзине лежат 16 шаров разного цвета. Сколько информации несёт сообщение о том, что из корзины достали красный шар?
Решение:
2 I = N
Здесь N = 16 – число шаров.
Решая уравнение 2 I =16
получаем ответ: I = 4 бита.

Алфавитный подход
Является объективным, т.е. не зависит от субъекта, воспринимающего текст.

Алфавит - множество символов, используемых при записи текста.
Мощность (размер) алфавита (N) - полное количество символов в алфавите.

Количество информации, которое несёт каждый символ, вычисляется по формуле:
I = log2N
В 2-хсимвольном алфавите каждый символ весит 1 бит.
В 4-хсимвольном 2 бита.
В 256-тисимвольном 8 бит.

1 символ занимает 1 байт,
т.е. при вводе символа с клавиатуры, компьютер получает 1 байт информации.
С помощью 1 байта можно закодировать любой из 256 символов алфавита клавиатуры (28=256).

При алфавитном подходе размер содержащейся в ней информации равен:
I=K*i
где i – информационный вес одного символа.
Т.е. чтобы найти количество информации в сообщении надо найти количество символов в нём (в том числе пробелов и знаков препинания) и умножить на 1 байт.

Какое количество информации содержит предложение
Персональный компьютер.

Задача
На странице книги 60 строк
по 56 символов.
Подсчитать количество информации
на данной странице.
(Показать решение):
Количество символов на странице = 60 строк * 56 символов = 3360 символов.
По условию используется 32-х символьный алфавит (т.е. мощность алфавита = 32 символа).
Тогда 2i = 32 символа, отсюда i = 5 бит. Такое количество информации приходится на 1 символ 32-х символьного алфавита.
Количество информации, содержащееся на странице = 3360 символов * 5 бит = 16800 бит.
Переводим в байты: 16800 бит : 8 бит = 2100 байт.
Переводим в Кб 2100 байт : 1024 байт = 2,05 Кб.