Содержание
- 2. Логика Способность к развитому абстрактному мышлению, которая, формируется логикой, и есть то, что отделяет нас от
- 3. Логика Клод Шеннон (1916-2001). Его исследования позволили применить алгебру логики в вычислительной технике Аристотель (384-322 до
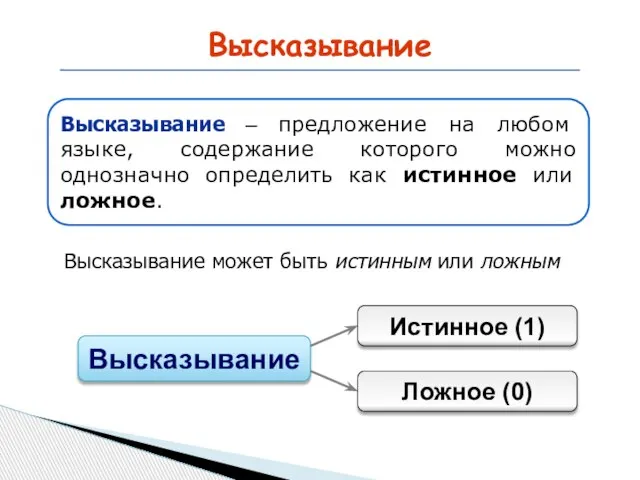
- 4. Высказывание Высказывание может быть истинным или ложным Высказывание Истинное (1) Ложное (0) Высказывание – предложение на
- 5. Высказывание В русском языке высказывания выражаются повествовательными предложениями: Земля вращается вокруг Солнца. Москва - столица. Но
- 6. Примеры высказываний Москва больше Санкт-Петербурга Все мальчики любят играть в футбол “Лед - твердое состояние воды”
- 7. Высказывание Объясните, почему следующие предложения не являются высказываниями. 1) Какого цвета этот дом? 2) Число Х
- 8. Высказывание или нет Зимой идет дождь. Снегири живут в Крыму. Кто к нам пришел? У треугольника
- 9. Алгебра логики Алгебра логики возникла в середине XIX века в трудах английского математика Джорджа Буля. Ее
- 10. Алгебра логики Алгебра логики позволяет определять истинность или ложность составных высказываний, не вникая в их содержание.
- 11. Простые и сложные высказывания Высказывания могут быть простыми или сложными. Сложные высказывания состоят из простых высказываний,
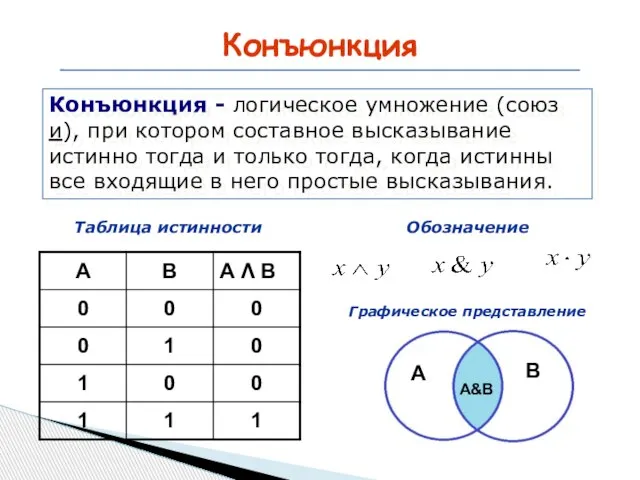
- 12. Конъюнкция Конъюнкция - логическое умножение (союз и), при котором составное высказывание истинно тогда и только тогда,
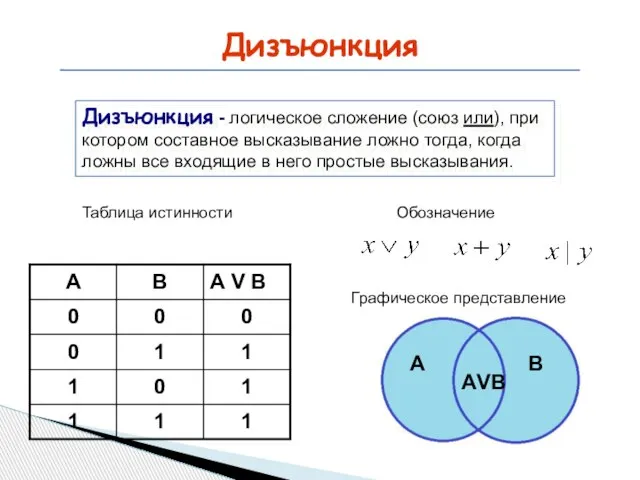
- 13. Дизъюнкция Дизъюнкция - логическое сложение (союз или), при котором составное высказывание ложно тогда, когда ложны все
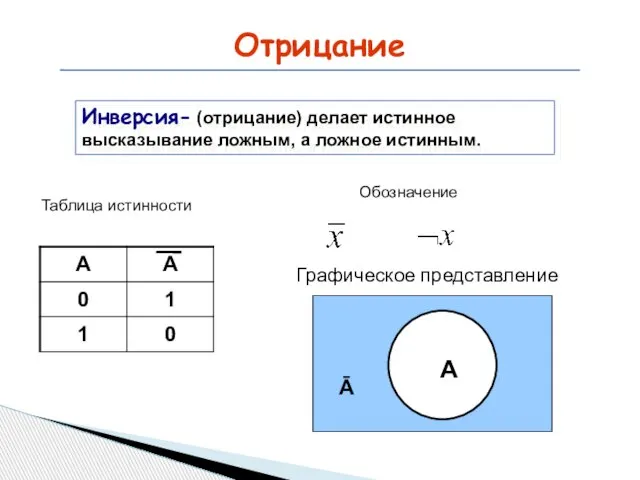
- 14. Отрицание Инверсия- (отрицание) делает истинное высказывание ложным, а ложное истинным. Таблица истинности Обозначение Графическое представление A
- 15. Импликация Импликация - (логическое следование - если…, то…). Ложно тогда и только тогда, когда из истинного
- 16. Даны два простых высказывания: А = {2 • 2 = 4}, В = {2 • 2
- 17. Задания А = «Сейчас нет дождя» В = «Форточка закрыта» Составить сложные высказывания A Λ B
- 18. Построение таблиц истинности подсчитать n - число переменных в выражении подсчитать общее число логических операций в
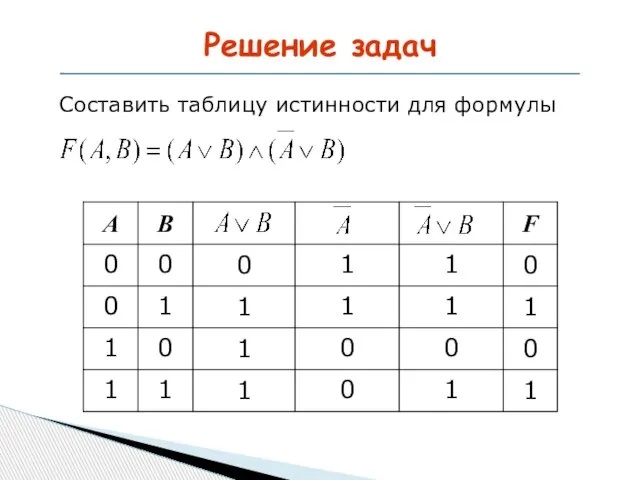
- 19. Решение задач Составить таблицу истинности для формулы
- 20. Решение задач Составить таблицу истинности для формулы
- 21. Решение задач x y Составить таблицу истинности для формулы
- 22. Напишите наименьшее число x, для которого истинно высказывание: (x > 23) И НЕ (x делится на
- 23. Напишите наименьшее число x, для которого истинно высказывание: (x > 16) И НЕ (в числе x
- 24. Напишите наименьшее число x, для которого истинно высказывание: (x > 45) И НЕ (сумма цифр числа
- 25. Напишите наибольшее число x, для которого истинно высказывание: (x
- 26. Напишите наибольшее число x, для которого истинно высказывание: НЕ (x > 31) И НЕ (x нечётное)
- 27. Задание x y Составить таблицу истинности
- 29. Скачать презентацию





















 Анализ онлайн-ресурсов для создания мультимедийных макетов
Анализ онлайн-ресурсов для создания мультимедийных макетов Понятие ИТ и ИС
Понятие ИТ и ИС Хранение информации
Хранение информации Приложение STEmnt. Проект
Приложение STEmnt. Проект Инструкция по работе в Microsoft Teams
Инструкция по работе в Microsoft Teams Мир без интернета
Мир без интернета 7-1-3 Всемирная паутина
7-1-3 Всемирная паутина ServiceDesk Plus Proqramının Təqdimatı
ServiceDesk Plus Proqramının Təqdimatı Системы счисления. Обобщение
Системы счисления. Обобщение Видиоуроки по созданию сайтов, баннеров, электронных книг
Видиоуроки по созданию сайтов, баннеров, электронных книг Графы. Кратчайшие пути
Графы. Кратчайшие пути Программирование. Рекомендации по лабораторной работе №5
Программирование. Рекомендации по лабораторной работе №5 Информационные системы
Информационные системы Информационная система ТРК
Информационная система ТРК Язык запрос SQL
Язык запрос SQL Media – средства массовой информации
Media – средства массовой информации Макетирование с помощью таблиц
Макетирование с помощью таблиц Основы PowerShell
Основы PowerShell Безопасный интернет
Безопасный интернет Цифровое будущее
Цифровое будущее Анализ сетей массового обслуживания с положительными и отрицательными заявками
Анализ сетей массового обслуживания с положительными и отрицательными заявками Всемирная паутина как информационное хранилище
Всемирная паутина как информационное хранилище Особенности алгоритма CDA в акциях
Особенности алгоритма CDA в акциях Модель и моделирование. 9 класс
Модель и моделирование. 9 класс Как подать заявку на проект Министерство школьной моды РДШ
Как подать заявку на проект Министерство школьной моды РДШ Обработка данных
Обработка данных Як пісаць для інтэрнэта
Як пісаць для інтэрнэта Микроядро Mach. ОС на его основе
Микроядро Mach. ОС на его основе