Задачи связности и реберной двусвязности на динамически меняющихся графах

Основные понятия
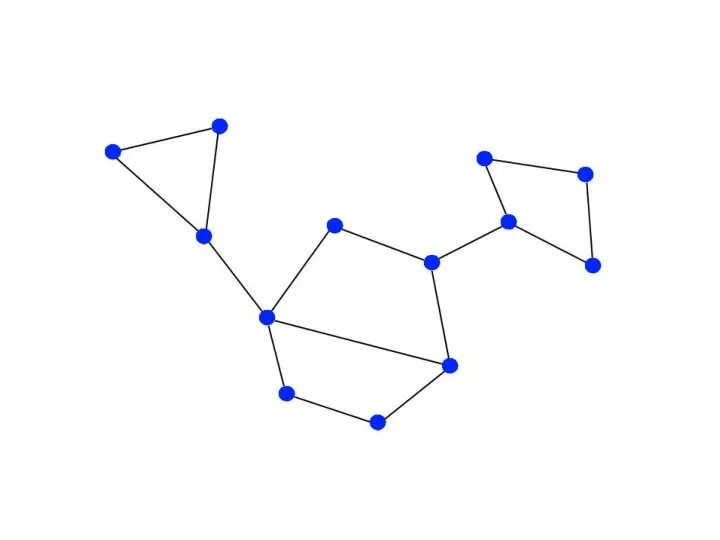
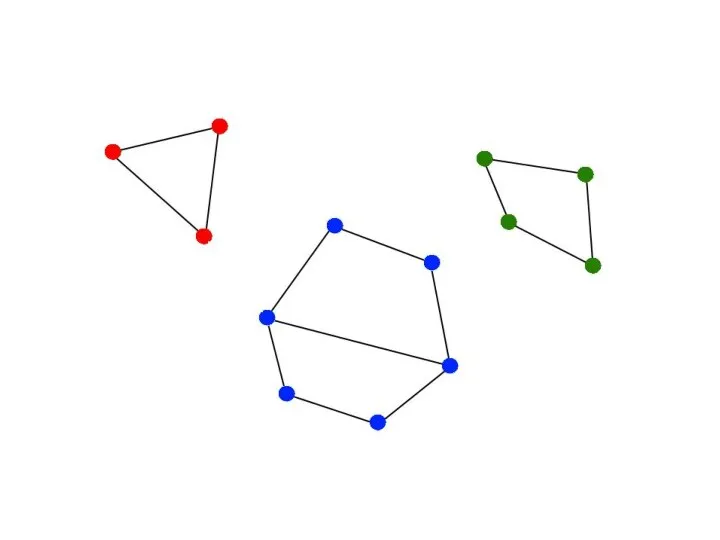
Неориентированный граф
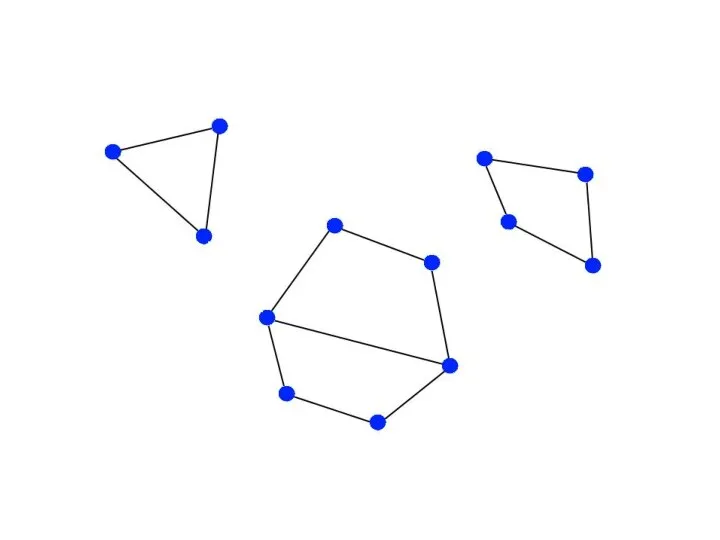
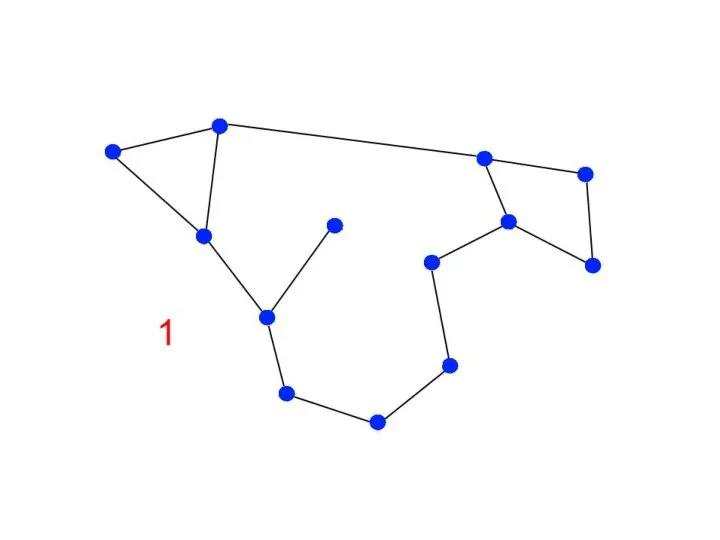
Компоненты связности
Компоненты реберной
двусвязности – вершины в одной компоненте, если существует два реберно непересекающихся пути между ними.
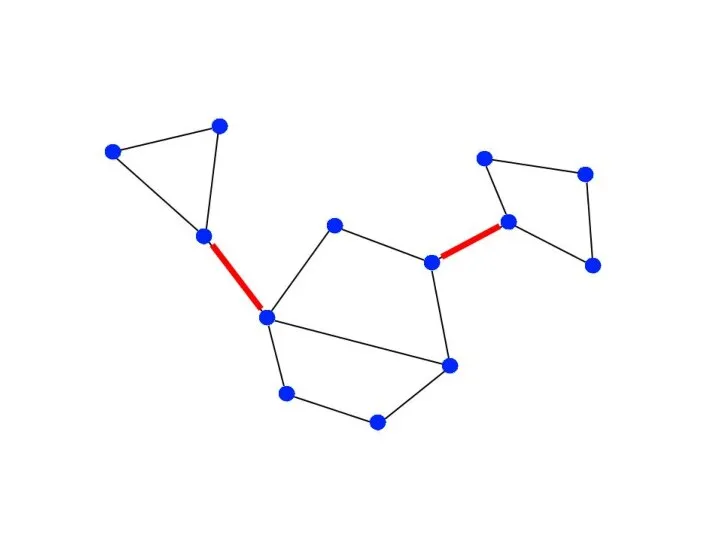
Мосты – ребра, при удалении которых увеличивается количество компонент связности.

Offline и Online
Offline задача
Все запросы к структуре данных известны заранее. Порядок запросов также известен.
Online задача
Новый запрос становится известен только после того, как на предыдущий запрос дан ответ.

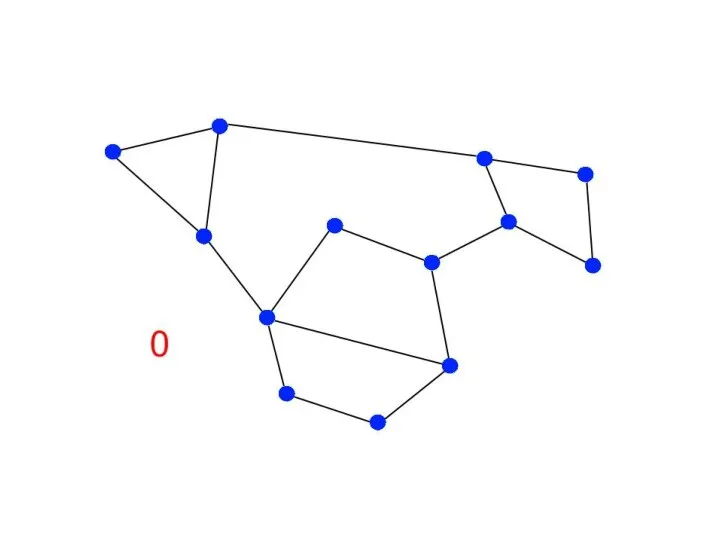
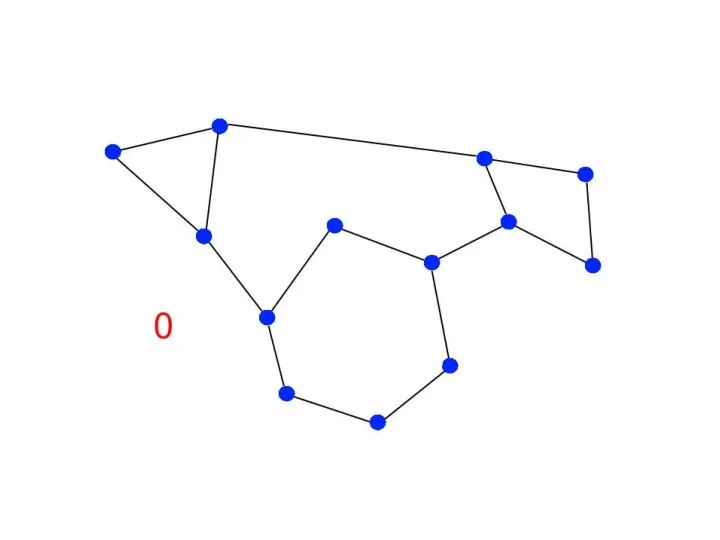
Постановка задачи связности
Неориентированный граф
Запрос изменения графа – добавить ребро или удалить ребро
Нужно после каждого запроса знать
количество компонент связности
Входные данные: изначально пустой граф и K запросов изменения графа
Выходные данные: K чисел – количество компонент связности после каждого из запросов

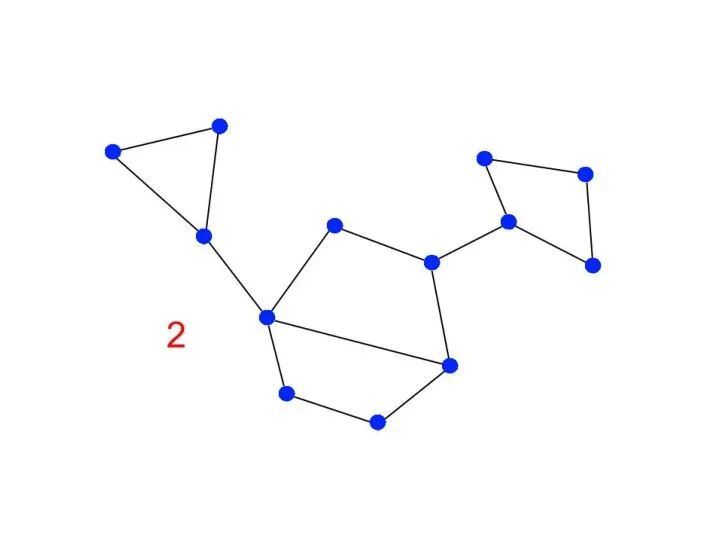
Постановка задачи двусвязности
Отличие от предыдущей задачи заключается в том, что теперь нас интересует количество
компонент реберной двусвязности и количество мостов

Усложненная задача
Между запросами изменения графа нужно обрабатывать запросы вида «лежат ли вершины A и B в одной компоненте связности», «лежат ли вершины A и B в одной компоненте реберной двусвязности, сколько между ними мостов»

Цели данной работы
Обзор существующих решений сформулированных задач.
Подробное описание известных мне offline решений обеих задач.
Разработка нового, более быстрого, offline решения.

Наивное решение
Для каждого из K моментов времени запустим процедуру поиска компонент связности и реберной двусвязности.
Время работы такого
алгоритма = O(K2). Алгоритм использует O(K) дополнительной памяти.
Обе оценки в худшем случае достигаются.

Существующие решения
Задача о связности решена в 1992-м году Eppstein-ом за время O(N * logN).
Задача о двусвязности решена Thorup-ом за время O(N * log3N * loglogN) в 2000-м году.
До сих пор это было лучшим достижением.

Основные идеи решения
Add + Delete = отрезок времени
Метод разделяй и властвуй
Можно разбить все моменты времени на две части. Рекурсивно обработать сперва первую половину, затем вторую.
Редукция и конденсация.
Если количество запросов = k, граф всегда можно уменьшить до размера O(k) вершин

Тестирование алгоритма
Реализованы 2 более медленных и простых решения.
Написаны различные генераторы
1. случайные процесс (центрированный и нет)
2. волны (длинные, короткие)
3. клики
4. циклы
5. ….
Сравнение результатов работы решений в «бесконечном» цикле.
Подсчет времени работы (реального + счетчики внутри программы).

Результат работы
Алгоритм, решающий задачу про
двусвязность за время O(KlogK)
и использующий O(K) памяти.
На Intel Pentium U5400 1.2 GHz за 1 секунду
обрабатывается более 2.105 запросов.
Подробное описание на русском языке offline решений задачи о связности

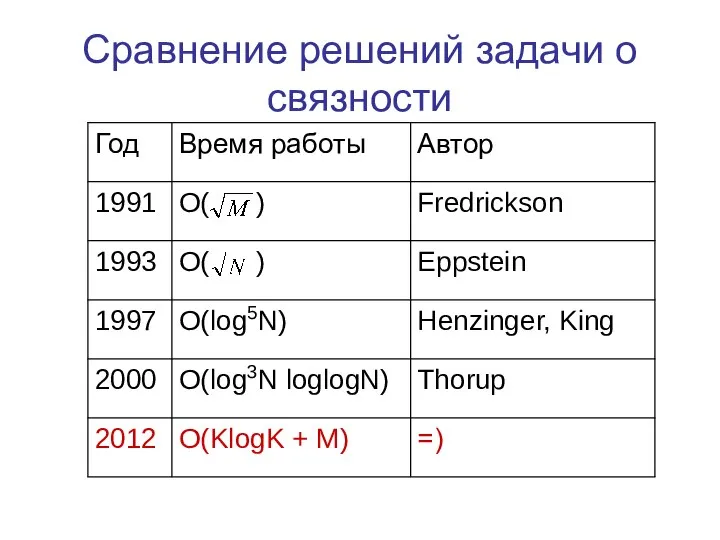
Сравнение решений задачи о связности

Сравнение решений задачи о двусвязности
Задача о связности решена в 1992-м году Eppstein-ом за время O(N * logN).
Мое решение работает за то же время.
В сравнении с решением Thorup-а, мое решение проще в реализации (у Thorup-а поддерживается MST во взвешенном меняющемся графе, а задача связности сводится к MST).

Результат 2
Эффективная реализации предложенного мной алгоритма для задачи о двусвязности.
ACM версия задачи о двусвязности (набор тестов в формате, позволяющем автоматическую проверку решений)
Аналогичный алгоритм для
задачи о связности. Требуемые время и память те же – O(KlogK) и O(K)

Применение алгоритмов
Статистические запросы к динамически меняющимся графам.
Пример #1: есть граф пользователей социальной сети, можно для фиксированной группы из K человек узнать “интересные моменты времени”, когда появлялась связность и двусвязность в данной группе.
Пример #2: Проверка надежности сетей за счет проверки того, что сеть постоянно двусвязна.