Слайд 2СОДЕРЖАНИЕ
1.1.3 Методы измерения количества информации: вероятностный и алфавитный
1.1.7 Представление числовой информации. Сложение

и умножение в разных системах счисления
Слайд 3МЕТОДЫ ИЗМЕРЕНИЯ КОЛИЧЕСТВА ИНФОРМАЦИИ:
ВЕРОЯТНОСТНЫЙ И АЛФАВИТНЫЙ
Табло состоит из светодиодов, каждый из

которых может находиться в двух состояниях («горит» или «не горит»). Какое наименьшее количество светодиодов должно находиться на табло, чтобы с его помощью можно было отобразить 130 различных сигналов?
(Сафронов И.К. Готовимся к ЕГЭ. Информатика. – 2-е изд., перераб. и доп. – СПБ.: БХВ-Петербург, 2009, стр. 4)
1) 130 2) 128 3) 13 4) 8
Решение: C помощью n светодиодов, каждый из которых может находиться в двух состояниях, можно отобразить 2n сигналов. 27 < 130 < 28, поэтому семи светодиодов недостаточно, а восьми хватит.
Ответ: 4.
Слайд 4МЕТОДЫ ИЗМЕРЕНИЯ КОЛИЧЕСТВА ИНФОРМАЦИИ:
ВЕРОЯТНОСТНЫЙ И АЛФАВИТНЫЙ
Одна ячейка памяти «троичной ЭВМ» (компьютера,

основанного на использовании троичной системы счисления) может принимать одно из трех возможных состояний. Для хранения некоторой величины отвели 4 ячейки памяти. Сколько различных значений может принимать эта величина?
(Единый государственный экзамен 2009. Информатика. Универсальные материалы для подготовки учащихся/ Под редакцией В.Р. Лещинера/ ФИПИ. – М.: Интеллект-Центр, 2009, стр. 51)
1) 12 2) 16 3) 64 4) 81
Решение: Имеем три символа и четыре разряда. По формуле N = Xi, где N – количество различных последовательностей, Х – количество символов, i - длина последовательности (или количество разрядов). Получим: N = 34 = 81.
Ответ: 4.
Слайд 5МЕТОДЫ ИЗМЕРЕНИЯ КОЛИЧЕСТВА ИНФОРМАЦИИ:
ВЕРОЯТНОСТНЫЙ И АЛФАВИТНЫЙ
В1. Одна ячейка памяти «троичной ЭВМ»

(компьютера, основанного на использовании троичной системы счисления) может принимать одно из трех возможных состояний. Для хранения некоторой величины отвели 6 ячеек памяти. Сколько различных значений может принимать эта величина?
(Единый государственный экзамен 2009. Информатика. Универсальные материалы для подготовки учащихся/ Под редакцией В.Р. Лещинера/ ФИПИ. – М.: Интеллект-Центр, 2009, стр. 98)
Решение: Имеем три символа и шесть разрядов. По формуле N = Xi, где N – количество различных последовательностей, Х – количество символов, i - длина последовательности (или количество разрядов). Получим: N = 36 = 729.
Ответ: 729.
Слайд 6МЕТОДЫ ИЗМЕРЕНИЯ КОЛИЧЕСТВА ИНФОРМАЦИИ:
ВЕРОЯТНОСТНЫЙ И АЛФАВИТНЫЙ
В1. Для передачи сигналов на флоте

используются специальные сигнальные флаги, вывешиваемые в одну линию (последовательность важна). Какое количество различных сигналов может передать корабль при помощи двух сигнальных флагов, если на корабле имеются флаги шести различных видов (флагов каждого вида неограниченное количество)?
(Единый государственный экзамен 2009. Информатика. Универсальные материалы для подготовки учащихся/ Под редакцией В.Р. Лещинера/ ФИПИ. – М.: Интеллект-Центр, 2009, стр. 106)
Решение: Имеем флаги шести различных видов и два флага для передачи сигнала. По формуле N = Xi, где N – количество различных сигналов, Х – количество флагов различного вида, i – количество флагов для передачи сигнала. Получим: N = 62 = 36.
Ответ: 36.
Слайд 7МЕТОДЫ ИЗМЕРЕНИЯ КОЛИЧЕСТВА ИНФОРМАЦИИ:
ВЕРОЯТНОСТНЫЙ И АЛФАВИТНЫЙ
Сколько существует различных последовательностей из символов

«+» и «-», длиной ровно в шесть символов?
(Единый государственный экзамен 2009. Информатика. Универсальные материалы для подготовки учащихся/ Под редакцией В.Р. Лещинера/ ФИПИ. – М.: Интеллект-Центр, 2009, стр. 9)
Решение: Имеем два символа и шесть разрядов. По формуле N = Xi, где N – количество различных последовательностей, Х – количество символов, i - длина последовательности (или количество разрядов). Получим: N = 26 = 64.
Ответ: 64.
Слайд 8МЕТОДЫ ИЗМЕРЕНИЯ КОЛИЧЕСТВА ИНФОРМАЦИИ:
ВЕРОЯТНОСТНЫЙ И АЛФАВИТНЫЙ
Сколько существует различных последовательностей из символов

«а» и «б», длиной ровно в десять символов?
(Единый государственный экзамен 2009. Информатика. Универсальные материалы для подготовки учащихся/ Под редакцией В.Р. Лещинера/ ФИПИ. – М.: Интеллект-Центр, 2009, стр. 51)
1) 20 2) 100 3) 1024 4) 2048
Решение: Имеем два символа и десять разрядов. По формуле N = Xi, где N – количество различных последовательностей, Х – количество символов, i - длина последовательности (или количество разрядов). Получим: N = 210 = 1024.
Ответ: 3.
Слайд 9МЕТОДЫ ИЗМЕРЕНИЯ КОЛИЧЕСТВА ИНФОРМАЦИИ:
ВЕРОЯТНОСТНЫЙ И АЛФАВИТНЫЙ
Сколько существует различных последовательностей из символов

«плюс» и «минус», длиной ровно в пять символов?
(Единый государственный экзамен 2009. Информатика. Универсальные материалы для подготовки учащихся/ Под редакцией В.Р. Лещинера/ ФИПИ. – М.: Интеллект-Центр, 2009, стр. 51)
1) 64 2) 50 3) 32 4) 20
Решение: Имеем два символа и пять разрядов. По формуле N = Xi, где N – количество различных последовательностей, Х – количество символов, i - длина последовательности (или количество разрядов). Получим: N = 25 = 32.
Ответ: 3.
Слайд 10МЕТОДЫ ИЗМЕРЕНИЯ КОЛИЧЕСТВА ИНФОРМАЦИИ:
ВЕРОЯТНОСТНЫЙ И АЛФАВИТНЫЙ
Азбука Морзе позволяет кодировать символы для

радиосвязи, задавая комбинацию точек и тире. Сколько различных символов (цифр, букв, знаков пунктуации и т.д.) можно закодировать используя код Морзе длиной не менее трех и не более пяти сигналов (точек и тире)?
(Единый государственный экзамен 2009. Информатика. Универсальные материалы для подготовки учащихся/ Под редакцией В.Р. Лещинера/ ФИПИ. – М.: Интеллект-Центр, 2009, стр. 51)
12 2) 56 3) 84 4) 256
Решение: У нас имеется для кодирования всего два символа – точка и тире (аналог 0 и 1 в компьютере). Количество возможных различных комбинаций из Х символов по i разрядов считается по формуле N = Xi. Таким образом, кодируем двумя символами три разряда и получаем 23 = 8 символов, кодируем двумя символами четыре разряда и получаем 24 = 16 символов, кодируем двумя символами пять разрядов и получаем 25 = 32 символа. Общее количество, таким образом, равно 8 + 16 + 32 = 56.
Ответ: 2.
Слайд 11МЕТОДЫ ИЗМЕРЕНИЯ КОЛИЧЕСТВА ИНФОРМАЦИИ:
ВЕРОЯТНОСТНЫЙ И АЛФАВИТНЫЙ
Азбука Морзе позволяет кодировать символы для

радиосвязи, задавая комбинацию точек и тире. Сколько различных символов (цифр, букв, знаков пунктуации и т.д.) можно закодировать используя код Морзе длиной не менее пяти и не более шести сигналов (точек и тире)?
(Единый государственный экзамен 2009. Информатика. Универсальные материалы для подготовки учащихся/ Под редакцией В.Р. Лещинера/ ФИПИ. – М.: Интеллект-Центр, 2009, стр. 53)
80 2) 120 3) 112 4) 96
Решение: У нас имеется для кодирования всего два символа – точка и тире (аналог 0 и 1 в компьютере). Количество возможных различных комбинаций из Х символов по i разрядов считается по формуле N = Xi. Таким образом, кодируем двумя символами пять разрядов и получаем 25 = 32 символа, кодируем двумя символами шесть разрядов и получаем 26 = 64 символа. Общее количество, таким образом, равно 32 + 64 = 96.
Ответ: 4.
Слайд 12МЕТОДЫ ИЗМЕРЕНИЯ КОЛИЧЕСТВА ИНФОРМАЦИИ:
ВЕРОЯТНОСТНЫЙ И АЛФАВИТНЫЙ
В алфавите языка планеты «Триумвират» всего

три символа – 0, 1, 2. Каждое слово состоит из трех символов. Какое максимальное количество слов возможно в этом языке?
(Сафронов И.К. Готовимся к ЕГЭ. Информатика. – 2-е изд., перераб. и доп. – СПБ.: БХВ-Петербург, 2009, стр. 10)
9 2) 24 3) 27 4) 36
Решение: По формуле количества перестановок N = Xi, где N – возможное количество перестановок (т.е. максимально допустимое количество слов), Х – количество используемых символов, i – длина слова, имеем: 33 = 27 слов возможно в этом языке.
Ответ: 3.
Слайд 13МЕТОДЫ ИЗМЕРЕНИЯ КОЛИЧЕСТВА ИНФОРМАЦИИ:
ВЕРОЯТНОСТНЫЙ И АЛФАВИТНЫЙ
У племени «чичевоков» в алфавите 24

буквы и 8 цифр и больше ничего – ни знаков препинания, ни арифметических знаков. Сколько разрядов минимум им необходимо для кодирования всех символов при помощи только нулей и единиц, используя для кодировки каждого символа одинаковое количество разрядов? Учтите, что слова надо отделять друг от друга!
(Сафронов И.К. Готовимся к ЕГЭ. Информатика. – 2-е изд., перераб. и доп. – СПБ.: БХВ-Петербург, 2009, стр. 7)
5 2) 6 3) 7 4) 8
Решение: Посчитаем, сколько всего символов надо закодировать. Получаем 24 + 8 = 32. Помня про формулу N = Xi, и то, что в нашем случае N = 32, а Х = 2, находим количество разрядов. Оно равно 5. Но слова нужно еще и отделять друг от друга пробелом, а это еще один символ. Поэтому в пять разрядов не уложиться, придется задействовать и шестой.
Ответ: 2.
Слайд 14МЕТОДЫ ИЗМЕРЕНИЯ КОЛИЧЕСТВА ИНФОРМАЦИИ:
ВЕРОЯТНОСТНЫЙ И АЛФАВИТНЫЙ
В детской игре «Угадай число» первый

участник загадал число в интервале от 1 до 64. Какое минимальное число попыток должен сделать второй участник, чтобы наверняка отгадать число, если первый участник на заявленное число второго должен только отвечать «Мое число больше», «Мое число меньше» или «Угадано»?
(Сафронов И.К. Готовимся к ЕГЭ. Информатика. – 2-е изд., перераб. и доп. – СПБ.: БХВ-Петербург, 2009, стр. 9)
1 2) 6 3) 10 4) 64
Решение: Правильная математическая стратегия такой игры – половинное деление. Число 64 = 26, значит, минимальное количество попыток, чтобы наверняка угадать число, нужно 6.
Ответ: 2.
Слайд 15МЕТОДЫ ИЗМЕРЕНИЯ КОЛИЧЕСТВА ИНФОРМАЦИИ:
ВЕРОЯТНОСТНЫЙ И АЛФАВИТНЫЙ
Задача. В языке племени Мумбо-Юмбо всего

20 разных слов. Сколько бит нужно, чтобы закодировать любое из этих слов?
Решение.
По условию задачи у нас имеется 20 различных вариантов. Применим формулу N = Xi . Заметим, что 24 < 20 < 25, поэтому 4-х бит недостаточно, а пяти хватит, т. е. , чтобы закодировать любое слово необходимо 5 бит.
Ответ: 5 бит.
Задача. В доме 14 окон. Сколько различных сигналов можно подать, зажигая свет в окнах? Сколько бит информации несет в себе каждый такой сигнал?
Решение.
Каждое окно несет в себе 1 бит информации: горит - не горит.
Количество различных равновероятных сигналов, передаваемое с помощью 14 бит равно 214 = 16 384. Каждый из 16 384 сигналов несет в себе 14 бит информации.
Ответ: 16 384 сигнала; 14 бит.
Слайд 16МЕТОДЫ ИЗМЕРЕНИЯ КОЛИЧЕСТВА ИНФОРМАЦИИ:
ВЕРОЯТНОСТНЫЙ И АЛФАВИТНЫЙ
Задача. Одиннадцать одноклассников решают голосованием, куда

пойти после уроков. При голосовании каждый может быть либо “за” либо “против”. Сколько различных вариантов голосования может быть? Сколько бит потребуется, чтобы закодировать результаты голосования?
Решение.
Каждый ответ одного из одноклассников при голосовании несет в себе 1 бит информации: «за», «против». Количество различных равновероятных ответов, передаваемых с помощью 11 бит равно 211 = 2048. Каждый из 2048 ответов несет в себе 11 бит информации.
Ответ: 2048 ответов; 11 бит.
Задача. Друзья в соседних домах договорились передавать друг другу сообщения в виде световых сигналов. Сколько лампочек им понадобиться для кодирования 10 различных слов?
Решение.
По условию задачи у нас имеется 10 различных слов. Применим формулу N = Xi .
Заметим, что 23 < 10 < 24, поэтому трех лампочек недостаточно, а четырех хватит, т. е. , чтобы закодировать 10 различных слов необходимо 4 лампочки.
Ответ: 4.
Слайд 17МЕТОДЫ ИЗМЕРЕНИЯ КОЛИЧЕСТВА ИНФОРМАЦИИ:
ВЕРОЯТНОСТНЫЙ И АЛФАВИТНЫЙ
Задача. В компьютерной игре распознаются 65

различных команд управления. Сколько бит требуется отвести в блоке памяти для кодирования каждой команды? Достаточно ли отведенных бит для кодирования 100 команд?
Решение.
По условию задачи у нас имеется 65 различных команд управления. Применим формулу N = Xi .
Заметим, что 26 < 65 < 27, поэтому шести бит недостаточно, а семи хватит, т. е. в блоке памяти для кодирования каждой команды управления надо отвести 7 бит. Так как 27 = 128 и 128 > 100. то отведенных 7 бит достаточно для кодирования 100 команд.
Ответ: 7 бит; достаточно.
Задача. Объем сообщения 7,5 Кбайт. Известно, что данное сообщение содержит 7680 символов. Какова мощность алфавита?
1) 76 2) 256 3) 156 4) 512
Решение: Переведем информационный объем сообщения в биты: 7,5 Кбайт = (7,5 ⋅ 1024 ⋅ 8) бит = 61 440 бит.
Подсчитаем количество бит для кодирования одного символа: I = 61 440 : 7 680 = 8 бит.
Тогда мощность алфавита (количество символов в алфавите) равна: N = 2I = 28 = 256.
Ответ: 2.
Слайд 18МЕТОДЫ ИЗМЕРЕНИЯ КОЛИЧЕСТВА ИНФОРМАЦИИ:
ВЕРОЯТНОСТНЫЙ И АЛФАВИТНЫЙ
Задача. Какое максимальное количество бит потребуется

для кодирования целых положительных чисел меньших 60?
1) 1 2) 6 3) 36 4) 60
Решение. Сначала решим вопрос о том, сколько двоичных разрядов понадобится для кодирования ближайшего к 60 числа, являющегося степенью числа 2 и расположенного на числовой оси справа от него. Очевидно, это число 64. Далее 64 = 26. Поэтому для его кодирования понадобится 6 бит, следовательно для кодирования целых положительных чисел меньших 60, понадобится не более 6 бит.
Ответ: 2.
Задача. Объем сообщения, содержащего 4096 символов составил 1/512 часть Мбайта. Какова мощность алфавита, с помощью которого записано это сообщение?
1) 8 2) 16 3) 4096 4) 16384
Решение: Переведем информационный объем сообщения в биты:
1/512 часть Мбайта = (1/512 ⋅ 1024 ⋅ 1024 ⋅ 8) бит = 16 384 бит.
Подсчитаем количество бит для кодирования одного символа: I = 16 384 : 4096= 4 бита.
Тогда мощность алфавита (количество символов в алфавите) равна: N = 2I = 24 = 16.
Ответ: 2.
Слайд 19ПРЕДСТАВЛЕНИЕ ЧИСЛОВОЙ ИНФОРМАЦИИ.
СЛОЖЕНИЕ И УМНОЖЕНИЕ В РАЗНЫХ СИСТЕМАХ СЧИСЛЕНИЯ
А3. Сколько единиц
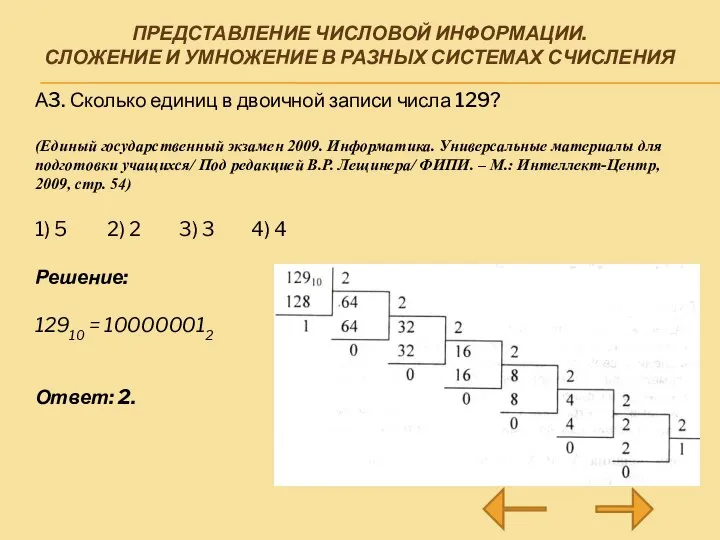
в двоичной записи числа 129?
(Единый государственный экзамен 2009. Информатика. Универсальные материалы для подготовки учащихся/ Под редакцией В.Р. Лещинера/ ФИПИ. – М.: Интеллект-Центр, 2009, стр. 54)
1) 5 2) 2 3) 3 4) 4
Решение:
12910 = 100000012
Ответ: 2.
Слайд 20ПРЕДСТАВЛЕНИЕ ЧИСЛОВОЙ ИНФОРМАЦИИ.
СЛОЖЕНИЕ И УМНОЖЕНИЕ В РАЗНЫХ СИСТЕМАХ СЧИСЛЕНИЯ
А3. Дано: а

= 9216, b = 2248. Какое из чисел c, записанных в двоичной системе, отвечает условию a < c < b?
(Единый государственный экзамен 2009. Информатика. Универсальные материалы для подготовки учащихся/ Под редакцией В.Р. Лещинера/ ФИПИ. – М.: Интеллект-Центр, 2009, стр. 93)
1) 10010011 2) 10001110 3) 10001010 4) 10001100
Решение:
Переводим числа в одну систему счисления, например, в десятичную:
а = 14610 b = 14810
100100112 = 14710
100011102 = 14210
100010102 = 13810
100011002 = 14010
Ответ: 1.
Слайд 21ПРЕДСТАВЛЕНИЕ ЧИСЛОВОЙ ИНФОРМАЦИИ.
СЛОЖЕНИЕ И УМНОЖЕНИЕ В РАЗНЫХ СИСТЕМАХ СЧИСЛЕНИЯ
А3. Дано: а

= 3D16, b = 778. Какое из чисел c, записанных в двоичной системе, отвечает условию a < c < b?
(Единый государственный экзамен 2009. Информатика. Универсальные материалы для подготовки учащихся/ Под редакцией В.Р. Лещинера/ ФИПИ. – М.: Интеллект-Центр, 2009, стр. 102)
1) 111101 2) 111110 3) 111111 4) 111010
Решение:
Переводим числа в одну систему счисления, например, в десятичную:
а = 6110 b = 6310
1111012 = 6110
1111102 = 6210
1111112 = 6310
1110102 = 5810
Ответ: 2.
Слайд 22ПРЕДСТАВЛЕНИЕ ЧИСЛОВОЙ ИНФОРМАЦИИ.
СЛОЖЕНИЕ И УМНОЖЕНИЕ В РАЗНЫХ СИСТЕМАХ СЧИСЛЕНИЯ
А3. Число 5678

запишите в двоичной системе счисления.
1) 1011101 2) 100110111 3) 101110111 4) 11110111
Решение:
Переводим число 5678 сначала в десятичную систему счисления, а потов двоичную: 5678 = 37510 = 1011101112
Ответ: 3.
А3. Сколько единиц содержится в двоичной записи десятичного числа 173?
1) 4 2) 5 3) 6 4) 7
Решение: 17310 = 101011012
Ответ: 2.
Слайд 23ПРЕДСТАВЛЕНИЕ ЧИСЛОВОЙ ИНФОРМАЦИИ.
СЛОЖЕНИЕ И УМНОЖЕНИЕ В РАЗНЫХ СИСТЕМАХ СЧИСЛЕНИЯ
А3. Какое число
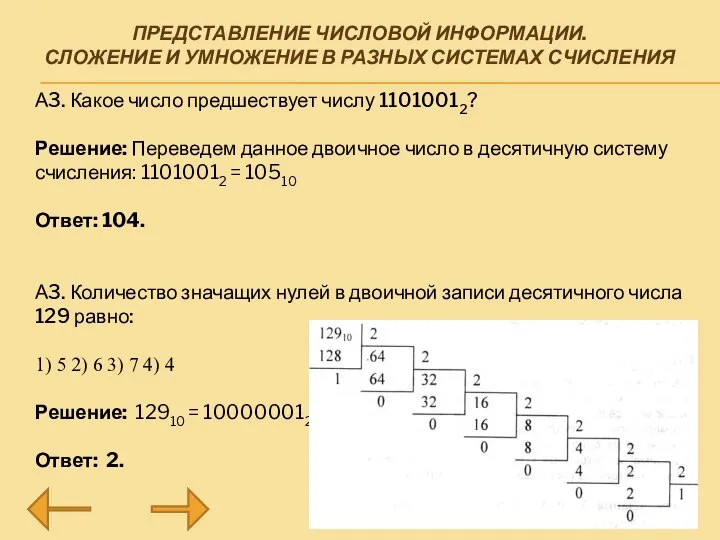
предшествует числу 11010012?
Решение: Переведем данное двоичное число в десятичную систему счисления: 11010012 = 10510
Ответ: 104.
А3. Количество значащих нулей в двоичной записи десятичного числа 129 равно:
1) 5 2) 6 3) 7 4) 4
Решение: 12910 = 100000012
Ответ: 2.
Слайд 24ПРЕДСТАВЛЕНИЕ ЧИСЛОВОЙ ИНФОРМАЦИИ.
СЛОЖЕНИЕ И УМНОЖЕНИЕ В РАЗНЫХ СИСТЕМАХ СЧИСЛЕНИЯ
А4. Чему равна

сумма 578 и 4616?
(Единый государственный экзамен 2009. Информатика. Универсальные материалы для подготовки учащихся/ Под редакцией В.Р. Лещинера/ ФИПИ. – М.: Интеллект-Центр, 2009, стр. 102)
10101012 2) 1258 3) А316 4) 7516
Решение: Переведем числа в десятичную систему счисления:
578 = 4710 4616 = 7010
Найдем их сумму: 4710 + 7010 = 11710
Переведем полученную сумму в 16-ую систему счисления: 11710 = 7516
Ответ: 4.
Слайд 25ПРЕДСТАВЛЕНИЕ ЧИСЛОВОЙ ИНФОРМАЦИИ.
СЛОЖЕНИЕ И УМНОЖЕНИЕ В РАЗНЫХ СИСТЕМАХ СЧИСЛЕНИЯ
А4. Чему равна

сумма 418 и 5716?
(Единый государственный экзамен 2009. Информатика. Универсальные материалы для подготовки учащихся/ Под редакцией В.Р. Лещинера/ ФИПИ. – М.: Интеллект-Центр, 2009, стр. 93)
1208 2) 1708 3) 6816 4) 10000002
Решение: Переведем числа в десятичную систему счисления:
418 = 3310 5716 = 8710
Найдем их сумму: 3310 + 8710 = 12010
Переведем полученную сумму в 8-ую систему счисления: 12010 = 1708
Ответ: 2.
Слайд 26ПРЕДСТАВЛЕНИЕ ЧИСЛОВОЙ ИНФОРМАЦИИ.
СЛОЖЕНИЕ И УМНОЖЕНИЕ В РАЗНЫХ СИСТЕМАХ СЧИСЛЕНИЯ
А4. Чему равна

разность чисел 10116 и 11001012?
(Единый государственный экзамен 2009. Информатика. Универсальные материалы для подготовки учащихся/ Под редакцией В.Р. Лещинера/ ФИПИ. – М.: Интеллект-Центр, 2009, стр. 54)
448 2) 2348 3) 3616 4) 6016
Решение: Переведем числа в десятичную систему счисления:
10116 = 25710 11001012 = 10110
Найдем их разность: 25710 - 10110 = 15610
Переведем полученную сумму в 8-ую систему счисления: 15610 = 2348
Ответ: 2.
Слайд 27ПРЕДСТАВЛЕНИЕ ЧИСЛОВОЙ ИНФОРМАЦИИ.
СЛОЖЕНИЕ И УМНОЖЕНИЕ В РАЗНЫХ СИСТЕМАХ СЧИСЛЕНИЯ
А4. Вычислите сумму

чисел х и у, если х = 11101012 и у = 10110112. Результат представьте в виде восьмеричного числа.
(Единый государственный экзамен 2009. Информатика. Универсальные материалы для подготовки учащихся/ Под редакцией В.Р. Лещинера/ ФИПИ. – М.: Интеллект-Центр, 2009, стр. 54)
21108 2) 2988 3) 3208 4) 3188
Решение: Переведем числа в десятичную систему счисления:
11101012 = 11710 101101116 = 9110
Найдем их сумму: 11710 + 9110 = 20810
Переведем полученную сумму в 8-ую систему счисления: 20810 = 3208
Ответ: 3.
Слайд 28ПРЕДСТАВЛЕНИЕ ЧИСЛОВОЙ ИНФОРМАЦИИ.
СЛОЖЕНИЕ И УМНОЖЕНИЕ В РАЗНЫХ СИСТЕМАХ СЧИСЛЕНИЯ
А4. Вычислите сумму

двоичных чисел х и у, если х = 10101012 и
у = 10100112.
(Единый государственный экзамен 2009. Информатика. Универсальные материалы для подготовки учащихся/ Под редакцией В.Р. Лещинера/ ФИПИ. – М.: Интеллект-Центр, 2009, стр. 55)
101000102 2) 101010002 3) 101001002 4) 101110002
Решение: Найдем сумму двоичных чисел:
+ 10101012
10100112
101010002
Ответ: 2.
Слайд 29ПРЕДСТАВЛЕНИЕ ЧИСЛОВОЙ ИНФОРМАЦИИ.
СЛОЖЕНИЕ И УМНОЖЕНИЕ В РАЗНЫХ СИСТЕМАХ СЧИСЛЕНИЯ
А4. Вычислите сумму

чисел х и у, при х = В416 и у = 468. Результат представьте в двоичной системе счисления.
(Единый государственный экзамен 2009. Информатика. Универсальные материалы для подготовки учащихся/ Под редакцией В.Р. Лещинера/ ФИПИ. – М.: Интеллект-Центр, 2009, стр. 55)
110110102 2) 100000102 3) 11100102 4) 101110102
Решение: Переведем числа в десятичную систему счисления:
В416 = 18010 468 = 3810
Найдем их сумму: 18010 + 3810 = 21810
Переведем полученную сумму в 2-ую систему счисления: 21810 = 110110102
Ответ: 1.
Слайд 30ПРЕДСТАВЛЕНИЕ ЧИСЛОВОЙ ИНФОРМАЦИИ.
СЛОЖЕНИЕ И УМНОЖЕНИЕ В РАЗНЫХ СИСТЕМАХ СЧИСЛЕНИЯ
А4. Вычислите сумму

двоичных чисел х и у, при х = 1D16 и у = 728. Результат представьте в двоичной системе счисления.
(Единый государственный экзамен 2009. Информатика. Универсальные материалы для подготовки учащихся/ Под редакцией В.Р. Лещинера/ ФИПИ. – М.: Интеллект-Центр, 2009, стр. 55)
100011112 2) 11001012 3) 1010112 4) 10101112
Решение: Переведем числа в десятичную систему счисления:
1D16 = 2910 728 = 5810
Найдем их сумму: 2910 + 5810 = 8710
Переведем полученную сумму в 2-ую систему счисления: 8710 = 10101112
Ответ: 4.
Слайд 31ПРЕДСТАВЛЕНИЕ ЧИСЛОВОЙ ИНФОРМАЦИИ.
СЛОЖЕНИЕ И УМНОЖЕНИЕ В РАЗНЫХ СИСТЕМАХ СЧИСЛЕНИЯ
В3. Укажите через

запятую в порядке возрастания все основания систем счисления, в которых запись числа 16 оканчивается на 1.
(Единый государственный экзамен 2009. Информатика. Универсальные материалы для подготовки учащихся/ Под редакцией В.Р. Лещинера/ ФИПИ. – М.: Интеллект-Центр, 2009, стр. 98)
Решение:
a = bq + r, где b – делитель, q - неполное частное, r – остаток, 0 ≤ r ≤ b.
16 = bq + 1, bq = 16 – 1, bq = 15 (15 = 1? 15, 15 = 3 ? 5), {1, 3, 5, 15}.
По определению позиционной системы счисления основание P∈ N и Р > 1,
т.е. Р = 3, 5, 15.
Ответ: 3, 5, 15
Слайд 32ПРЕДСТАВЛЕНИЕ ЧИСЛОВОЙ ИНФОРМАЦИИ.
СЛОЖЕНИЕ И УМНОЖЕНИЕ В РАЗНЫХ СИСТЕМАХ СЧИСЛЕНИЯ
В3. Укажите через

запятую в порядке возрастания все основания систем счисления, в которых запись числа 24 оканчивается на 3.
(ЕГЭ 2008. Информатика. Федеральный банк экзаменационных материалов/ Авт.-сост. П.А. Якушкин, С.С. Крылов. – М.: Эксмо, стр. 13)
Решение:
a = bq + r, где b – делитель, q - неполное частное, r – остаток, 0 ≤ r ≤ b.
24 = bq + 3, bq = 24 – 3, bq = 21 (21 = 1? 21, 21 = 3 ? 7), {1, 3, 7, 21}.
По определению позиционной системы счисления основание P∈ N и Р > 1, для данного случая Р ≠ 2, 3, т.е. Р = 7, 21.
Ответ: 7, 21.
Слайд 33ПРЕДСТАВЛЕНИЕ ЧИСЛОВОЙ ИНФОРМАЦИИ.
СЛОЖЕНИЕ И УМНОЖЕНИЕ В РАЗНЫХ СИСТЕМАХ СЧИСЛЕНИЯ
В3. Укажите через

запятую в порядке возрастания все числа, не превосходящие 11, запись которых в пятеричной системе счисления начинается на 2.
(Единый государственный экзамен 2009. Информатика. Универсальные материалы для подготовки учащихся/ Под редакцией В.Р. Лещинера/ ФИПИ. – М.: Интеллект-Центр, 2009, стр. 107)
Решение: Переводим число 11 в пятеричную систему счисления:
1110 = 215
Искомые числа должны быть <= 11, значит, в их записи присутствует не более 2-х разрядов, и начинаются числа на 2. Первое искомое число – это 2.
Далее имеем: 2Х5 <= 215, получаем, что Х=0 или Х=1 в пятеричной системе. Таким образом, находим эти два числа в десятичной системе:
205 = 1010, 215 = 1110
Ответ: 2, 10, 11.
Слайд 34ПРЕДСТАВЛЕНИЕ ЧИСЛОВОЙ ИНФОРМАЦИИ.
СЛОЖЕНИЕ И УМНОЖЕНИЕ В РАЗНЫХ СИСТЕМАХ СЧИСЛЕНИЯ
В3. В системе

счисления с некоторым основанием число 17 записывается в виде 101. Укажите это основание. (Демо-версия ЕГЭ 2006)
Решение: Пусть х – основание системы счисления. Тогда, по правилам перевода числа из любой системы счисления в десятичную, запишем уравнение:
101х = 1 ⋅ х2 + 0 ⋅ х1 + 1 ⋅ х0
1710 = х2 + 1, х2 = 16, х = 4.
Ответ: 4.
Слайд 35ПРЕДСТАВЛЕНИЕ ЧИСЛОВОЙ ИНФОРМАЦИИ.
СЛОЖЕНИЕ И УМНОЖЕНИЕ В РАЗНЫХ СИСТЕМАХ СЧИСЛЕНИЯ
В3. В системе

счисления с некоторым основанием десятичное число 129 записывается как 1004. Укажите это основание.
Решение: Пусть х – основание неизвестной нам системы счисления. Тогда, по правилам перевода числа из любой системы счисления в десятичную, запишем уравнение:
1004х = 1 ⋅ х3 + 0 ⋅ х2 + 0 ⋅ х1 + 4 ⋅ х0, 12910 = х3 + 4, х3 = 125, х = 5.
Ответ: 5.


































 Методология IDEF0
Методология IDEF0 Асфальт 8. Какие машины бывают
Асфальт 8. Какие машины бывают Текст и его типы
Текст и его типы Презентация для получателей гранта
Презентация для получателей гранта Российская электронная школа
Российская электронная школа О подготовке и защите выпускных квалификационных работ на факультете прикладной информатики
О подготовке и защите выпускных квалификационных работ на факультете прикладной информатики Операционные системы
Операционные системы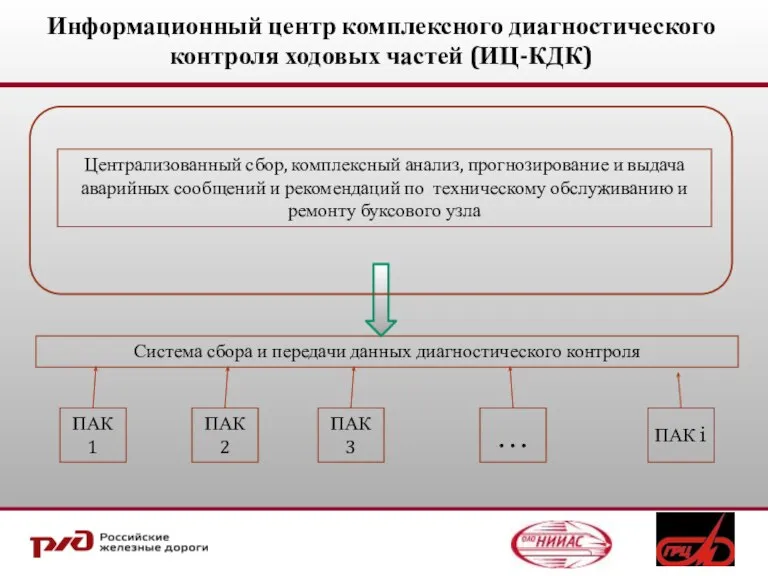 Информационный центр комплексного диагностического контроля ходовых частей (ИЦ-КДК)
Информационный центр комплексного диагностического контроля ходовых частей (ИЦ-КДК) Презентация на тему Линейные алгоритмы (4 класс)
Презентация на тему Линейные алгоритмы (4 класс)  Шрифты, списки
Шрифты, списки Программирование на языке Java. Форматный вывод
Программирование на языке Java. Форматный вывод Электронные таблицы. Основные параметры электронных таблиц
Электронные таблицы. Основные параметры электронных таблиц Массивы в Javascript
Массивы в Javascript Витраж. Алгоритм
Витраж. Алгоритм Собрание для пожертвования
Собрание для пожертвования Моделирование причёски
Моделирование причёски Графические информационные модели. К уроку информатики в 9 классе
Графические информационные модели. К уроку информатики в 9 классе Системы счисления. Непозиционные системы счисления
Системы счисления. Непозиционные системы счисления Untitled presentation (2)
Untitled presentation (2) Пазл. Откройте фотографию
Пазл. Откройте фотографию Опрос аудитории паблика OH MY HYPE
Опрос аудитории паблика OH MY HYPE Глобальная компьютерная сеть Интернет
Глобальная компьютерная сеть Интернет Электронная почта. Сетевое коллективное взаимодействие. Сетевой этикет
Электронная почта. Сетевое коллективное взаимодействие. Сетевой этикет Управление стейкхолдерами проекта. Антивирусы
Управление стейкхолдерами проекта. Антивирусы Logical gates. Логические ворота
Logical gates. Логические ворота Логические операции
Логические операции Графический редактор Photoshop
Графический редактор Photoshop Торгово-закупочные B2B системы. Отраслевая электронная торговая площадка LESPROM
Торгово-закупочные B2B системы. Отраслевая электронная торговая площадка LESPROM