Слайд 3Закон тождества. Всякое высказывание тождественно самому себе:
А=А
Закон непротиворечия. Высказывание не может быть

одновременно истинным и ложным. Если высказывание истинно, то его отрицание должно быть ложным. Значит, логическое произведение высказывания и его отрицания должно быть ложно:
Слайд 4Закон исключенного третьего. Высказывание может быть либо истинным, либо ложным, третьего не

дано. Это означает, что результат логического сложения высказывания и его отрицания всегда принимает значение «истина»:
Закон двойного отрицания. Если дважды отрицать некоторое высказывание, то в результате мы получим исходное высказывание:
Слайд 5Закон идемпотентности (от лат. слов idem – тот же самый и potens

– сильный; дословно – равносильный):
Законы исключения констант
Слайд 6Законы де Моргана
Закон коммутативности
Закон ассоциативности

Слайд 7Закон дистрибутивности
Закон поглощения
А v (А & В)=А
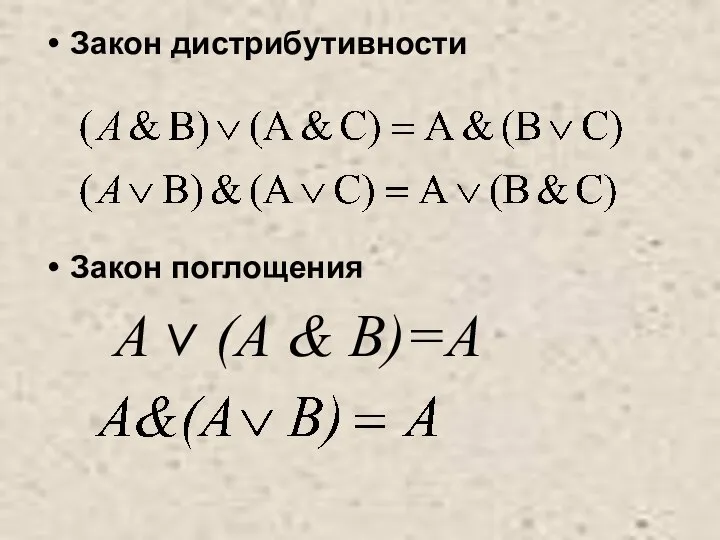
Слайд 8Законы склеивания
Закон контрапозиции (правило перевертывания)

Слайд 9Задания
Доказать справедливость 1-го и 2-го законов де Моргана, используя таблицы истинности.
Упростить логические

выражения:
Найдите Х, если





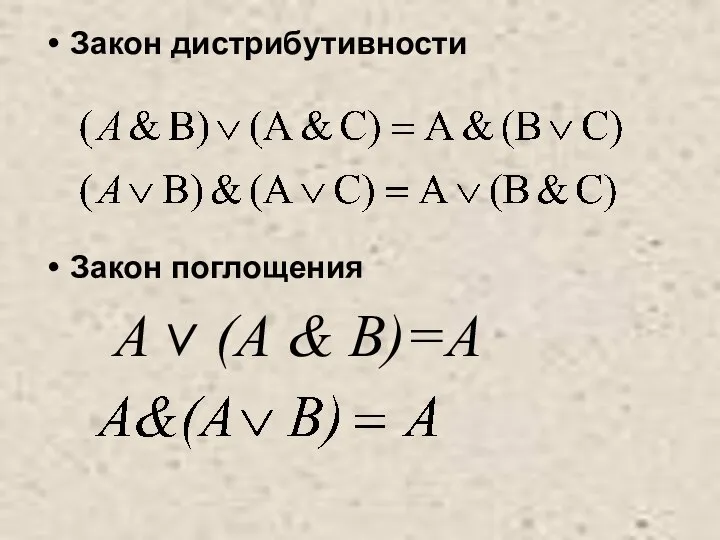


 RFID технология: Открытая библиотека
RFID технология: Открытая библиотека Что такое компьютер
Что такое компьютер Безопасность школьников в сети интернет
Безопасность школьников в сети интернет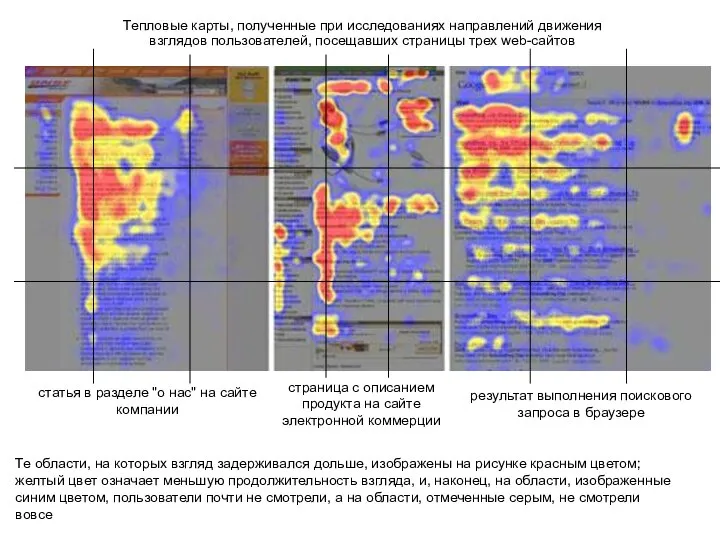 Тепловые карты, полученные при исследованиях направлений движения взглядов пользователей, посещавших страницы трех web-сайтов
Тепловые карты, полученные при исследованиях направлений движения взглядов пользователей, посещавших страницы трех web-сайтов Мульт-студия Компьюша
Мульт-студия Компьюша Pencil Code. Подфункции и тестирование
Pencil Code. Подфункции и тестирование Основы проектной деятельности. Лекция 2
Основы проектной деятельности. Лекция 2 UEFI (United Extensible Firmware Interface). Классический BIOS
UEFI (United Extensible Firmware Interface). Классический BIOS Эллиптическое шифрование
Эллиптическое шифрование Эволюция ОС
Эволюция ОС Дорожные знаки. Предписывающие знаки
Дорожные знаки. Предписывающие знаки Построение диаграмм и графиков в электронных таблицах (8 класс)
Построение диаграмм и графиков в электронных таблицах (8 класс) Короткі історичні відомості (від абака до нетбука ). 2 клас
Короткі історичні відомості (від абака до нетбука ). 2 клас Космические системы ретрансляции. Радио-ретрансляция и оптическая ретрансляция
Космические системы ретрансляции. Радио-ретрансляция и оптическая ретрансляция Автоматизированные информационные системы
Автоматизированные информационные системы Методы журналистского творчества. Методика работы с источниками информации
Методы журналистского творчества. Методика работы с источниками информации Режимы работы клиент-программы электронной почты
Режимы работы клиент-программы электронной почты Представление чисел в компьютере. Неотрицательные числа
Представление чисел в компьютере. Неотрицательные числа Развитие вычислительной техники
Развитие вычислительной техники Просмотр и редактирование жесткого диска (DiskEditor)
Просмотр и редактирование жесткого диска (DiskEditor) Анимация в Microsoft PowerPoint 2013
Анимация в Microsoft PowerPoint 2013 Построение и редактирование геометрических объектов Компас-3D
Построение и редактирование геометрических объектов Компас-3D Академия роботов. Аэроплан (airplane)
Академия роботов. Аэроплан (airplane) Авторизация и Развитие Партнеров Hewlett Packard Enterprise
Авторизация и Развитие Партнеров Hewlett Packard Enterprise Преимущества использования Mapublisher в картографии
Преимущества использования Mapublisher в картографии Библиотека им.В.И. Ленина, Санкт-Петербург
Библиотека им.В.И. Ленина, Санкт-Петербург Вплив пандемії COVID-19 на розвиток фінтеху
Вплив пандемії COVID-19 на розвиток фінтеху Неформальное введение в объектно-ориентированное программирование
Неформальное введение в объектно-ориентированное программирование