Занятие 10

Обработка сбоев аппаратуры
Возможности необходимые в программных системах для борьбы со сбоями
аппаратуры:
Повторное выполнение операций
Восстановление памяти
Динамическое изменение конфигурации
Восстановление файлов
Контрольная точка/рестарт
Предупреждение отказов питания
Регистрация ошибок

Модели надежности программного обеспечения
Модель надежности программного обеспечения относится
к математической модели, построенной для оценки
зависимости надежности программного обеспечения от
некоторых определенных параметров.
Виды модели надежности программного обеспечения:
Феноменологическая (измеряющие и оценивающие модели).
Эмпирическая (базируются на анализе структурных особенностей программ)

Модели надежности программного обеспечения
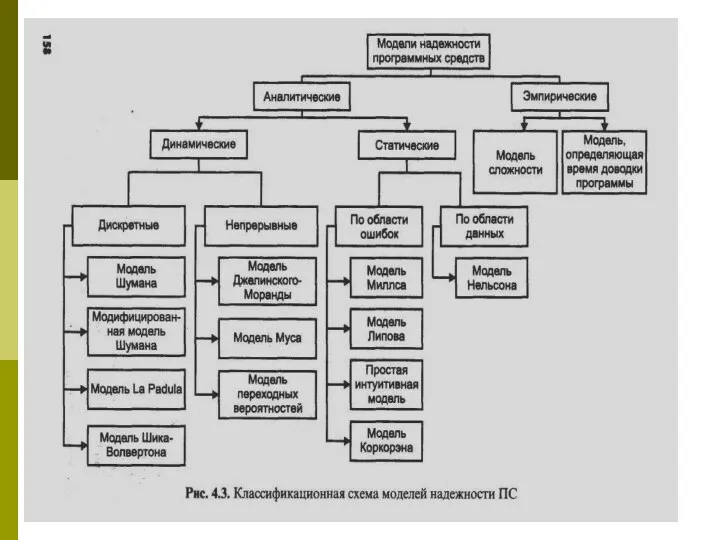
Модели надежности программных средств (МНПС) подразделяются:
Аналитические:
Динамические модели Статические модели
Эмпирические

Модели надежности программного обеспечения
Статические

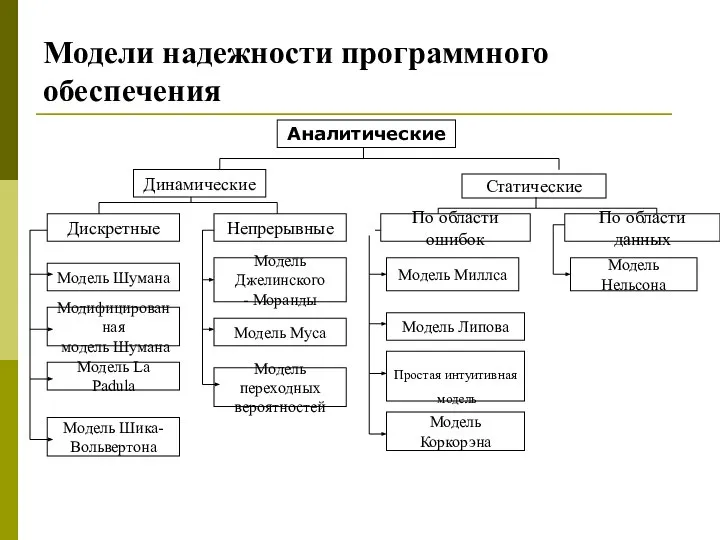
Аналитические модели надежности
Аналитические модели надежности – дают вероятность
рассчитать показатели надежности, основываясь на данных о поведении
программы в процессе тестирования.
Измерение и определение количественных показателей надежности:
Эмпирические – базируется на анализе структурных особенностей
программы (линейные разветвления программы);
Динамические – появление отказов программных средств
рассматривается во времени;
Статистические – учитывает зависимость количества ошибок от числа
тестовых прогонов или от характеристики входных данных;
Непрерывные – фиксируют число отказов за произвольный интервал времени;
Дискретные – фиксируют интервалы каждого отказа.

Аналитические модели надежности
Шаги аналитической модели надежности :
1) Определение предположений, связанных с процедурой тестирования ПС;
2) Разработка или выбор аналитической модели, базирующейся на предположениях о процедуре тестирования;
3) Выбор параметров моделей с использованием полученных
данных;
4) Применение модели — расчет количественных показателей надежности по модели.

Аналитические модели надежности
Модели:
Модель Шумана
Модель La Padula
Модель Джелинского - Моранды
Модель Шика - Волвертона
Модель Муса
Модель переходных вероятностей.
Статические модели надежности.
Модель Миллса.
Модель Липова.
Простая интуитивная модель.
Модель Коркорэна.
Модель Нельсона.

Модель Шумана
Et - количество ошибок
It - общее число машинных команд, которое предполагается постоянным в рамках
этапа тестирования.
Определяем количество ошибок на одну команду:
Значение функции частоты отказов Z(t) пропорционально числу ошибок, оставшихся в
ПС после израсходованного на тестирование времени τ:
С — некоторая константа;
t — время работы ПС без отказа

Модель Шумана
Интенсивность отказа в промежуток времени:
Ai — количество ошибок на i-м прогоне; - время за которое проведено тестирование
Количество ошибок в системе:
Коэффициент связности:

Модель Миллса.
N — первоначальное число ошибок в программе.
S — количество искусственно внесенных ошибок
n — число найденных собственных ошибок
V — число обнаруженных к моменту оценки искусственных ошибок

Модель Миллса.
Вторая часть заключается в определении вероятности того, что в
результате тестирования обнаружены все ошибки, если обнаружены все
искусственные ошибки.
Величина С является мерой доверия к модели и показывает вероятность
того, насколько правильно найдено значение N.

Эмпирические модели надежности

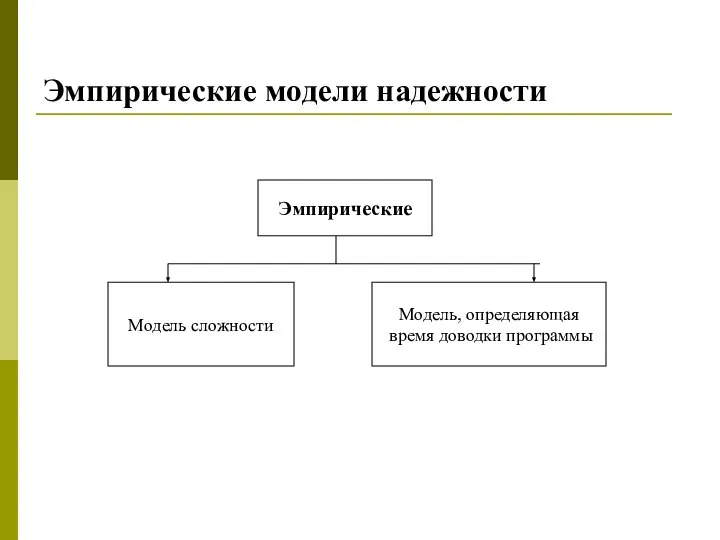
Эмпирические модели надежности
Модель сложности
В качестве структурных характеристик модуля ПС используются:
отношение действительного числа дуг к максимально возможному числу дуг, получаемому искусственным соединением
каждого узла с любым другим узлом дугой;
отношение числа узлов к числу дуг;
отношение числа петель к общему числу дуг.
оценки показателей надежности по имитационной модели, создаваемой на основе анализа структуры будущего реального ПС, заключаются в следующем:
модель позволяет на этапе проектирования ПС принимать оптимальные проектные решения, опираясь на характеристики ошибок, оцениваемые с помощью имитационной модели;
модель позволяет прогнозировать требуемые ресурсы тестирования;
модель дает возможность определить меру сложности программ
и предсказать возможное число ошибок и т.д.